これまで
にて多重積分は下記4つのパターン
1. 積分領域が定数のみで決まり、被積分関数が変数分離できる場合
2. 積分領域が定数のみで決まり、被積分関数が変数分離できない場合
3. 積分領域が変数に依存し、変数変換する必要がない場合
4. 積分領域が変数に依存し、変数変換する必要がある場合
の内の1,2,3についてに見てきた。
最後に4つ目のパターン「積分領域が変数に依存し、変数変換する必要がある場合」を扱う。
4. 積分領域が変数に依存し、変数変換する必要がある場合
今までの3パターンでは、積分領域が比較的単純だった。
しかし積分領域が複雑になると計算が煩雑になったり、そもそも与えられた座標系では解析的に積分できない場合がある。
その場合には、座標変換によって積分変数の変換を行い、積分領域を単純化した上で積分計算を進めていく。
積分変数の変換は、次のように実施する。
ある\(n\)変数関数\(f(x_{1},…,x_{n})\)を領域\(D\)にわたって積分することを考える。
\begin{align}
\int_{D}dx_{1}\cdots dx_{n}f(x_{1},…,x_{n})
\end{align}
ここで\((x_{1},…,x_{n})\to(\alpha_{1},…,\alpha_{n})\)の変数変換を実施したとき、変数変換後の領域を\(D’\)として上記の積分は
\begin{align}
&\int_{D}dx_{1}\cdots dx_{n}f(x_{1},…,x_{n})\notag \\
=&\int_{D’}\left|\frac{\partial (x_{1},…,x_{n})}{\partial (\alpha_{1},…,\alpha_{n})}\right|d\alpha_{1}\cdots d\alpha_{n}f(x_{1}(\alpha_{1},…,\alpha_{n}),x_{2}(\alpha_{1},…,\alpha_{n}),…,x_{n}(\alpha_{1},…,\alpha_{n}))
\end{align}
と書ける。
ここで登場する\(\displaystyle{\left|\frac{\partial (x_{1},…,x_{n})}{\partial (\alpha_{1},…,\alpha_{n})}\right|}\)はヤコビアンの絶対値である。
すなわち、積分変数を変換したのち、被積分関数にヤコビアンの絶対値をかければよい。
ここで例題を解きながら、具体的にどのように変数変換と積分を進めていくかを見ていく。
問題
次の定積分を求めよ。
(1) \(\displaystyle{f(x,y)=\frac{a}{(x^{2}+y^{2}+a^{2})^{3/2}},\qquad D:R_{1}^{2}\leq x^{2}+y^{2}\leq R_{2}^{2}}\)
(2) \(\displaystyle{f(x,y,z)=2z^{3}(2x^{2}-y^{2}),\qquad D:x^{2}+y^{2}+z^{2}\leq a^{2},\,z\geq 0}\)
解説
(1)
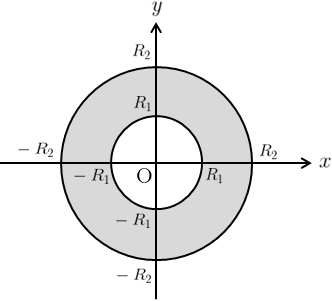
与えられた座標系では、積分領域\(D\)は図1のようにドーナツ型になる。
そこで今回は極座標系\((r,\theta)\)に座標変換する。
\begin{align}
\begin{cases}
x=r\cos\theta \\
y=r\sin\theta
\end{cases}
\qquad(R_{1}\leq r\leq R_{2},\,0\leq\theta\leq 2\pi)
\end{align}
このとき、新たな積分領域\(D’\)は図2のようになる。
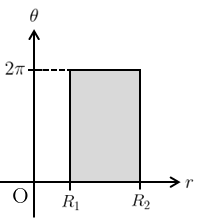
また、ヤコビアンは
\begin{align}
\frac{\partial (x,y)}{\partial (r,\theta)}=r
\end{align}
となるため、求める定積分は
\begin{align}
\iint_{D}dxdy\frac{a}{(x^{2}+y^{2}+a^{2})^{3/2}}&=\iint_{D’}\left|\frac{\partial (x,y)}{\partial (r,\theta)}\right|drd\theta\frac{a}{(r^{2}\cos^{2}\theta+r^{2}\sin^{2}\theta+a^{2})^{3/2}} \notag \\
&=\int_{R_{1}}^{R_{2}}dr\int_{0}^{2\pi}d\theta\frac{ar}{(r^{2}+a^{2})^{3/2}} \notag \\
&=2\pi a\pi\left[-\frac{1}{(r^{2}+a^{2})^{1/2}}\right]_{R_{1}}^{R_{2}} \notag \\
&=\boxed{2\pi a\left(\frac{1}{\sqrt{R_{1}^{2}-a^{2}}}-\frac{1}{\sqrt{R_{2}^{2}-a^{2}}}\right)}
\end{align}
となる。
(2)
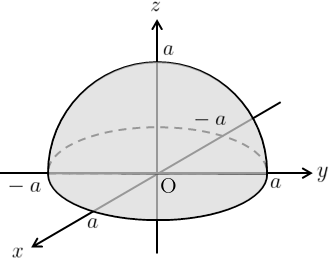
与えられた座標系では、積分領域\(D\)は図3のように半球型になる。
そこで今回は極座標系\((r,\theta,\phi)\)に座標変換する。
\begin{align}
\begin{cases}
x=r\sin\theta\cos\phi \\
y=r\sin\theta\sin\phi \\
z=r\cos\theta
\end{cases}
\qquad\left(0\leq r\leq a,\,0\leq\theta\leq \frac{\pi}{2},\,0\leq\phi\leq 2\pi\right)
\end{align}
このとき、新たな積分領域\(D’\)は図4のようになる。
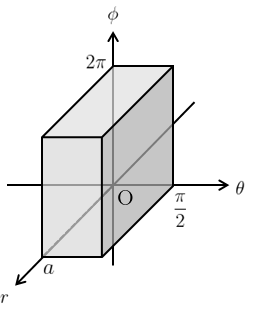
また、ヤコビアンは
\begin{align}
\frac{\partial (x,y,z)}{\partial (r,\theta,\phi)}=r^{2}\sin\theta
\end{align}
となるため、求める定積分は
\begin{align}
&\iint_{D}dxdydz\,2z^{3}(2x^{2}-y^{2}) \notag \\
=&\iint_{D’}\left|\frac{\partial (x,y,z)}{\partial (r,\theta,\phi)}\right|drd\theta d\phi\,2r^{3}\cos^{3}\theta(2r^{2}\sin^{2}\theta\cos^{2}\phi-r^{2}\sin^{2}\theta\sin^{2}\phi) \notag \\
=&2\int_{0}^{a}dr\int_{0}^{\pi/2}d\theta\int_{0}^{2\pi}d\phi\,r^{7}\sin^{3}\theta\cos^{3}\theta(2\cos^{2}\phi-\sin^{2}\phi) \notag \\
=&2\left(\int_{0}^{a}dr\,r^{7}\right)\left(\int_{0}^{\pi/2}d\theta\,\sin^{3}\theta\cos^{3}\theta\right)\left\{\int_{0}^{2\pi}d\phi\,(2\cos^{2}\phi-\sin^{2}\phi)\right\} \notag \\
=&2\left(\int_{0}^{a}dr\,r^{7}\right)\left\{\int_{0}^{\pi/2}d\theta\,\sin^{3}\theta(1-\sin^{2}\theta)\cos\theta\right\}\left\{\int_{0}^{2\pi}d\phi\,(3\cos^{2}\phi-1)\right\} \notag \\
=&2\left(\int_{0}^{a}dr\,r^{7}\right)\left\{\int_{0}^{\pi/2}d\theta\,\cos\theta(\sin^{3}\theta-\sin^{5}\theta)\right\}\left\{\int_{0}^{2\pi}d\phi\,\left(\frac{3}{2}\cos2\phi+\frac{1}{2}\right)\right\} \notag \\
=&2\left[\frac{r^{8}}{8}\right]_{0}^{a}\left[\frac{\sin^{4}\theta}{4}-\frac{\sin^{6}\theta}{6}\right]_{0}^{\pi/2}\frac{1}{2}\left[\frac{3\sin 2\phi}{2}+\phi\right]_{0}^{2\pi} \notag \\
=&\frac{a^{8}}{8}\left(\frac{1}{4}-\frac{1}{6}\right)2\pi=\boxed{\frac{\pi a^{8}}{48}}
\end{align}
となる。
今回で多重積分のパターンごとの解説は終わりにする。
ここからはおまけになるが、問題演習の記事を2つほど作って多重積分の解説を締めようと思う。
続きはこちら。




コメント