前回
にて多重積分は下記4つのパターン
1. 積分領域が定数のみで決まり、被積分関数が変数分離できる場合
2. 積分領域が定数のみで決まり、被積分関数が変数分離できない場合
3. 積分領域が変数に依存し、変数変換する必要がない場合
4. 積分領域が変数に依存し、変数変換する必要がある場合
に分類されることを述べ、パターン1について例題を交えて解説した。
今回は上記パターンの内、2と3を扱う。
2. 積分領域が定数のみで決まり、被積分関数が変数分離できない場合
まず積分領域は前回同様に定数のみで決まるが、被積分関数が変数分離できない場合を扱う。
とは言っても特に小難しい手順があるわけではない。
単純に、ある変数で積分する際は他の変数を固定して(定数とみなして)積分し、次の変数で積分する際も同様に他の変数を固定して積分・・・を繰り返していくだけである。
積分変数を逐次変えて積分を進めていくことから、このような積分を逐次積分と呼ぶ。
例えば被積分関数が二変数関数\(f(x,y)\)なら、先に\(y\)を固定して\(x\)で積分し、次に\(y\)で積分するという手順になる。
\begin{align}
\int_{b_{y}}^{a_{y}}\left\{\int_{b_{x}}^{a_{x}}f(x,y)\,dx\right\}dy
\end{align}
積分変数を選ぶ順番、例えば上記の場合では先に\(x\)で積分するか\(y\)で積分するか、は物理数学の範囲では特に気にしなくて良い。
無論、問題文に指定がある場合はその順序で計算する。
ここでいくつか例題を解いてみよう。
問題
次の定積分を求めよ。
(1) \(\displaystyle{\int_{0}^{\pi/2}dx\int_{0}^{\pi}dy\,\sin(x+y)}\)
(2) \(\displaystyle{\int_{\pi}^{2\pi}dx\int_{0}^{1}dy\,x^{2}y\sin(xy)}\)
解説
(1)
まず\(y\)で積分する。
\begin{align}
\int_{0}^{\pi/2}dx\int_{0}^{\pi}dy\,\sin(x+y)&=\int_{0}^{\pi/2}dx\biggl[-\cos(x+y)\biggr]_{0}^{\pi} \notag \\
&=\int_{0}^{\pi/2}dx\left\{-\cos(x+\pi)+\cos x\right\} \notag \\
&=\int_{0}^{\pi/2}dx\,2\cos x \notag
\end{align}
となる。続いて\(x\)で積分する。
\begin{align}
\int_{0}^{\pi/2}dx\,2\cos x=2\biggl[\sin x\biggr]_{0}^{\pi/2}=\boxed{2}
\end{align}
(2)
まず\(y\)で積分する。\(f(y)=xy,g(y)=-\cos(xy)\)として部分積分法を用いて
\begin{align}
\int_{\pi}^{2\pi}dx\int_{0}^{1}dy\,x^{2}y\sin(xy)&=\int_{\pi}^{2\pi}dx\left\{\biggl[-xy\cos(xy)\biggr]_{0}^{1}-\int_{0}^{1}\left\{-x\cos(xy)\right\}dx\right\} \notag \\
&=\int_{\pi}^{2\pi}dx(\sin x-x\cos x) \notag \\
&=\int_{\pi}^{2\pi}dx\,\sin x-\int_{\pi}^{2\pi}dx\,x\cos x \notag
\end{align}
となる。続いて\(x\)で積分する。こちらも\(f(x)=x,g(x)=\sin x\)として部分積分法を用いて
\begin{align}
\int_{\pi}^{2\pi}dx\,\sin x-\int_{\pi}^{2\pi}dx\,x\cos x&=\int_{\pi}^{2\pi}dx\,\sin x-\left\{\biggl[x\sin x\biggr]_{\pi}^{2\pi}-\int_{\pi}^{2\pi}dx\,\sin x\right\} \notag \\
&=2\int_{\pi}^{2\pi}dx\,\sin x \notag \\
&=2\biggl[-\cos x\biggr]_{\pi}^{2\pi}=\boxed{-4}
\end{align}
となる。
3. 積分領域が変数に依存し、変数変換する必要がない場合
今までは積分領域が定数のみで決まっていたが、ここから積分領域が変数に依存する場合を見ていく。
まずはその中でも、与えられた座標系でそのまま積分できる(変数変換する必要がない)場合から扱う。
このパターンの最大の特徴は積分する順番が決まっていることであり、最初に積分領域が変数に依存する積分から実行する。
例えば二変数関数\(f(x,y)\)を
\begin{align}
\int_{b}^{a}dx\int_{h(x)}^{g(x)}dy\,f(x,y)
\end{align}
のように積分する場合、\(y\)での積分の積分範囲が\(x\)に依存しているため、先に\(y\)で積分してから\(x\)で積分するという順番をとる。
この順番になるのは、\(y\)での積分結果が\(x\)の関数になるためであり、これを先に実行しないと\(x\)での積分の被積分関数が決定しないのである。
そのため被積分関数が変数分離できる場合でも、同時並行で各変数での積分を実行することはできない。
積分領域が変数に依存する積分から実行して、他の変数の積分の被積分関数を決定させる必要がある。
文面だけでは理解しにくいと思うので、ここで例題を解いてみよう。
問題
次の定積分の積分領域を図示した上で、その値を求めよ。
(1) \(\displaystyle{\int_{0}^{1}dx\int_{0}^{-x^{2}+1}dy\,xe^{-y}}\)
(2) \(\displaystyle{\int_{0}^{1}dx\int_{x^{2}}^{x}dy\,(x+y)^{2}}\)
解説
(1)
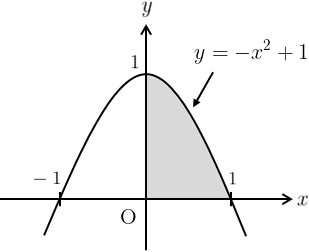
積分領域は右図のようになる。
被積分関数が変数分離できる形だが、\(y\)での積分が\(x\)に依存しているため、まず\(y\)での積分から実行して
\begin{align}
&\int_{0}^{1}dx\int_{0}^{-x^{2}+1}dy\,xe^{-y} \notag \\
=&\int_{0}^{1}dx\,x\biggl[-e^{-y}\biggr]_{0}^{-x^{2}+1} \notag \\
=&\int_{0}^{1}dx\,x(-e^{x^{2}-1}+1) \notag
\end{align}
となる。続いて\(x\)で積分する。
\begin{align}
\int_{0}^{1}dx\,x(-e^{x^{2}-1}+1)&=\int_{0}^{1}dx\,x-\int_{0}^{1}dx\,xe^{x^{2}-1} \notag \\
&=\left[\frac{1}{2}x^{2}\right]_{0}^{1}-\left[\frac{1}{2}e^{x^{2}-1}\right]_{0}^{1} \notag \\
&=\frac{1}{2}-\left(\frac{1}{2}-\frac{1}{2e}\right)=\boxed{\frac{1}{2e}}
\end{align}
(2)
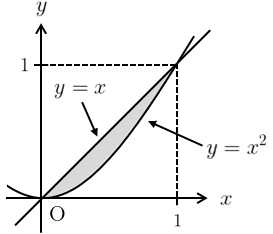
積分領域は右図のようになる。
まず\(y\)での積分が\(x\)に依存しているため、\(y\)での積分から実行して
\begin{align}
&\int_{0}^{1}dx\int_{x^{2}}^{x}dy\,(x+y)^{2}\notag \\
=&\int_{0}^{1}dx\biggl[\frac{(x+y)^{3}}{3}\biggr]_{x^{2}}^{x} \notag \\
=&\frac{1}{3}\int_{0}^{1}dx\left\{8x^{3}-(x+x^{2})^{3}\right\} \notag \\
=&\frac{1}{3}\int_{0}^{1}dx(-x^{6}-3x^{5}-3x^{4}+7x^{3}) \notag \\
\end{align}
となる。続いて\(x\)で積分する。
\begin{align}
\frac{1}{3}\int_{0}^{1}dx(-x^{6}-x^{5}-x^{4}+7x^{3})&=\frac{1}{3}\left[-\frac{1}{7}x^{7}-\frac{1}{2}x^{6}-\frac{3}{5}x^{5}+\frac{7}{4}x^{4}\right]_{0}^{1} \notag \\
&=\frac{1}{3}\left(-\frac{1}{7}-\frac{1}{2}-\frac{3}{5}+\frac{7}{4}\right)=\boxed{\frac{71}{420}}
\end{align}
次回は、パターン3と同じく積分領域が変数に依存し、変数変換する必要がある場合を見ていく。
ここで、以前扱ったヤコビアンを実践的に利用して計算を進めていく。
続きはこちら。




コメント