前回
までで、多重積分をパターン別に紹介し、各パターンに応じた例題を解いてきた。
今回からは、多重積分を逐次積分と変数変換が必要な多重積分の2つに大きくわけた上で問題演習を進めていく。
必ずしもすべてを解く必要はなく、気になる問題があれば参照してもらえればよい。
まずは逐次積分の問題演習からスタート。
被積分関数が変数分離できる場合
問題
積分領域を図示した上で、次の定積分を求めよ。
(1) \(\displaystyle{\int_{-a}^{a}dx\int_{-\sqrt{a^{2}-x^{2}}}^{\sqrt{a^{2}-x^{2}}}dy\quad(a>0)}\)
(2) \(\displaystyle{\int_{0}^{1}dy\int_{0}^{y^{2}}dx\,x\log(1+y)}\)
解説
(1)
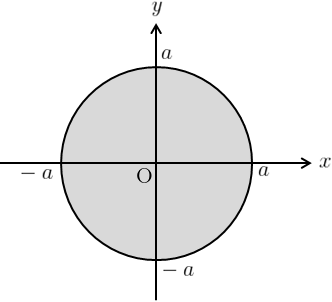
積分領域は右図のようになる。
まず\(y\)での積分が\(x\)に依存しているため、\(y\)での積分から実行して
\begin{align}
\int_{-a}^{a}dx\int_{-\sqrt{a^{2}-x^{2}}}^{\sqrt{a^{2}-x^{2}}}dy&=\int_{-a}^{a}dx\biggl[y\biggr]_{-\sqrt{a^{2}-x^{2}}}^{\sqrt{a^{2}-x^{2}}} \notag \\
&=2\int_{-a}^{a}dx\sqrt{a^{2}-x^{2}}
\end{align}
となる。
続いて\(x\)で積分する。\(x=a\cos\theta\)として置換積分すると、\(\displaystyle{\frac{dx}{d\theta}=-a\sin\theta,\,0\leq\theta\leq\pi}\)より
\begin{align}
2\int_{-a}^{a}dx\sqrt{a^{2}-x^{2}}&=2\int_{\pi}^{0}-a\sin\theta d\theta\sqrt{a^{2}-a^{2}\cos^{2}\theta} \notag \\
&=2a^{2}\int_{0}^{\pi}d\theta\sin^{2}\theta \notag \\
&=2a^{2}\int_{0}^{\pi}d\theta\frac{1}{2}\left(1-\cos2\theta\right) \notag \\
&=a^{2}\left[\theta-\frac{1}{2}\sin2\theta\right]_{0}^{\pi}=\boxed{\pi a^{2}}
\end{align}
となる。
(2)
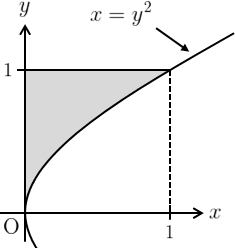
積分領域は右図のようになる。
まず\(x\)での積分が\(y\)に依存しているため、\(x\)での積分から実行して
\begin{align}
\int_{0}^{1}dy\int_{0}^{y^{2}}dx\,x\log(1+y)&=\int_{0}^{1}dy\log(1+y)\left[\frac{1}{2}x^{2}\right]_{0}^{y^{2}} \notag \\
&=\frac{1}{2}\int_{0}^{1}dy\,y^{4}\log(1+y)
\end{align}
となる。
続いて\(y\)で積分する。まず\(f(y)=\log(1+y),\,g(y)=y^{5}/5\)として部分積分法を用いて
\begin{align}
\frac{1}{2}\int_{0}^{1}dy\,y^{4}\log(1+y)&=\frac{1}{2}\left\{\left[\frac{1}{5}y^{5}\log(1+y)\right]_{0}^{1}-\frac{1}{5}\int_{0}^{1}dy\frac{y^{5}}{1+y}\right\}
\end{align}
となる。ここで
\begin{align}
\int_{0}^{1}dy\frac{y^{5}}{1+y}&=\int_{0}^{1}dy\frac{(1+y)^{5}-(5y^{4}+10y^{3}+10y^{2}+5y+1)}{1+y} \notag \\
&=\int_{0}^{1}dy\left\{(1+y)^{4}-\frac{5y(1+y^{3})+10y^{2}(1+y)+1}{1+y}\right\} \notag \\
&=\int_{0}^{1}dy\left\{(1+y)^{4}-5y(1-y+y^{2})-10y^{2}-\frac{1}{1+y}\right\} \notag \\
&=\int_{0}^{1}dy\left\{(1+y)^{4}-5y^{3}-5y^{2}-5y-\frac{1}{1+y}\right\} \notag \\
&=\left[\frac{(1+y)^{5}}{5}-\frac{5}{4}y^{4}-\frac{5}{3}y^{3}-\frac{5}{2}y^{2}-\log(1+y)\right]_{0}^{1} \notag \\
&=\left(\frac{32}{5}-\frac{5}{4}-\frac{5}{3}-\frac{5}{2}-\log2\right)-\frac{1}{5}=\frac{47}{60}-\log2
\end{align}
となるため、これを利用して
\begin{align}
\frac{1}{2}\int_{0}^{1}dy\,y^{4}\log(1+y)&=\frac{1}{2}\left\{\left[\frac{1}{5}y^{5}\log(1+y)\right]_{0}^{1}-\frac{1}{5}\left(\frac{47}{60}-\log2\right)\right\} \notag \\
&=\frac{1}{2}\left(\frac{\log2}{5}-\frac{47}{300}+\frac{\log2}{5}\right)=\boxed{\frac{\log2}{5}-\frac{47}{600}}
\end{align}
となる。
被積分関数が変数分離できない場合
問題
積分領域を図示した上で、次の定積分を求めよ。
(1) \(\displaystyle{\int_{e}^{e^{2}}dy\int_{1}^{e}dx\,\frac{1}{x}\left\{\log(xy)\right\}^{2}}\)
(2) \(\displaystyle{\int_{1/\sqrt{3}}^{1}dx\int_{x^{2}}^{x}dy\,\frac{x}{x^{2}+y^{2}}}\)
解説
(1)

積分領域は右図のようになる。
まず\(x\)で積分する。
\begin{align}
\int_{e}^{e^{2}}dy\int_{1}^{e}dx\,\frac{1}{x}\left\{\log(xy)\right\}^{2}&=\int_{e}^{e^{2}}dy\left[\frac{1}{3}\left\{\log(xy)\right\}^{3}\right]_{1}^{e} \notag \\
&=\frac{1}{3}\int_{e}^{e^{2}}dy\left[\left\{\log (ey)\right\}^{3}-(\log y)^{3}\right] \notag \\
&=\frac{1}{3}\int_{e}^{e^{2}}dy\left[\left\{1+\log y\right\}^{3}-(\log y)^{3}\right] \notag \\
&=\int_{e}^{e^{2}}dy\left\{\frac{1}{3}+\log y+(\log y)^{2}\right\} \notag \\
\end{align}
となる。
続いて\(y\)で積分する。
\begin{align}
\int_{e}^{e^{2}}dy\left\{\frac{1}{3}+\log y+(\log y)^{2}\right\}&=\frac{1}{3}\int_{e}^{e^{2}}dy+\int_{e}^{e^{2}}dy\,\log y+\int_{e}^{e^{2}}dy\,(\log y)^{2}
\end{align}
ここで\(\displaystyle{I_{1}=\int_{e}^{e^{2}}dy\,\log y,\,I_{2}=\int_{e}^{e^{2}}dy\,(\log y)^{2}}\)として別々で計算する。まず\(I_{1}\)については、\(f(y)=\log y,\,g(y)=y\)として部分積分法を用いて
\begin{align}
I_{1}&=\int_{e}^{e^{2}}dy\,\log y \notag \\
&=\biggl[y\log y\biggr]_{e}^{e^{2}}-\int_{e}^{e^{2}}dy \notag \\
&=e^{2}\log e^{2}-e\log e-(e^{2}-e) \notag \\
&=2e^{2}-e-e^{2}+e=e^{2}
\end{align}
となる。続いて\(I_{2}\)については、\(f(y)=(\log y)^{2},\,g(y)=y\)として部分積分法を用いて
\begin{align}
I_{2}&=\int_{e}^{e^{2}}dy\,(\log y)^{2} \notag \\
&=\biggl[y(\log y)^{2}\biggr]_{e}^{e^{2}}-\int_{e}^{e^{2}}dy\,y\cdot\frac{2\log y}{y} \notag \\
&=e^{2}(\log e^{2})^{2}-e(\log e)^{2}-2\int_{e}^{e^{2}}dy\,\log y \notag \\
&=4e^{2}-e-2e^{2}=2e^{2}-e
\end{align}
となる。よって求めた\(I_{1},I_{2}\)を利用して
\begin{align}
\int_{e}^{e^{2}}dy\left\{\frac{1}{3}+\log y+(\log y)^{2}\right\}&=\frac{1}{3}\int_{e}^{e^{2}}dy+I_{1}+I_{2} \notag \\
&=\frac{e^{2}-e}{3}+e^{2}+2e^{2}-e \notag \\
&=\frac{e^{2}-e+9e^{2}-3e}{3}\notag \\
&=\boxed{\frac{10}{3}e^{2}-\frac{4}{3}e}
\end{align}
となる。
(2)
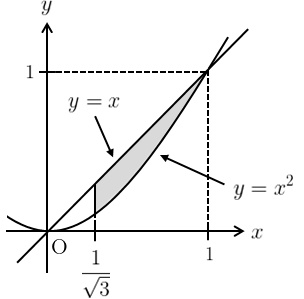
積分領域は右図のようになる。
まず\(y\)での積分が\(x\)に依存しているため、\(y\)での積分から実行して
\begin{align}
\int_{1/\sqrt{3}}^{1}dx\int_{x^{2}}^{x}dy\,\frac{x}{x^{2}+y^{2}}&=\int_{1/\sqrt{3}}^{1}dx\int_{x^{2}}^{x}dy\,\frac{\frac{1}{x}}{1+\left(\frac{y}{x}\right)^{2}} \notag \\
&=\int_{1/\sqrt{3}}^{1}dx\left[\tan^{-1}\frac{y}{x}\right]_{x^{2}}^{x} \notag \\
&=\int_{1/\sqrt{3}}^{1}dx\left(\frac{\pi}{4}-\tan^{-1}x\right)
\end{align}
となる。
続いて\(x\)で積分する。第2項の積分は\(f(x)=\tan^{-1}x,\,g(x)=x\)として部分積分法を用いて
\begin{align}
\int_{1/\sqrt{3}}^{1}dx\left(\frac{\pi}{4}-\tan^{-1}x\right)&=\int_{1/\sqrt{3}}^{1}dx\,\frac{\pi}{4}-\left\{\biggl[x\tan^{-1}x\biggr]_{1/\sqrt{3}}^{1}-\int_{1/\sqrt{3}}^{1}dx\,\frac{x}{1+x^{2}}\right\} \notag \\
&=\frac{\pi}{4}\left(1-\frac{1}{\sqrt{3}}\right)-\left\{\frac{\pi}{4}-\frac{\pi}{6\sqrt{3}}-\biggl[\frac{1}{2}\log(1+x^{2})\biggr]_{1/\sqrt{3}}^{1}\right\} \notag \\
&=\frac{\pi}{6\sqrt{3}}-\frac{\pi}{4\sqrt{3}}+\frac{1}{2}\left(\log2-\log\frac{4}{3}\right) \notag \\
&=-\frac{\pi}{12\sqrt{3}}+\frac{1}{2}(\log2-2\log2+\log3) \notag \\
&=\boxed{\frac{1}{2}\log\frac{3}{2}-\frac{\sqrt{3}}{36}\pi}
\end{align}
となる。
次回も、問題の出し方を少し変えて逐次積分の問題演習を進める。
続きはこちら。




コメント