前回
にて線積分の概要と例題を取り扱った。
今回はその続きで、面積分の概要を眺め、問題の解き方を解説していく。
概要
面積分も線積分と同様にベクトル場に対して実行する積分である。
線積分との違いは「面」と書かれている通り、ある座標系に存在する面に沿って積分を実行することである。
その面では平面でも曲面でも良いし、開いていても閉じていても良い。
例えばベクトル場\(\vec{A}\)があったとき、これを面\(S\)に沿って面積分する場合は
\begin{align}
\iint_{S}\vec{A}\cdot d\vec{S}
\end{align}
を計算する。
ただし\(d\vec{S}\)は面\(S\)を細かく分割した微小領域に法線ベクトル(面に垂直な単位ベクトル)をかけたものであり、面素ベクトルと呼ばれる。
面積分の基本的な計算の手順は下記のようになる。
(1) 面\(S\)上の位置ベクトル\(\vec{r}\)を2つの変数で表す。ここではその変数を\(u,v\)とする。
(2) 位置ベクトル\(\vec{r}\)を\(u,v\)それぞれで偏微分する。
(3) (2)で得た2つの偏微分の外積を取る。ただし外積を取る順番は下記の要領で決定する。
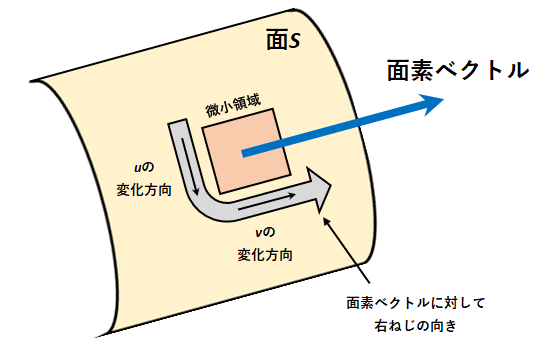
- 面\(S\)上での各変数の正の変化の向きを把握する。例えば図1では、面\(S\)上で\(u\)は下向きに、\(v\)は右向きに変化する。
- 1で把握した各変数の変化の向きを組み合わせたとき、面素ベクトルの向きに対して右ねじの向きになるようにする。例えば図1では、面素ベクトルは画面奥から手前への向きであるため、\(u\to v\)の組み合わせで面素ベクトルに対して右ねじの向きになる。
- 2で把握した組み合わせと同じ順番で、偏微分の外積を取る。例えば\(u\to v\)の順番なら外積は\((\partial \vec{r}/\partial u)\times(\partial \vec{r}/\partial v)\)となる。
(4) (3)で得た外積に各変数の微小量をかける。これが面素ベクトル\(d\vec{S}\)となる。
\begin{align}
d\vec{S}=\left(\frac{\partial \vec{r}}{\partial u}\times \frac{\partial \vec{r}}{\partial v}\right)dudv
\end{align}
(5) (1)での面\(S\)の位置ベクトル\(\vec{r}\)を面積分するベクトル場\(\vec{A}\)に適用する。
(6) (4)で得た面素ベクトル\(d\vec{S}\)と、(5)で変数表示を適用したベクトル場\(\vec{A}\)の内積を計算する。
(7) 面\(S\)上での変数の変化を積分範囲とし、(6)で得た内積を積分する。
面\(S\)が複雑な場合は、面を変数表示できるまで単純な面に分割し、各面について上記の計算を実施して、最後にそれらを足し上げればよい。
これだけではまだイメージがつかないだろうから、実際に例題を解いていこう。
例題1:平面上での面積分
例題1
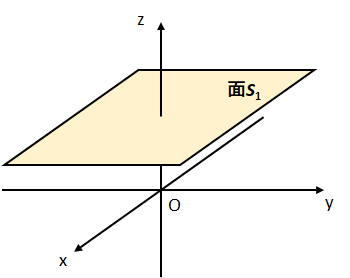
ベクトル場\(\vec{A}_{1}=(0,0,5)\)の平面\(S_{1}:-1\leq x\leq 1,-1\leq y\leq 1,z=2\)上での面積分を求めよ。
ただし、面素ベクトルの向きはz軸正の向きとする。
解説
まず面\(S_{1}\)上の位置ベクトル\(\vec{r}_{1}\)を2つの変数で表す。
面\(S_{1}\)はx-y平面に平行かつ\(z=2\)に位置する平面であるため、位置ベクトルは
\begin{align}
\vec{r}_{1}=(x,y,2) \tag{1}\label{mensekirei1-1-1}
\end{align}
と書ける。
ここでこの位置ベクトル\(\vec{r}_{1}\)を\(x\)および\(y\)で偏微分すると(\ref{mensekirei1-1-1})より
\begin{align}
&\frac{\partial \vec{r}_{1}}{\partial x}=(1,0,0) \tag{2}\label{mensekirei1-1-2}\\
&\frac{\partial \vec{r}_{1}}{\partial y}=(0,1,0) \tag{3}\label{mensekirei1-1-3}
\end{align}
となる。

次にこれら2つの偏微分の外積を取る。
図2のように面素ベクトルの向きがz軸正の向きであるとき、\(x \to y\)の組み合わせで面素ベクトルに対して右ねじの向きになる。
よって外積かける順番は(\(x\)の偏微分)\(\times\)(\(y\)の偏微分)となるため、(\ref{mensekirei1-1-2})と(\ref{mensekirei1-1-3})より
\begin{align}
\frac{\partial \vec{r}_{1}}{\partial x}\times\frac{\partial \vec{r}_{1}}{\partial y}&=(1,0,0)\times(0,1,0)=(0,0,1) \tag{4}\label{mensekirei1-1-4}
\end{align}
と計算できる。
よって面素ベクトルは\(d\vec{S}_{1}\)とすると(\ref{mensekirei1-1-4})の結果を利用して
\begin{align}
d\vec{S}_{1}&=\left(\frac{\partial \vec{r}_{1}}{\partial x}\times\frac{\partial \vec{r}_{1}}{\partial y}\right)dx dy=(0,0,1)dxdy \tag{5}\label{mensekirei1-1-5}
\end{align}
となる。
今回扱うベクトル場\(\vec{A}_{1}\)は一様なベクトル場(変数が含まれていない)ため、そのまま面積分に適用する。
よって面の範囲を考慮すると積分範囲は\(x:-1\to 1,y:-1\to 1\)となるため、面\(S_{1}\)上での面積分は(\ref{mensekirei1-1-5})より
\begin{align}
\iint_{S_{1}}\vec{A}_{1}\cdot d\vec{S}_{1}&=\iint_{S_{1}}(0,0,5)\cdot (0,0,1)dxdy \notag \\
&=5\left(\int_{-1}^{1}dx\right)\left(\int_{-1}^{1}dy\right) \notag \\
&=5\cdot2\cdot 2=\boxed{20} \tag{6}
\end{align}
となる。
例題2:球面上での面積分
例題2
ベクトル場\(\vec{A}_{2}=(2x,2y,2z)\)の球面\(S_{2}:x^{2}+y^{2}+z^{2}=4\)上での面積分を求めよ。
ただし、面素ベクトルの向きは球面に対して外向きとする。
解説
まず面\(S_{2}\)上の位置ベクトル\(\vec{r}_{2}\)を2つの変数で表す。
面\(S_{2}\)は原点Oを中心とする半径2の球面であるため、位置ベクトルは極座標表示を利用して
\begin{align}
\vec{r}_{2}=(2\sin\theta\cos\phi,2\sin\theta\sin\phi,2\cos\theta)\,\quad\left(0\leq\theta\leq\pi,0\leq\phi\leq 2\pi\right) \tag{7}\label{mensekirei1-2-1}
\end{align}
と書ける。
ここでこの位置ベクトル\(\vec{r}_{2}\)を\(\theta\)および\(\phi\)で偏微分すると(\ref{mensekirei1-2-1})より
\begin{align}
&\frac{\partial \vec{r}_{2}}{\partial \theta}=(2\cos\theta\cos\phi,2\cos\theta\sin\phi,-2\sin\theta) \tag{8}\label{mensekirei1-2-2}\\
&\frac{\partial \vec{r}_{2}}{\partial \phi}=(-2\sin\theta\sin\phi,2\sin\theta\cos\phi,0) \tag{9}\label{mensekirei1-2-3}
\end{align}
となる。
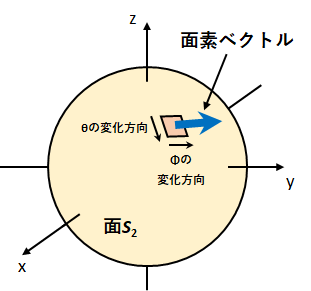
次にこれら2つの偏微分の外積を取る。
図3のように面素ベクトルの向きが球面に対して外向きであるとき、\(\theta\to\phi\)の組み合わせで面素ベクトルに対して右ねじの向きになる。
よって外積かける順番は(\(\theta\)の偏微分)\(\times\)(\(\phi\)の偏微分)となるため、(\ref{mensekirei1-2-2})と(\ref{mensekirei1-2-3})より
\begin{align}
\frac{\partial \vec{r}_{2}}{\partial \theta}\times\frac{\partial \vec{r}_{2}}{\partial \phi}&=(2\cos\theta\cos\phi,2\cos\theta\sin\phi,-2\sin\theta)\times(-2\sin\theta\sin\phi,2\sin\theta\cos\phi,0)\notag \\
&=(4\sin^{2}\theta\cos\phi,4\sin^{2}\theta\sin\phi,4\sin\theta\cos\theta\cos^{2}\phi+4\sin\theta\cos\theta\sin^{2}\phi) \notag \\
&=(4\sin^{2}\theta\cos\phi,4\sin^{2}\theta\sin\phi,4\sin\theta\cos\theta) \notag \\
&=(\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta)4\sin\theta \tag{10}\label{mensekirei1-2-4}
\end{align}
と計算できる。
よって面素ベクトルは\(d\vec{S}_{2}\)とすると(\ref{mensekirei1-2-4})の結果を利用して
\begin{align}
d\vec{S}_{2}&=\left(\frac{\partial \vec{r}_{2}}{\partial \theta}\times\frac{\partial \vec{r}_{2}}{\partial \phi}\right)d\theta d\phi=(\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta)4\sin\theta d\theta d\phi \tag{11}\label{mensekirei1-2-5}
\end{align}
となる。
続いてベクトル場\(\vec{A}_{2}\)に位置ベクトル\(\vec{r}_{2}\)を適用すると
\begin{align}
\vec{A}_{2}&=(2\cdot 2\sin\theta\cos\phi,2\cdot 2\sin\theta\sin\phi,2\cdot 2\cos\theta)\notag \\
&=(4\sin\theta\cos\phi,4\sin\theta\sin\phi,4\cos\theta) \tag{12}\label{mensekirei1-2-6}
\end{align}
となる。
よって面の範囲を考慮すると積分範囲は\(\theta:0\to\pi,\phi:0\to 2\pi\)となるため、面\(S_{2}\)上での面積分は(\ref{mensekirei1-2-5})と(\ref{mensekirei1-2-6})より
\begin{align}
&\iint_{S_{2}}\vec{A}_{2}\cdot d\vec{S}_{2}\notag \\
=&\iint_{S_{2}}(4\sin\theta\cos\phi,4\sin\theta\sin\phi,4\cos\theta)\cdot (\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta)4\sin\theta d\theta d\phi \notag \\
=&16\int_{0}^{\pi}d\theta\int_{0}^{2\pi}d\phi\,(\sin^{2}\theta\cos^{2}\phi+\sin^{2}\theta\sin^{2}\phi+\cos^{2}\theta)\sin\theta \notag \\
=&16\left(\int_{0}^{\pi}\sin\theta\,d\theta\right)\left(\int_{0}^{2\pi}d\phi\right) \notag \\
=&16\biggl[-\cos\theta\biggr]_{0}^{\pi}\cdot 2\pi \notag \\
=&16\cdot 2\cdot 2\pi=\boxed{64\pi} \tag{13}
\end{align}
となる。
例題3:円筒面上での面積分
例題3
ベクトル場\(\vec{A}_{3}=(10x,10y,0)\)の円筒面\(S_{3}:x^{2}+y^{2}=1,-2\leq z\leq 2\)上での面積分を求めよ。
ただし、面素ベクトルの向きは円筒面に対して外向きとする。
解説
まず面\(S_{3}\)上の位置ベクトル\(\vec{r}_{3}\)を2つの変数で表す。
面\(S_{3}\)はz軸を中心とする半径1の円筒面であるため、位置ベクトルは円筒座標表示を利用して
\begin{align}
\vec{r}_{3}=(\cos\theta,\sin\theta,z)\,\quad (0\leq\theta\leq 2\pi,-2\leq z\leq 2) \tag{14}\label{mensekirei1-3-1}
\end{align}
と書ける。
ここでこの位置ベクトル\(\vec{r}_{3}\)を\(\theta\)および\(z\)で偏微分すると(\ref{mensekirei1-3-1})より
\begin{align}
&\frac{\partial \vec{r}_{3}}{\partial \theta}=(-\sin\theta,\cos\theta,0) \tag{15}\label{mensekirei1-3-2}\\
&\frac{\partial \vec{r}_{3}}{\partial z}=(0,0,1) \tag{16}\label{mensekirei1-3-3}
\end{align}
となる。
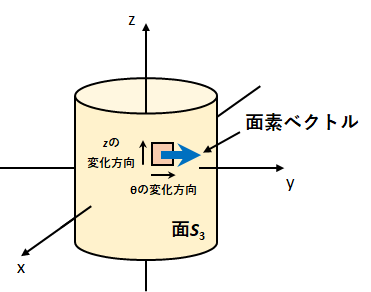
次にこれら2つの偏微分の外積を取る。
図4のように面素ベクトルの向きが円筒面に対して外向きであるとき、\(\theta\to z\)の組み合わせで面素ベクトルに対して右ねじの向きになる。
よって外積かける順番は(\(\theta\)の偏微分)\(\times\)(\(z\)の偏微分)となるため、(\ref{mensekirei1-3-2})と(\ref{mensekirei1-3-3})より
\begin{align}
\frac{\partial \vec{r}_{3}}{\partial \theta}\times\frac{\partial \vec{r}_{3}}{\partial z}=(-\sin\theta,\cos\theta,0)\times(0,0,1)=(\cos\theta,\sin\theta,0) \tag{17}\label{mensekirei1-3-4}
\end{align}
と計算できる。
よって面素ベクトルは\(d\vec{S}_{3}\)とすると(\ref{mensekirei1-3-4})の結果を利用して
\begin{align}
d\vec{S}_{3}&=\left(\frac{\partial \vec{r}_{3}}{\partial \theta}\times\frac{\partial \vec{r}_{3}}{\partial z}\right)d\theta dz=(\cos\theta,\sin\theta,0)d\theta dz \tag{18}\label{mensekirei1-3-5}
\end{align}
となる。
続いてベクトル場\(\vec{A}_{3}\)に位置ベクトル\(\vec{r}_{3}\)を適用すると
\begin{align}
\vec{A}_{3}&=(10\cos\theta,10\sin\theta,0) \tag{19}\label{mensekirei1-3-6}
\end{align}
となる。
よって面の範囲を考慮すると積分範囲は\(\theta:0\to 2\pi,z:-2\to 2\)となるため、面\(S_{3}\)上での面積分は(\ref{mensekirei1-3-5})と(\ref{mensekirei1-3-6})より
\begin{align}
\iint_{S_{3}}\vec{A}_{3}\cdot d\vec{S}_{3}&=\iint_{S_{2}}(10\cos\theta,10\sin\theta,0)\cdot(\cos\theta,\sin\theta,0)d\theta dz \notag \\
&=10\int_{0}^{2\pi}d\theta\int_{-2}^{2}dz\,(\cos^{2}\theta+\sin^{2}\theta) \notag \\
&=10\cdot 2\pi\cdot 4=\boxed{80\pi} \tag{20}
\end{align}
となる。
終わりに
面積分に関してはここで締める。
今回は平面、球面、円筒面というよく見られるパターンの面を扱ったが、これら3つに関しては面素ベクトルをそのまま暗記してしまってもいいと思う。
しかしただ暗記するだけでなく、導出の仕方も含めて暗記して、特殊な面が出題されても対応できるようにはしておくべきだろう。
次回は、線積分と面積分の関係を表したストークスの定理を扱う予定だ。
END




コメント
とてもわかりやすかったです!
ありがとうございます!
お役に立てたようで良かったです。