大学の数学の講義で真っ先に習うものの定番が、テイラー展開とマクローリン展開だろう。
難しそうな名前に尻込みしそうになるかもしれないが、本質は単純だ。
まずは具体的な計算手法には立ち入らず、テイラー展開とマクローリン展開の本質について話す。
なお、マクローリン展開はテイラー展開の一部であるため、今後はマクローリン展開も含めてテイラー展開と呼ぶことにする。
本質
ずばり言うと、テイラー展開の本質は近似である。
例えば、次のような関数があったとする。
\begin{align}
f(x)=\frac{2}{\sqrt{(x^{2}+1)(x^{2}+4)}}e^{-\left(\frac{4}{x^{2}+1}+\frac{1}{x^{2}+4}\right)} \tag{1}\label{func1}
\end{align}
ぱっと見ではどんな形の関数かはわからないが、とにかく\(x=0\)の付近だけでも関数の形がわかるように近似式で表したいとする。
そんなときに、テイラー展開の出番になる。
ちなみにこの(\ref{func1})を、\(x=0\)の周りで二次の項までテイラー展開すると、
\begin{align}
f(x)= e^{-\frac{17}{4}}\left(\frac{17}{4}x^{2}+1\right) \tag{2}\label{func2}
\end{align}
となる。
あの複雑な(\ref{func1})が(\ref{func2})のように二次関数で近似できるのか?
確かめるにはグラフを描くのが手っ取り早い。
両者のグラフを描くと下図のようになる。
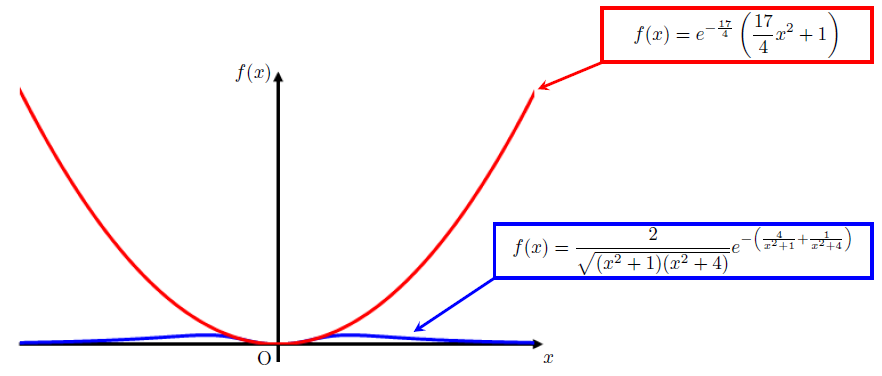

本当に近似できてるのか?
全然形が違うじゃないか。
\(x=0\)付近をよ~く見てほしい。
赤と青のグラフが重なっているのがわかるだろうか。
拡大図を下に示す。
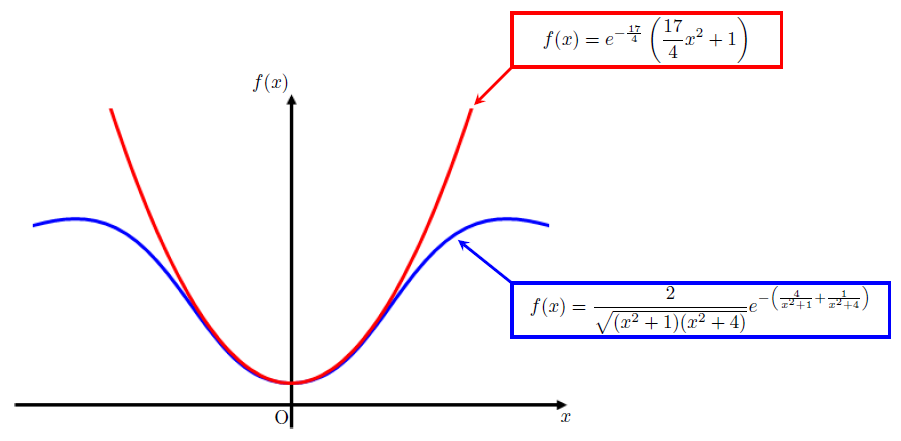
拡大すると、確かに\(x=0\)付近で両者のグラフが重なっているため、\(x=0\)付近では良い近似になっていることがわかる。
このように、関数のある一点の周辺での関数の形を多項式で表現するのがテイラー展開なのだ。
どこで使うのか?
そんな、関数のある一点周辺の形を調べるだけの数学的手法に意味があるのかと思う人もいるかもしれない。
しかし、本当に大した意味がないのなら、大学の講義のごくごく初期にこれが登場することはないはずだ。
実際に物理の研究の現場では、複雑な式をテイラー展開して近似し、議論を簡単にすることはざらにある。
(ぶっちゃけ、近似なしでは物理の研究は成り立たないと考えてよい。)
私自身、研究室時代にはよく使ったし、無論卒業論文にも登場している。
これを知らなきゃ理系失格とまでは言わないが(というかこういう風に相手の背景も理解せずに知っている知らないだけで相手を否定するようなことは私自身嫌いだ)、物理を学ぶ立場にあるならば、必要不可欠な基礎知識として身につけておくべき事項だ。
現時点で知らなかったり、忘れたりしていても心配はいらない。
ここで学び、あるいは復習すれば良いだけだ。
と言うわけで、まずは1変数関数のテイラー展開から見ていくことにする。
下記に続く。





コメント