【微積分】二変数関数の停留点(極大点・極小点・鞍点)

　今回は微分の例題として、二変数関数の停留点を求める問題を扱う。

　停留点とは、ある関数において微分が0、すなわち関数の変化がなくなる点である。

　高校数学における一変数関数の微分の問題で登場する極大点、極小点も停留点の一種だ。

　一変数関数のグラフは多くの場合で曲線であり、微分が0となる場合は極大点か極小点になるしかなかった。

　しかし二変数関数のグラフは多くの場合で曲面であり、極大点と極小点に加えて鞍点と呼ばれる曲面特有の停留点が出現することがある。

　今回は、この鞍点がどういったものかを踏まえつつ、二変数関数の停留点の求め方を示した上で例題を解いていく。

　ただし前提として、今回扱うのは実数値関数に止める。

一般論
例題
終わりに

一般論

　二変数関数\(f(x,y)\)の停留点\((a_{x},a_{y})\)を求めることを考える。

　関数の変化がなくなる点が停留点であるため、停留点では\(x\)方向、\(y\)方向ともにその変化量が0、すなわち

\begin{align}
\frac{\partial f(x,y)}{\partial x}=\frac{\partial f(x,y)}{\partial y}=0 \tag{1}\label{teiryu1}
\end{align}

を満たす点が停留点となる。

　停留点\((a_{x},a_{y})\)を求めたら、次はその種類を判定する。

　これは天下り式になるが、次式で表される行列\(\mathsf{H}\)

\begin{align}
\mathsf{H}=\begin{pmatrix}\displaystyle{\frac{\partial^{2} f(x,y)}{\partial x^{2}}}&\displaystyle{\frac{\partial^{2} f(x,y)}{\partial x\partial y}} \\ \\ \displaystyle{\frac{\partial^{2} f(x,y)}{\partial x\partial y}}&\displaystyle{\frac{\partial^{2} f(x,y)}{\partial y^{2}}}\end{pmatrix} \tag{2}\label{hesian}
\end{align}

に停留点の座標\((a_{x},a_{y})\)を代入した行列

\begin{align}
\mathsf{H}_{(a_{x},a_{y})}=\begin{pmatrix}\displaystyle{\left.\frac{\partial^{2} f(x,y)}{\partial x^{2}}\right|_{x=a_{x},y=a_{y}}}&\displaystyle{\left.\frac{\partial^{2} f(x,y)}{\partial x\partial y}\right|_{x=a_{x},y=a_{y}}} \\ \\ \displaystyle{\left.\frac{\partial^{2} f(x,y)}{\partial x\partial y}\right|_{x=a_{x},y=a_{y}}}&\displaystyle{\left.\frac{\partial^{2} f(x,y)}{\partial y^{2}}\right|_{x=a_{x},y=a_{y}}}\end{pmatrix} \tag{3}\label{hesian2}
\end{align}

の固有値を\(\lambda_{1},\lambda_{2}\)としたとき、

\begin{align}
\begin{cases}
\lambda_{1}>0,\lambda_{2}>0&\to\,\text{極小点}\\
\lambda_{1}<0,\lambda_{2}<0&\to\,\text{極大点}\\
\lambda_{1}\lambda_{2}<0&\to\,\text{鞍点}
\end{cases} \tag{4}\label{teiryuubaai}
\end{align}

となる。

　(\ref{hesian})の行列\(\mathsf{H}\)はヘッセ行列(ヘシアン行列、ヘッシアン)と呼ばれ、実対称行列であるため固有値は必ず実数をとる。

　(\ref{teiryuubaai})のように、2つの固有値\(\lambda_{1},\lambda_{2}\)の積が負になるとき、停留点は鞍点となる。

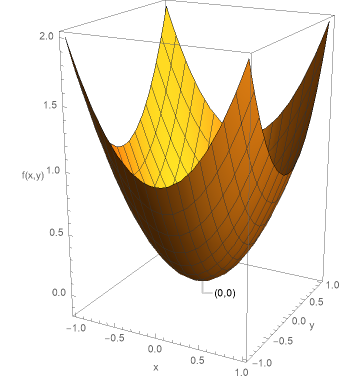
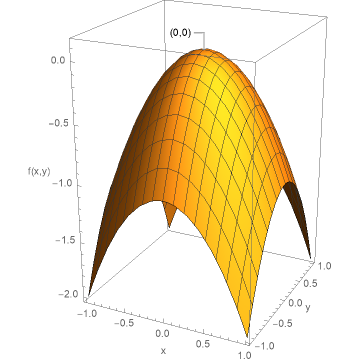
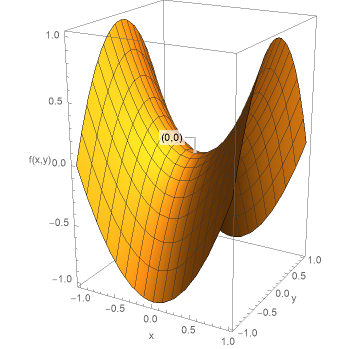
　鞍点とは図3のように、ある方向から見ると極大点だが、その方向と直交する方向から見ると極小点となる点である。

　乗馬するときに馬の背に装着する鞍を連想させる形状をとることから、鞍点と呼ばれる。

例題

　例題として、実際に二変数関数を微分して停留点を求める問題を解いてみよう。

問題

　二変数関数\(f(x,y)=(x^{2}+y^{2})e^{x+y}\)の停留点\((a_{x},a_{y})\)をすべて求め、さらに求めた停留点が極小点、極大点、鞍点のどれにあたるか判定せよ。

解説

　まず、二変数関数\(f(x,y)\)の停留点を求める。

　\(\displaystyle{\frac{\partial f(x,y)}{\partial x}=\frac{\partial f(x,y)}{\partial y}=0}\)を満たす\((x,y)\)の組を求めればよいので、

\begin{gather}
\begin{cases}
\displaystyle{\frac{\partial f(x,y)}{\partial x}=2xe^{x+y}+(x^{2}+y^{2})e^{x+y}=(x^{2}+2x+y^{2})e^{x+y}=0} \\ \\
\displaystyle{\frac{\partial f(x,y)}{\partial y}=2ye^{x+y}+(x^{2}+y^{2})e^{x+y}=(x^{2}+y^{2}+2y)e^{x+y}=0}
\end{cases}\tag{5}\label{teiryuren1}\\
\downarrow\notag\\
\begin{cases}
x^{2}+2x+y^{2}=0 \\
x^{2}+y^{2}+2y=0
\end{cases}\tag{6}\label{teiryuren2}
\end{gather}

となる。

　連立方程式(\ref{teiryuren2})を解くと\((x,y)=(0,0),(-1,-1)\)となるため、停留点は\((a_{x},a_{y})=(0,0),(-1,-1)\)となる。

　続いて停留点の種類を判定する。

　まず、二階の偏導関数を求めると

\begin{align}
&\frac{\partial^{2} f(x,y)}{\partial x^{2}}=(2x+2)e^{x+y}+(x^{2}+2x+y^{2})e^{x+y}=(x^{2}+4x+y^{2}+2)e^{x+y} \tag{7}\label{teiryuxx} \\
&\frac{\partial^{2} f(x,y)}{\partial x\partial y}=2xe^{x+y}+(x^{2}+y^{2}+2y)e^{x+y}=(x^{2}+y^{2}+2x+2y)e^{x+y} \tag{8}\label{teiryuxy} \\
&\frac{\partial^{2} f(x,y)}{\partial y^{2}}=(2y+2)e^{x+y}+(x^{2}+y^{2}+2y)e^{x+y}=(x^{2}+y^{2}+4y+2)e^{x+y} \tag{9}\label{teiryuyy}
\end{align}

となるため、ヘッセ行列は(\ref{hesian})、(\ref{teiryuxx})～(\ref{teiryuyy})より

\begin{align}
\mathsf{H}&=\begin{pmatrix}\displaystyle{\frac{\partial^{2} f(x,y)}{\partial x^{2}}}&\displaystyle{\frac{\partial^{2} f(x,y)}{\partial x\partial y}} \\ \\ \displaystyle{\frac{\partial^{2} f(x,y)}{\partial x\partial y}}&\displaystyle{\frac{\partial^{2} f(x,y)}{\partial y^{2}}}\end{pmatrix} \notag \\
&=e^{x+y}\begin{pmatrix}x^{2}+4x+y^{2}+2&x^{2}+y^{2}+2x+2y\\ \\x^{2}+y^{2}+2x+2y&x^{2}+y^{2}+4y+2\end{pmatrix} \tag{10}\label{hesianrei}
\end{align}

となる。

　後は(\ref{hesianrei})に停留点の座標を代入して、ヘッセ行列の固有値を求めればよい。

　\((a_{x},a_{y})=(0,0)\)のとき、ヘッセ行列は(\ref{hesianrei})より

\begin{align}
\mathsf{H}_{(0,0)}=\begin{pmatrix}2&0\\0&2\end{pmatrix}
\end{align}

となる。

　よって\(\mathsf{H}_{(0,0)}\)の固有値を\(\lambda\)とすると、単位行列を\(\mathsf{I}\)として特性方程式より

\begin{gather}
\text{det}[\mathsf{H}_{(0,0)}-\lambda\mathsf{I}]=0 \notag \\
\begin{vmatrix}2-\lambda & 0\\0&2-\lambda\end{vmatrix}=0\notag\\
(2-\lambda)^{2}=0 \notag \\
\therefore\,\lambda_{1}=2,\lambda_{2}=2
\end{gather}

となる。

　2つの固有値がともに正であるため、停留点\((0,0)\)は極小点である。

　\((a_{x},a_{y})=(-1,-1)\)のとき、ヘッセ行列は(\ref{hesianrei})より

\begin{align}
\mathsf{H}_{(-1,-1)}=e^{-2}\begin{pmatrix}0&-2\\-2&0\end{pmatrix}=\begin{pmatrix}0&-2e^{-2}\\-2e^{-2}&0\end{pmatrix}
\end{align}

となる。

　よって\(\mathsf{H}_{(-1,-1)}\)の固有値を\(\lambda\)とすると、単位行列を\(\mathsf{I}\)として特性方程式より

\begin{gather}
\text{det}[\mathsf{H}_{(-1,-1)}-\lambda\mathsf{I}]=0 \notag \\
\begin{vmatrix}-\lambda & -2e^{-2}\\-2e^{-2}&-\lambda\end{vmatrix}=0\notag\\
\lambda^{2}-(2e^{-2})^{2}=0 \notag \\
\therefore\,\lambda_{1}=2e^{-2},\lambda_{2}=-2e^{-2}
\end{gather}

となる。

　2つの固有値の積が負であるため、停留点\((-1,-1)\)は鞍点である。

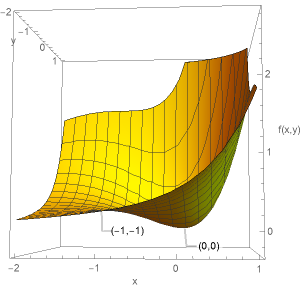
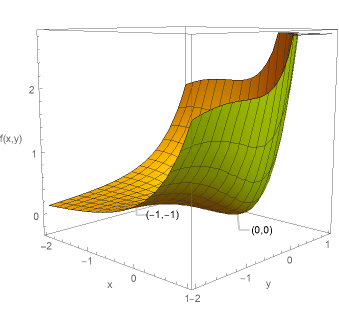
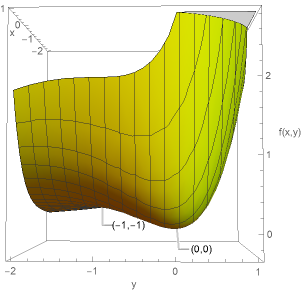
　図4に\(f(x,y)=(x^{2}+y^{2})e^{x+y}\)のグラフを示す。

　実際に\((0,0)\)が極小点、\((-1,-1)\)が鞍点となっていることがわかると思う。