前回
からの続き。
今回は、積分変数を変数変換する多重積分の問題演習を進める。
被積分関数が二変数関数の場合
問題
次の二変数関数\(f(x,y)\)を指定された領域\(D\)で積分せよ。
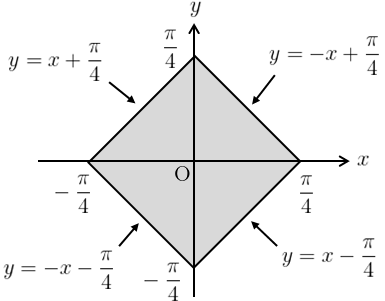
(1) \(\displaystyle{f(x,y)=(x+y)^{2}\cos(x-y),\qquad D:|x|+|y|\leq\frac{\pi}{4}}\)
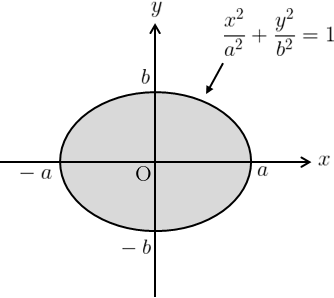
(2) \(\displaystyle{f(x,y)=x^{2}+y^{2}\,\qquad D:\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\leq 1\quad(a,b>0)}\)
解説
(1)
与えられた座標系では、積分領域\(D\)は図1のような正方形になる。そこで今回は変数\((s,t)\)を用いて以下のように座標変換する。
\begin{align}
\begin{cases}
\displaystyle{x=\frac{s+t}{2}} \\ \\
\displaystyle{y=\frac{s-t}{2}}
\end{cases}
\end{align}
このとき\((s,t)\)の範囲は
① \(x\geq0,\,y\geq0\)のとき\(\displaystyle{x+y\leq\pi/4}\) ⇒ \(\displaystyle{s\leq\pi/4}\)
② \(x\leq0,\,y\geq0\)のとき\(\displaystyle{-x+y\leq\pi/4}\) ⇒ \(\displaystyle{t\geq -\pi/4}\)
③ \(x\geq0,\,y\leq0\)のとき\(\displaystyle{x-y\leq\pi/4}\) ⇒ \(\displaystyle{t\leq\pi/4}\)
④ \(x\leq0,\,y\leq0\)のとき\(\displaystyle{-x-y\leq\pi/4}\) ⇒ \(\displaystyle{s\geq-\pi/4}\)
となるため、\((s,t)\)の範囲はそれぞれ\(\displaystyle{-\frac{\pi}{4}\leq s \leq\frac{\pi}{4},\,-\frac{\pi}{4}\leq t\leq\frac{\pi}{4}}\)となり、新たな積分領域\(D’\)は図2のようになる。

また、ヤコビ行列は
\begin{align}
\mathcal{J}(x,y|s,t)=\begin{pmatrix}
\displaystyle{\frac{\partial x}{\partial s}}&\displaystyle{\frac{\partial x}{\partial t}}\\ \\
\displaystyle{\frac{\partial y}{\partial s}}&\displaystyle{\frac{\partial y}{\partial t}}
\end{pmatrix}=
\begin{pmatrix}
\displaystyle{\frac{1}{2}}&\displaystyle{\frac{1}{2}}\\ \\
\displaystyle{\frac{1}{2}}&\displaystyle{-\frac{1}{2}}
\end{pmatrix}
\end{align}
となるため、ヤコビアンは
\begin{align}
\frac{\partial (x,y)}{\partial (s,t)}=\begin{vmatrix}
\displaystyle{\frac{1}{2}}&\displaystyle{\frac{1}{2}}\\ \\
\displaystyle{\frac{1}{2}}&\displaystyle{-\frac{1}{2}}
\end{vmatrix}=-\frac{1}{4}-\frac{1}{4}=-\frac{1}{2}
\end{align}
となる。
よって求める定積分は
\begin{align}
\iint_{D}dxdy\,(x+y)^{2}\cos(x-y)&=\iint_{D’}\left|\frac{\partial (x,y)}{\partial (s,t)}\right|dsdt\,s^{2}\cos t \notag \\
&=\int_{-\pi/4}^{\pi/4}ds\int_{-\pi/4}^{\pi/4}dt\frac{1}{2}s^{2}\cos t \notag \\
&=\frac{1}{2}\int_{-\pi/4}^{\pi/4}ds\,s^{2}\int_{-\pi/4}^{\pi/4}dt\,\cos t \notag \\
&=\frac{1}{2}\left[\frac{1}{3}s^{3}\right]_{-\pi/4}^{\pi/4}\biggl[\sin t\biggr]_{-\pi/4}^{\pi/4} \notag \\
&=\frac{1}{6}\left\{\left(\frac{\pi}{4}\right)^{3}-\left(-\frac{\pi}{4}\right)^{3}\right\}\left\{\frac{1}{\sqrt{2}}-\left(-\frac{1}{\sqrt{2}}\right)\right\} \notag \\
&=\frac{1}{6}\cdot\frac{2\pi^{3}}{64}\cdot\frac{2}{\sqrt{2}}=\boxed{\frac{\sqrt{2}}{192}\pi^{3}}
\end{align}
となる。
(2)
与えられた座標系では、積分領域\(D\)は図3のように楕円になる。そこで今回は変数\((t,\theta)\)を用いて以下のように座標変換する。
\begin{align}
\begin{cases}
x=at\cos\theta \\
y=bt\sin\theta
\end{cases}
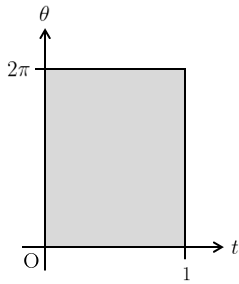
\qquad(0\leq t\leq 1,\,0\leq\theta\leq 2\pi)
\end{align}
このとき、新たな積分領域\(D’\)は図4のようになる。
また、ヤコビ行列は
\begin{align}
\mathcal{J}(x,y|t,\theta)=\begin{pmatrix}
\displaystyle{\frac{\partial x}{\partial t}}&\displaystyle{\frac{\partial x}{\partial \theta}}\\ \\
\displaystyle{\frac{\partial y}{\partial t}}&\displaystyle{\frac{\partial y}{\partial \theta}}
\end{pmatrix}=
\begin{pmatrix}
\displaystyle{a\cos\theta}&\displaystyle{-at\sin\theta}\\ \\
\displaystyle{b\sin\theta}&\displaystyle{bt\cos\theta}
\end{pmatrix}
\end{align}
となるため、ヤコビアンは
\begin{align}
\frac{\partial (x,y)}{\partial (t,\theta)}=\begin{vmatrix}
\displaystyle{a\cos\theta}&\displaystyle{-at\sin\theta}\\ \\
\displaystyle{b\sin\theta}&\displaystyle{bt\cos\theta}
\end{vmatrix}=abt\cos^{2}\theta-(-abt\sin^{2}\theta)=abt
\end{align}
となる。
よって求める定積分は
\begin{align}
\iint_{D}dxdy\,(x^{2}+y^{2})&=\iint_{D’}\left|\frac{\partial (x,y)}{\partial (t,\theta)}\right|dtd\theta\,(a^{2}t^{2}\cos^{2}\theta+b^{2}t^{2}\sin^{2}\theta) \notag \\
&=\int_{0}^{1}dt\int_{0}^{2\pi}d\theta\,abt^{3}(a^{2}\cos^{2}\theta+b^{2}\sin^{2}\theta) \notag \\
&=ab\int_{0}^{1}dt\,t^{3}\int_{0}^{2\pi}d\theta\,(a^{2}\cos^{2}\theta+b^{2}\sin^{2}\theta) \notag \\
&=ab\int_{0}^{1}dt\,t^{3}\int_{0}^{2\pi}d\theta\,\left\{\frac{a^{2}}{2}\left(1+\cos2\theta\right)+\frac{b^{2}}{2}\left(1-\cos2\theta\right)\right\} \notag \\
&=ab\left[\frac{1}{4}t^{4}\right]_{0}^{1}\left[\frac{a^{2}}{2}\left(\theta+\frac{1}{2}\sin2\theta\right)+\frac{b^{2}}{2}\left(\theta-\frac{1}{2}\sin2\theta\right)\right]_{0}^{2\pi} \notag \\
&=\frac{ab}{4}(\pi a^{2}+\pi b^{2})=\boxed{\frac{\pi ab}{4}(a^{2}+b^{2})}
\end{align}
となる。
被積分関数が三変数関数の場合
問題
次の三変数関数\(f(x,y,z)\)を指定された領域\(D\)で積分せよ。
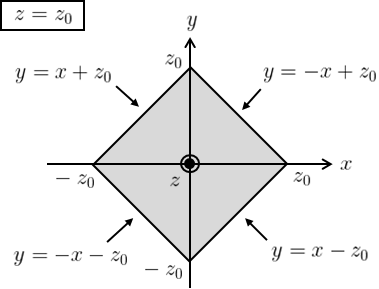
(1) \(\displaystyle{f(x,y)=z(x^{2}-y^{2})^{2}\,\qquad D:|x|+|y|\leq z,\,0\leq z\leq 1}\)
(2) \(\displaystyle{f(x,y)=x^{2}+y^{2}+z^{2}\,\qquad D:\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}\leq 1\quad(a,b,c>0)}\)
解説
(1)
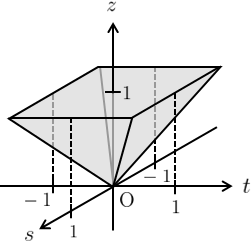
与えられた座標系では、積分領域\(D\)は図5のような正四角錐になる。

そこで今回は変数\((x,y)\)を変数\((s,t)\)を用いて以下のように座標変換する。
\begin{align}
\begin{cases}
\displaystyle{x=\frac{s+t}{2}} \\ \\
\displaystyle{y=\frac{s-t}{2}}
\end{cases}
\end{align}
このとき\((s,t)\)の範囲は
① \(x\geq0,\,y\geq0\)のとき\(\displaystyle{x+y\leq z}\) ⇒ \(\displaystyle{s\leq z}\)
② \(x\leq0,\,y\geq0\)のとき\(\displaystyle{-x+y\leq z}\) ⇒ \(\displaystyle{t\geq -z}\)
③ \(x\geq0,\,y\leq0\)のとき\(\displaystyle{x-y\leq z}\) ⇒ \(\displaystyle{t\leq z}\)
④ \(x\leq0,\,y\leq0\)のとき\(\displaystyle{-x-y\leq z}\) ⇒ \(\displaystyle{s\geq-z}\)
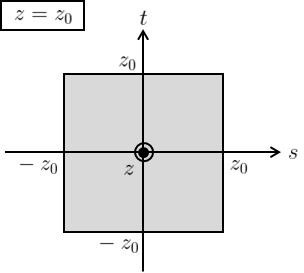
となるため、\((s,t)\)の範囲はそれぞれ\(\displaystyle{-z\leq s \leq z,\,-z\leq t\leq z}\)となり、新たな積分領域\(D’\)は図7のようになる。
また、ヤコビ行列は
\begin{align}
\mathcal{J}(x,y|s,t)=\begin{pmatrix}
\displaystyle{\frac{\partial x}{\partial s}}&\displaystyle{\frac{\partial x}{\partial t}}\\ \\
\displaystyle{\frac{\partial y}{\partial s}}&\displaystyle{\frac{\partial y}{\partial t}}
\end{pmatrix}=
\begin{pmatrix}
\displaystyle{\frac{1}{2}}&\displaystyle{\frac{1}{2}}\\ \\
\displaystyle{\frac{1}{2}}&\displaystyle{-\frac{1}{2}}
\end{pmatrix}
\end{align}
となるため、ヤコビアンは
\begin{align}
\frac{\partial (x,y)}{\partial (s,t)}=\begin{vmatrix}
\displaystyle{\frac{1}{2}}&\displaystyle{\frac{1}{2}}\\ \\
\displaystyle{\frac{1}{2}}&\displaystyle{-\frac{1}{2}}
\end{vmatrix}=-\frac{1}{4}-\frac{1}{4}=-\frac{1}{2}
\end{align}
となる。
よって求める定積分は
\begin{align}
\iiint_{D}dxdydz\,z(x^{2}-y^{2})^{2}&=\iiint_{D’}\left|\frac{\partial (x,y)}{\partial (s,t)}\right|dsdtdz\frac{z\left\{(s+t)^{2}-(s-t)^{2}\right\}^{2}}{16} \notag \\
&=\int_{0}^{1}dz\int_{-z}^{z}ds\int_{-z}^{z}dt\,\frac{1}{2}\cdot\frac{z(2s\cdot 2t)^{2}}{16} \notag \\
&=\frac{1}{2}\int_{0}^{1}dz\int_{-z}^{z}ds\int_{-z}^{z}dt\,zs^{2}t^{2}
\end{align}
となる。
\(s,t\)の積分が\(z\)に依存しているため、\(s,t\)での積分から実行する。
\begin{align}
\frac{1}{2}\int_{0}^{1}dz\int_{-z}^{z}ds\int_{-z}^{z}dt\,zs^{2}t^{2}&=\frac{1}{2}\int_{0}^{1}dz\,z\int_{-z}^{z}ds\,s^{2}\int_{-z}^{z}dt\,t^{2} \notag \\
&=\frac{1}{2}\int_{0}^{1}dz\,z\left[\frac{1}{3}s^{3}\right]_{-z}^{z}\left[\frac{1}{3}t^{3}\right]_{-z}^{z} \notag \\
&=\frac{1}{2}\int_{0}^{1}dz\,z\cdot\frac{1}{3}\left\{z^{3}-(-z)^{3}\right\}\cdot\frac{1}{3}\left\{z^{3}-(-z)^{3}\right\} \notag \\
&=\frac{2}{9}\int_{0}^{1}dz\,z^{7}
\end{align}
となる。
続いて\(z\)で積分する。
\begin{align}
\frac{2}{9}\int_{0}^{1}dz\,z^{7}=\frac{2}{9}\left[\frac{1}{8}z^{8}\right]_{0}^{1}=\frac{2}{9}\cdot\frac{1}{8}=\boxed{\frac{1}{36}}
\end{align}
(2)
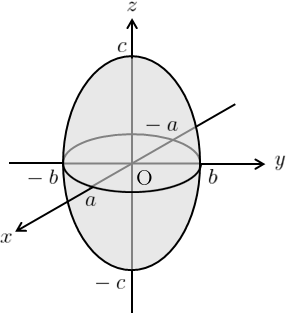
与えられた座標系では、積分領域\(D\)は図9のように楕円体になる。そこで今回は変数\((t,\theta,\phi)\)を用いて以下のように座標変換する。
\begin{align}
\begin{cases}
x=at\sin\theta\cos\phi \\
y=bt\sin\theta\sin\phi \\
z=ct\cos\theta
\end{cases}
\qquad(0\leq t\leq 1,\,0\leq\theta\leq \pi,\,0\leq\phi\leq 2\pi)
\end{align}
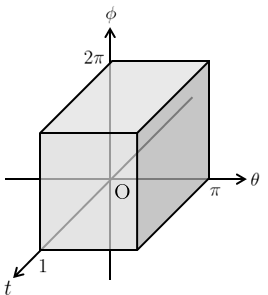
このとき、新たな積分領域\(D’\)は図10のようになる。
また、ヤコビ行列は
\begin{align}
\mathcal{J}(x,y,z|t,\theta,\phi)=\begin{pmatrix}
\displaystyle{\frac{\partial x}{\partial t}}&\displaystyle{\frac{\partial x}{\partial \theta}}&\displaystyle{\frac{\partial x}{\partial \phi}}\\ \\
\displaystyle{\frac{\partial y}{\partial t}}&\displaystyle{\frac{\partial y}{\partial \theta}}&\displaystyle{\frac{\partial y}{\partial \phi}}\\ \\
\displaystyle{\frac{\partial z}{\partial t}}&\displaystyle{\frac{\partial z}{\partial \theta}}&\displaystyle{\frac{\partial z}{\partial \phi}}
\end{pmatrix}=
\begin{pmatrix}
\displaystyle{a\sin\theta\cos\phi}&\displaystyle{at\cos\theta\cos\phi}&\displaystyle{-at\sin\theta\sin\phi}\\ \\
\displaystyle{b\sin\theta\sin\phi}&\displaystyle{bt\cos\theta\sin\phi}&\displaystyle{bt\sin\theta\cos\phi}\\ \\
\displaystyle{c\cos\theta}&\displaystyle{-ct\sin\theta}&0
\end{pmatrix}
\end{align}
となるため、ヤコビアンは
\begin{align}
\frac{\partial (x,y,z)}{\partial (t,\theta,\phi)}&=\begin{vmatrix}
\displaystyle{a\sin\theta\cos\phi}&\displaystyle{at\cos\theta\cos\phi}&\displaystyle{-at\sin\theta\sin\phi}\\ \\
\displaystyle{b\sin\theta\sin\phi}&\displaystyle{bt\cos\theta\sin\phi}&\displaystyle{bt\sin\theta\cos\phi}\\ \\
\displaystyle{c\cos\theta}&\displaystyle{-ct\sin\theta}&0
\end{vmatrix}\notag \\
&=abct^{2}\cos^{2}\theta\sin\theta\cos^{2}\phi+abct^{2}\sin^{3}\theta\sin^{2}\phi \notag \\
&\quad+abct^{2}\cos^{2}\theta\sin\theta\sin^{2}\phi+abct^{2}\sin^{3}\theta\cos^{2}\phi \notag \\
&=abct^{2}\cos^{2}\theta\sin\theta+abct^{2}\sin^{3}\theta \notag \\
&=abct^{2}\sin\theta
\end{align}
となる。
よって求める定積分は
\begin{align}
&\iiint_{D}dxdydz\,(x^{2}+y^{2}+z^{2})\notag \\
=&\iiint_{D’}\left|\frac{\partial (x,y,z)}{\partial (t,\theta,\phi)}\right|dtd\theta d\phi\,(a^{2}t^{2}\sin^{2}\theta\cos^{2}\phi+b^{2}t^{2}\sin^{2}\theta\sin^{2}\phi+c^{2}t^{2}\cos^{2}\theta) \notag \\
=&\int_{0}^{1}dt\int_{0}^{\pi}d\theta\int_{0}^{2\pi}d\phi\,abct^{2}\sin\theta\cdot t^{2}(a^{2}\sin^{2}\theta\cos^{2}\phi+b^{2}\sin^{2}\theta\sin^{2}\phi+c^{2}\cos^{2}\theta) \notag \\
=&abc\int_{0}^{1}dt\,t^{4}\int_{0}^{\pi}d\theta\int_{0}^{2\pi}d\phi\,(a^{2}\sin^{3}\theta\cos^{2}\phi+b^{2}\sin^{3}\theta\sin^{2}\phi+c^{2}\sin\theta\cos^{2}\theta)
\end{align}
となる。
ここで\(\displaystyle{I_{1}=\int_{0}^{\pi}d\theta\int_{0}^{2\pi}d\phi\,a^{2}\sin^{3}\theta\cos^{2}\phi,\,}\)\(\displaystyle{I_{2}=\int_{0}^{\pi}d\theta\int_{0}^{2\pi}d\phi\,b^{2}\sin^{3}\theta\sin^{2}\phi,\,}\)\(\displaystyle{I_{3}=\int_{0}^{\pi}d\theta\int_{0}^{2\pi}d\phi\,c^{2}\sin\theta\cos^{2}\theta}\)として別々で計算する。
まず\(I_{1}\)については、
\begin{align}
I_{1}&=\int_{0}^{\pi}d\theta\int_{0}^{2\pi}d\phi\,a^{2}\sin^{3}\theta\cos^{2}\phi \notag \\
&=a^{2}\int_{0}^{\pi}d\theta\,\sin^{3}\theta\int_{0}^{2\pi}d\phi\,\cos^{2}\phi \notag \\
&=a^{2}\int_{0}^{\pi}d\theta\,\sin\theta(1-\cos^{2}\theta)\int_{0}^{2\pi}d\phi\,\frac{1}{2}(1+\cos 2\phi) \notag \\
&=\frac{a^{2}}{2}\left[-\cos\theta+\frac{1}{3}\cos^{3}\theta\right]_{0}^{\pi}\left[\phi+\frac{1}{2}\sin 2\phi\right]_{0}^{2\pi} \notag \\
&=\frac{a^{2}}{2}\left\{\left(1-\frac{1}{3}\right)-\left(-1+\frac{1}{3}\right)\right\}\cdot 2\pi=\frac{4}{3}\pi a^{2}
\end{align}
となる。次に\(I_{2}\)については、
\begin{align}
I_{2}&=\int_{0}^{\pi}d\theta\int_{0}^{2\pi}d\phi\,b^{2}\sin^{3}\theta\sin^{2}\phi \notag \\
&=b^{2}\int_{0}^{\pi}d\theta\,\sin^{3}\theta\int_{0}^{2\pi}d\phi\,\sin^{2}\phi \notag \\
&=b^{2}\int_{0}^{\pi}d\theta\,\sin\theta(1-\cos^{2}\theta)\int_{0}^{2\pi}d\phi\,\frac{1}{2}(1-\cos 2\phi) \notag \\
&=\frac{b^{2}}{2}\left[-\cos\theta+\frac{1}{3}\cos^{3}\theta\right]_{0}^{\pi}\left[\phi-\frac{1}{2}\sin 2\phi\right]_{0}^{2\pi} \notag \\
&=\frac{b^{2}}{2}\left\{\left(1-\frac{1}{3}\right)-\left(-1+\frac{1}{3}\right)\right\}\cdot 2\pi=\frac{4}{3}\pi b^{2}
\end{align}
となる。最後に\(I_{3}\)については、
\begin{align}
I_{3}&=\int_{0}^{\pi}d\theta\int_{0}^{2\pi}d\phi\,c^{2}\sin\theta\cos^{2}\theta \notag \\
&=c^{2}\int_{0}^{\pi}d\theta\,\sin\theta\cos^{2}\theta\int_{0}^{2\pi}d\phi \notag \\
&=c^{2}\left[-\frac{1}{3}\cos^{3}\theta\right]_{0}^{\pi}\cdot 2\pi \notag \\
&=c^{2}\left(\frac{1}{3}+\frac{1}{3}\right)\cdot 2\pi=\frac{4}{3}\pi c^{2}
\end{align}
となる。
よって求めた\(I_{1},I_{2},I_{3}\)を利用して
\begin{align}
&abc\int_{0}^{1}dt\,t^{4}\int_{0}^{\pi}d\theta\int_{0}^{2\pi}d\phi\,(a^{2}\sin^{3}\theta\cos^{2}\phi+b^{2}\sin^{3}\theta\sin^{2}\phi+c^{2}\sin\theta\cos^{2}\theta) \notag \\
=&abc\int_{0}^{1}dt\,t^{4}(I_{1}+I_{2}+I_{3}) \notag \\
=&abc\left[\frac{1}{5}t^{5}\right]_{0}^{1}\left(\frac{4}{3}\pi a^{2}+\frac{4}{3}\pi b^{2}+\frac{4}{3}\pi c^{2}\right)\notag \\
=&\boxed{\frac{4}{15}\pi abc(a^{2}+b^{2}+c^{2})}
\end{align}
となる。
終わりに
これで、ヤコビ行列の導入から多重積分まで数学記事を一旦締めることにする。
次に数学をやるならベクトル解析だが、これも記事にするには重いので一旦勉強する時間を挟むことになる。
そもそも記事化できるのか不明だが、やれるだけやってみようと思う。
END





コメント