まででビオ・サバールの法則を使う問題を解説してきた。
今回は、アンペールの法則の典型問題を解説していく。
アンペールの法則
\begin{align}
\int_{C}\vec{B}(\vec{r})\cdot d\vec{s}=\mu_{0}I \label{am}\tag{1}
\end{align}
無限長の直線電流が作る磁場
下記記事でビオ・サバールの法則を使って解いた問題を、アンペールの法則で解きなおしてみる。
問題1
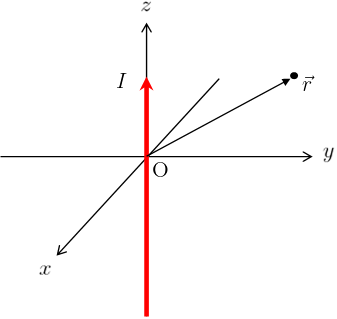
z軸上に太さを無視できる無限長の導線があり、その導線にz軸正の向きに定常電流\(I\)が流れている。
このとき、定常電流\(I\)が位置\(\vec{r}\)に作る磁場\(\vec{B}(\vec{r})\)を求めよ。
解説
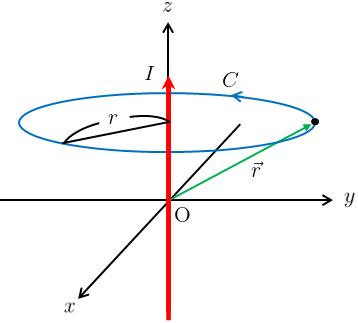
ガウスの法則では閉曲面の法線ベクトルと電場の方向を揃えたように、アンペールの法則では積分経路\(C\)と磁場の方向を揃えると計算が楽になる。
直線電流の場合は磁場の向きは右ねじの向きになる。
そこで経路\(C\)を図2のように、磁場を求めたい位置を含み、x-y平面と平行で中心をz軸が貫く円にとる。
また対称性から、この円上では磁場の大きさは一定になる。
このとき、円筒座標系で考えれば
\begin{align}
&\vec{B}(\vec{r})=|\vec{B}(\vec{r})|(-\sin\theta,\cos\theta,0) \label{linibamp}\tag{2}\\
&d\vec{s}=rd\theta(-\sin\theta,\cos\theta,0) \label{rdtheta2} \tag{3}
\end{align}
となるため、この(\ref{linibamp})と(\ref{rdtheta2})を(\ref{am})の左辺に代入して計算を進めれば
\begin{align}
\int_{C}\vec{B}(\vec{r})\cdot d\vec{s}&=\int_{0}^{2\pi}|\vec{B}(\vec{r})|(-\sin\theta,\cos\theta,0)\cdot rd\theta(-\sin\theta,\cos\theta,0) \\
&=\int_{0}^{2\pi}|\vec{B}(\vec{r})|rd\theta\\
&=2\pi r|\vec{B}(\vec{r})| \label{liniamp2}\tag{4}
\end{align}
となるため、この(\ref{liniamp2})を(\ref{am})に代入すれば
\begin{gather}
2\pi r|\vec{B}(\vec{r})|=\mu_{0}I\\
|\vec{B}(\vec{r})|=\frac{\mu_{0}I}{2\pi r} \label{liniampookisa}\tag{5}
\end{gather}
となる。
以上より、求める磁場は(\ref{linibamp})と(\ref{liniampookisa})より
\begin{gather}
\vec{B}(\vec{r})=|\vec{B}(\vec{r})|(-\sin\theta,\cos\theta,0)=\frac{\mu_{0}I}{2\pi r}(-\sin\theta,\cos\theta,0)\\
\therefore\boxed{\vec{B}(\vec{r})=\frac{\mu_{0}I}{2\pi r}(-\sin\theta,\cos\theta,0)}
\end{gather}
となる。
無限長の円筒電流が作る磁場
先の問題1と同じ考え方で、円筒電流が作る磁場を求めることができる。
問題2
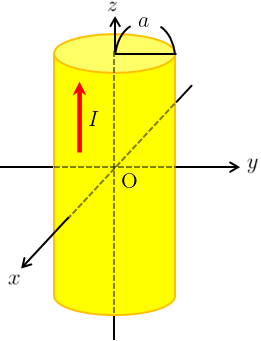
z軸を軸とする半径aの無限に長い円筒内に、z軸正の向きに一様な電流密度で定常電流\(I\)が流れている。このとき、
(a) 円筒内部での磁場\(\vec{B}_{\text{in}}(\vec{r})\)を求めよ。
(b) 円筒外部での磁場\(\vec{B}_{\text{out}}(\vec{r})\)を求めよ。
解説
系としては、問題1の無限長の直線電流が太さをもっただけである。
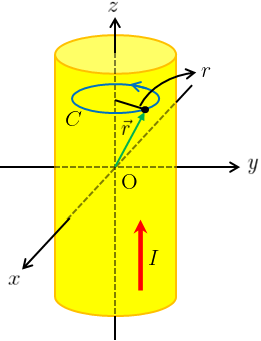
よって経路\(C\)は問題1と同様に磁場を求めたい位置を含み、x-y平面と平行で中心をz軸が貫く円にとればよい。
このとき結局、磁場の向きも(\ref{am})の左辺の求め方も問題1と一緒になり、円筒座標系を導入して
\begin{align}
&\vec{B}(\vec{r})=|\vec{B}(\vec{r})|(-\sin\theta,\cos\theta,0) \label{linibamp2}\tag{6}\\
&\int_{C}\vec{B}(\vec{r})\cdot d\vec{s}=2\pi r|\vec{B}(\vec{r})| \label{entosahen}\tag{7}
\end{align}
となる。
(a) 円筒内の場合
図4のように経路\(C\)は円筒内部に収まっているため、(\ref{am})の右辺の電流はこの経路\(C\)内を貫く電流\(I_{\text{in}}\)のみが対象となる。
すなわち(\ref{am})と(\ref{entosahen})より
\begin{align}
2\pi r|\vec{B}_{\text{in}}(\vec{r})|=\mu_{0}I_{\text{in}} \label{entonaiam}\tag{8}
\end{align}
となる。
円筒内に一様に電流\(I\)が流れているため、電流密度は\(\displaystyle{\frac{I}{\pi a^{2}}}\)となり、経路\(C\)内に流れる電流\(I_{\text{in}}\)は
\begin{align}
I_{\text{in}}=\frac{I}{\pi a^{2}}\cdot \pi r^{2}=\frac{Ir^{2}}{a^{2}} \label{entonaidenryu}\tag{9}
\end{align}
となる。
よって(\ref{entonaidenryu})を(\ref{entonaiam})に代入して整理すれば
\begin{gather}
2\pi r|\vec{B}_{\text{in}}(\vec{r})|=\mu_{0}\cdot\frac{Ir^{2}}{a^{2}}\\
|\vec{B}_{\text{in}}(\vec{r})|=\frac{\mu_{0}Ir}{2\pi a^{2}} \label{entounaijibaoo}\tag{10}
\end{gather}
となる。
以上より、求める磁場は(\ref{linibamp2})と(\ref{entounaijibaoo})より
\begin{align}
\boxed{\vec{B}_{\text{in}}=\frac{\mu_{0}Ir}{2\pi a^{2}}(-\sin\theta,\cos\theta,0)}
\end{align}
となり、磁場の大きさは中心軸からの距離に比例することがわかる。

(b) 円筒外部の場合
図5のように、経路\(C\)内に円筒電流がすべて収まっているため(\ref{am})の右辺の電流は全電流\(I\)をそのまま代入すればよい。
すなわち(\ref{am})と(\ref{entosahen})より
\begin{gather}
2\pi r|\vec{B}_{\text{out}}(\vec{r})|=\mu_{0}I\\
|\vec{B}_{\text{out}}(\vec{r})|=\frac{\mu_{0}I}{2\pi r}
\label{entogaiam}\tag{11}
\end{gather}
となる。
以上より、求める磁場は(\ref{linibamp2})と(\ref{entogaiam})より
\begin{align}
\boxed{\vec{B}_{\text{out}}(\vec{r})=\frac{\mu_{0}I}{2\pi r}(-\sin\theta,\cos\theta,0)}
\end{align}
となり、円筒の外に出ると磁場の大きさは中心軸からの距離に反比例することがわかる。
ソレノイドが作る磁場
前回の記事では、ビオ・サバールの法則で円形電流が中心軸に作る磁場を求め、さらにそれを積分することでソレノイドが中心軸に作る磁場を求めた。
今回はその結果を利用して、ソレノイドが中心軸以外の領域に作る磁場をアンペールの法則から求める。
問題2
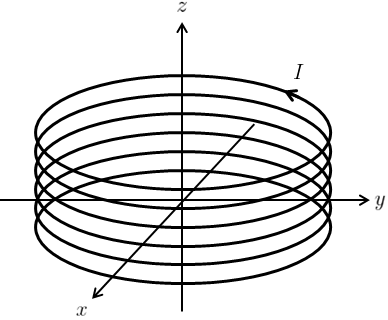
半径\(a\)、単位長さ当たりの巻き数が\(n\)、中心軸がz軸の無限に長いソレノイドがあり、z軸に対して右ねじの向きに定常電流\(I\)が流れている。このとき、
(a) ソレノイド内部での磁場\(\vec{B}_{\text{in}}(\vec{r})\)を求めよ。
(b) ソレノイド外部での磁場\(\vec{B}_{\text{out}}(\vec{r})\)を求めよ。
ただし、ソレノイドが中心軸上(z軸上)に作る磁場\(\vec{B}(\vec{r})=\mu_{0}nI(0,0,1)\)を利用してよい。
解説
対称性を考えると、磁場はz方向にのみ存在し、z方向に一定と考えられる。
そこで、積分経路\(C\)をz-x面に平行な長方形にとることにする。
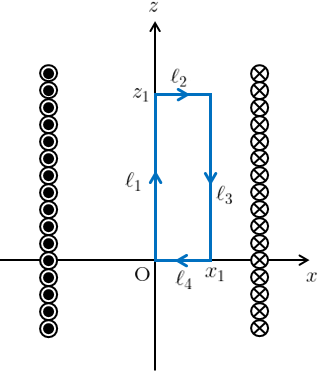
(a) ソレノイド内部の場合
まずソレノイド内部に関しては、図7のように積分経路\(C\)を青色の長方形にとると(\ref{am})の左辺は
\begin{align}
\int_{C}\vec{B}(\vec{r})\cdot d\vec{s}=\int_{\ell_{1}}\vec{B}_{\ell_{1}}(\vec{r})\cdot d\vec{s}_{\ell_{1}}+\int_{\ell_{2}}\vec{B}_{\ell_{2}}(\vec{r})\cdot d\vec{s}_{\ell_{2}}+\int_{\ell_{3}}\vec{B}_{\ell_{3}}(\vec{r})\cdot d\vec{s}_{\ell_{3}}+\int_{\ell_{4}}\vec{B}_{\ell_{4}}(\vec{r})\cdot d\vec{s}_{\ell_{4}}\label{soreamp1}\tag{12}
\end{align}
となる。
ここでx方向の磁場は0なので、(\ref{soreamp1})の第2項と第4項は0になる。
また、
\begin{align}
&\vec{B}_{\ell_{1}}(\vec{r})=\mu_{0}nI(0,0,1)\label{bell1}\tag{13}\\
&d\vec{s}_{\ell_{1}}=dz(0,0,1)\label{dsell1}\tag{14}\\
&d\vec{s}_{\ell_{3}}=dz(0,0,-1)\label{dsell3}\tag{15}
\end{align}
であり、さらに磁場はz方向に一定と考えられるため\(\vec{B}_{\ell_{3}}(\vec{r})\)は
\begin{align}
\vec{B}_{\ell_{3}}(\vec{r})=|\vec{B}_{\ell_{3}}(\vec{r})|(0,0,1) \label{bell3}\tag{16}
\end{align}
としてよい。
よって(\ref{bell1})~(\ref{bell3})を(\ref{soreamp1})に代入して整理していくと、
\begin{align}
\int_{C}\vec{B}(\vec{r})\cdot d\vec{s}&=\int_{\ell_{1}}\vec{B}_{\ell_{1}}(\vec{r})\cdot d\vec{s}_{\ell_{1}}+\int_{\ell_{3}}\vec{B}_{\ell_{3}}(\vec{r})\cdot d\vec{s}_{\ell_{3}}\\
&=\int_{0}^{z_{1}}\mu_{0}nI(0,0,1)\cdot dz(0,0,1)+\int_{0}^{z_{1}}|\vec{B}_{\ell_{3}}(\vec{r})|(0,0,1)\cdot dz(0,0,-1)\\
&=\mu_{0}nI\int_{0}^{z_{1}}dz-|\vec{B}_{\ell_{3}}(\vec{r})|\int_{0}^{z_{1}}dz\\
&=\mu_{0}nIz_{1}-|\vec{B}_{\ell_{3}}(\vec{r})|z_{1} \label{soreamp2}\tag{17}
\end{align}
となる。
よって積分経路\(C\)内に電流は存在しないため、(\ref{am})の右辺は0となり、結局
\begin{gather}
\mu_{0}nIz_{1}-B_{\ell_{3}}z_{1}=0\\
|\vec{B}_{\ell_{3}}(\vec{r})|=\mu_{0}nI \label{sorenaib}\tag{18}
\end{gather}
となる。
(\ref{sorenaib})は、ソレノイド内部で\(x_{1},z_{1}\)を任意にとっても成立するため、ソレノイド内部では磁場は
\begin{align}
\boxed{\vec{B}_{\text{in}}(\vec{r})=\mu_{0}nI(0,0,1)}
\end{align}
で一様であることがわかる。
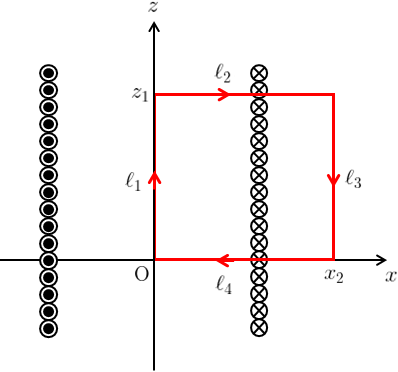
(b) ソレノイド外部の場合
図7の積分経路を、図8の赤色の長方形のようにソレノイドの外側まで拡張する。
ソレノイド内部と同様に考えると、(\ref{am})の左辺の計算結果はソレノイド内部と全く同じになる。
\begin{align}
\int_{C}\vec{B}(\vec{r})\cdot d\vec{s}=\mu_{0}nIz_{1}-|\vec{B}_{\ell_{3}}(\vec{r})|z_{1} \label{soregai1}\tag{19}
\end{align}
ただし今回は積分経路内を電流が貫いているため、(\ref{am})の右辺が値を持つ。
積分経路\(C\)を貫く電流は\(nIz_{1}\)であるため、これを(\ref{am})の右辺に代入すれば
\begin{gather}
\mu_{0}nIz_{1}-|\vec{B}_{\ell_{3}}(\vec{r})|z_{1}=\mu_{0}nIz_{1}\\
|\vec{B}_{\ell_{3}}(\vec{r})|=0 \label{soregaib}\tag{20}
\end{gather}
となる。
(\ref{soregaib})は、ソレノイド外部で\(x_{2},z_{1}\)を任意にとっても成立するため、ソレノイド外部では磁場は存在しないことがわかる。
\begin{align}
\boxed{\vec{B}_{\text{out}}(\vec{r})=\vec{0}}
\end{align}
終わりに
これで、ビオ・サバールの法則とアンペールの法則を使う典型問題をあらかた扱えたと思う。
ここまで長かったが、最後にマクスウェル方程式を使って真空中での電磁波を導出し、電磁気学の記事を一旦締めたい。
END
※追記
マクスウェル方程式から真空中の電磁波を導出。




コメント