前回まで回帰分析、分類と一貫して、正解データからモデルを作る教師あり学習を扱ってきた。
今回から、正解データが存在しないところからモデルを作る教師なし学習の記事執筆に入る。
まずは教師あり学習の分類に似たクラスタリングから。
実装例
早速だが、クラスタリングの実装例を示す。
# モジュールのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import sklearn
from sklearn.cluster import KMeans
# データセットのインポート
file=pd.read_csv('k-means.csv')
# データの割り振り
X=file.iloc[:,0:2]
# 学習実行
# インスタンスの作成
model = KMeans(n_clusters=4,
init='k-means++',
n_init=5,
max_iter=10,
random_state=0)
# モデルの作成
model.fit(X)
# データからの予測値
pred = model.predict(X)
# データセットおよび領域の図示開始
plt.figure(figsize=(4,4))
# カテゴリー領域の図示
x_min = X.iloc[:, 0].min() - 0.5 # 格子点のx座標最小値
x_max = X.iloc[:, 0].max() + 0.5 # 格子点のx座標最大値
y_min = X.iloc[:, 1].min() - 0.5 # 格子点のy座標最小値
y_max = X.iloc[:, 1].max() + 0.5 # 格子点のy座標最大値
h = 0.02 # 格子点生成のステップ数
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) # 格子点生成
Z = model.predict(np.c_[xx.ravel(), yy.ravel()]) # 格子点全点の予測値算出
Z = Z.reshape(xx.shape) # 予測値の配列の形状をxx(yy)の形状に変更
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired) # 領域を図示
# データおよびセントロイドの図示
plt.scatter(X.iloc[:, 0], X.iloc[:, 1], c=pred , edgecolors='k', cmap=plt.cm.Paired , label='Datas')
plt.scatter(model.cluster_centers_[:,0], model.cluster_centers_[:,1],edgecolors='k', marker="*", label="Centroids", s=300, linewidth=1, color='yellow')
# 軸ラベルおよび凡例の表示
plt.xlabel('x')
plt.ylabel('y')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0, fontsize=14)
#図示
plt.show()ただし、「#」以降の記述はコメントであり、プログラムに直接影響はしない。
上記プログラムを実行すると、例えば次のような図が出力される。
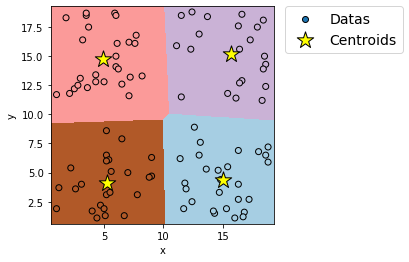
上記プログラムは何をしているかというと、
① データのインポート
x-y座標上の点のデータをインポートする。
② 学習(分類の実行)
k-means法を利用して、x-y座標上の点を4つのグループ(クラスタ)に分類する。
③ 学習の確認
x-y座標上の点と学習で得られた4つのグループの領域を図示し、学習が適切に実行されているか確認する。
といったことをしている。
実際にプログラムを実行したい場合は、下記ボタンよりcsvファイル「k-means.csv」をダウンロードしてプログラムの保存先に保存すること。
クラスタリング概説
早速聞きなれない単語がいくつか出てきたので、ここで簡単に解説する。
クラスタリングとは、類似している複数のデータをまとめることである。
クラスタリングの結果生まれるデータの集まりをクラスタ(cluster)と呼ぶ。
ここだけ聞くと、ロジスティック回帰や決定木のような分類と同じだが、決定的な違いは「正解が与えられていないこと」である。
分類では、このデータはグループ1、このデータはグループ2というようにデータがすでに分類されている状態だったが、クラスタリングではデータはどこにも分類されていない状態から学習がスタートする。
そのため、データをいくつのクラスタにわけるのか、クラスタリングした結果が妥当なのかという判断は人間が実施する必要がある。
クラスタリングのアルゴリズムの中で、代表的なものがk-means法(k平均法)である。
k-means法では下記の手順でクラスタリングが実施される。
① 全データの中から、k個のデータをランダムに選ぶ。
このk個のデータをセントロイドと呼ぶ。
② 残りのデータそれぞれと、各セントロイドまでの距離を調べる。
③ 最も近いセントロイドが同じもの同士でグループを作る。
例えば、データ1とデータ2が同じセントロイド1に最も近いなら、データ1と2は同じグループに振り分ける。
④ ③で生成されたグループの内、各グループの重心に位置するデータを新たなセントロイドとする。
⑤ ②~④を繰り返し、適当なところで繰り返しを終了する。
終了するタイミングは、基本的には下記2パターンに分かれる。
(1) ③での振り分け結果が前回の結果と同じだった場合
(2) 人間側が指定した繰り返し回数に達した場合
下記に続く。





コメント