前回
の続き。
前回の内容を踏まえ、今記事から具体的な問題を解いていく。
問題1
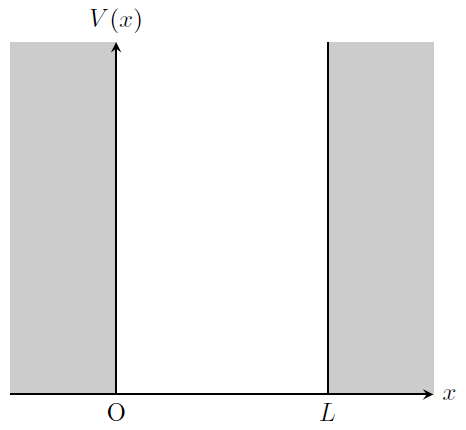
右図のように、\(x=0, L\)に無限大のポテンシャル障壁があり、その内部にある自由粒子を考える。
\begin{align}
V(x)= \begin{cases} 0\qquad (0\leq x \leq L) \\
\infty\qquad (x<0,\,x>L)
\end{cases}
\end{align}
このとき、この粒子に関する定常状態のシュレディンガー方程式を立て、その解(つまり、波動関数とエネルギー固有値)をすべて求めよ。
ただし、波動関数は規格化すること。
解答
まず、各領域に応じて一次元自由粒子の定常状態のシュレディンガー方程式を立てる。
今回の系では\(x<0,\,x>L\)に無限大のポテンシャル障壁があるため、 \(x<0,\,x>L\)には粒子は存在しえない。よって、 \(x<0,\,x>L\)でシュレディンガー方程式を立てる必要なない。
\(0\leq x \leq L\)では外部ポテンシャルが存在しないため、シュレディンガー方程式は
\begin{align}
-\frac{\hbar^{2}}{2m}\frac{d^{2}}{dx^{2}}\varphi(x)=E\varphi(x) \tag{1}\label{自由粒子シュレ}
\end{align}
と書ける。(\ref{自由粒子シュレ})は典型的な微分方程式であり、本来なら\(E\)の符号によって場合分けが必要だが、外部ポテンシャルの最小値\(V_{\text{min}}=0\)であるため\(E\geq 0\)となる。(前回記事のルール②を参照。)
よって\(k=\sqrt{2mE/\hbar^2} \)とすると、\(-k<0\)であるため、(\ref{自由粒子シュレ})の一般解は\(C,D\)を任意定数として
\begin{align}
\varphi(x)=C\cos(kx)+D\sin(kx) \tag{2}\label{E>0の一般解}
\end{align}
となる。
ここから、境界条件、接続条件、規格化条件を使って任意定数\(C,D\)とエネルギー固有値\(E\)を決定する。
今回は粒子が存在し得る領域が1つしかないため、接続条件は考えなくてよい。
境界条件は、\(x<0,\,x>L\)に無限大のポテンシャル障壁があるため、
\begin{align}
\varphi(0)=\varphi(L)=0 \tag{3}\label{境界条件}
\end{align}
となる。この(\ref{境界条件})に(\ref{E>0の一般解})を代入すると、次の2式が得られる。
\begin{align}
&C=0 \tag{4}\label{phi0} \\
&C\cos(kL)+D\sin(kL)=0 \tag{5}\label{phil}
\end{align}
よって(\ref{phi0})を(\ref{phil})に代入すれば
\begin{align}
\sin(kL)=0 \qquad \therefore k=\frac{n\pi}{L}\quad(n\in\mathbb{Z}) \tag{6}\label{k}
\end{align}
が得られ、さらに\(k=\sqrt{2mE/\hbar^2} \)を思い出せば、エネルギー固有値が下記のように求められる。
\begin{align}
E=\frac{\pi^{2}\hbar^{2}}{2mL^{2}}n^{2}\quad (n\in\mathbb{Z}) \tag{7}\label{E1}
\end{align}
さらに(\ref{phi0})を(\ref{E>0の一般解})に代入して、
\begin{align}
\varphi(x)=D\sin(kx) \tag{8}\label{解1}
\end{align}
が得られる。よって規格化条件より、
\begin{align}
\int_{0}^{L}|\varphi(x)|^{2}dx=D^{2} \int_{0}^{L}\sin(kx)^{2}dx=\frac{D^{2}L}{2}=1 \qquad\therefore D=\pm\sqrt{\frac{2}{L}} \tag{9}\label{A}
\end{align}
となる。よって(\ref{k})と(\ref{A})を(\ref{解1})に代入すれば、
\begin{align}
\varphi(x)=\pm\sqrt{\frac{2}{L}}\sin\left( \frac{n\pi}{L}x\right)\quad (n\in\mathbb{Z}) \tag{10}
\end{align}
と求められる。
ここから解の絞り込みを行う。
まず、\(n=0\)のときは全領域で\(\varphi(x)=0\)となり、規格化条件を満たさないため物理的に不適である。
また定数倍のルールより、定数\(D\)の符号はどちらをとっても構わない。今回は\(D=\sqrt{2/L}\)を採用する。
さらに\(n>0\)のとき、
\begin{align}
\varphi_{-n}(x)= \sqrt{\frac{2}{L}}\sin\left( -\frac{n\pi}{L}x\right)=-\sqrt{\frac{2}{L}}\sin\left( \frac{n\pi}{L}x\right)=-\varphi_{n}(x) \tag{11}
\end{align}
となり、定数倍のルールから\(\pm n\)では物理的状態が同じであることがわかる。よって\(n\)の範囲は自然数までで十分である。
以上より、求める波動関数およびエネルギー固有値は\(n\in\mathbb{N}\)として、
\begin{align}
\begin{cases}
波動関数:\displaystyle{\varphi_{n}(x)= \sqrt{\frac{2}{L}}\sin\left( \frac{n\pi}{L}x\right)} \\
エネルギー固有値:\displaystyle{E_{n}= \frac{\pi^{2}\hbar^{2}}{2mL^{2}}n^{2} }
\end{cases}
\end{align}
となる。
終わりに
今回は解析的にすべての定数を求めることができたが、こういったパターンはかなり限られる。
次回から早速、解析的にはすべて解けない問題を扱っていこうと思う。
続きはこちら。





コメント