シュレディンガー方程式から波動関数とエネルギー固有値を求めることで、その系の量子力学的状態を求めることができる。
その状態の数え方として、あるエネルギー固有値以下の状態を数える状態数という考え方がある。
考え方はそこまで難しくないのだが、論文や本によって定義の仕方が異なっている場合があり、それが混乱を生じるもととなることがある。
本記事ではそういった混乱を解消することを目的として、状態数と状態密度について見ていく。
状態数と状態密度
状態数(number of states)\(\Omega(E)\)とは、あるエネルギー\(E\)以下のエネルギーをもつ状態の総数である。
例として、前回扱ったの箱型ポテンシャル中の自由粒子を考える。
簡単に復習すると、箱型ポテンシャル中に閉じ込められた質量\(m\)の自由粒子がとりうる状態を調べたとき、波動関数\(\varphi(\vec{r})\)と全体のエネルギー\(E\)は\(n_{x},n_{y},n_{z}\in\mathbb{N}\)として
\begin{align}
&\varphi(\vec{r})=\left(\frac{2}{L}\right)^{\frac{3}{2}}\sin\left(\frac{n_{x}\pi}{L}x\right)\sin\left(\frac{n_{y}\pi}{L}y\right)\sin\left(\frac{n_{z}\pi}{L}z\right)\tag{1}\label{全体の波動関数} \\
&E=\frac{\pi^{2}\hbar^{2}}{2mL^{2}}(n_{x}^{2}+n_{y}^{2}+n_{z}^{2}) \tag{2}\label{全体のエネルギー}
\end{align}
となるのだった。
ここで、前回に定義した三つの自然数の組\((n_{x},n_{y},n_{z})\)による空間を考える。
この場合、\((n_{x},n_{y},n_{z})\)空間内にある一辺が1の立方体中に、状態が一つ入っているとみなすことができる。
さらにこの系のエネルギー固有値(\ref{全体のエネルギー})を次のように変形する。
\begin{align}
n_{x}^{2}+n_{y}^{2}+n_{z}^{2}=\frac{2mL^{2}E}{\pi^{2}\hbar^{2}} \tag{3}\label{球面の方程式}
\end{align}
(\ref{球面の方程式})は\((n_{x},n_{y},n_{z})\)空間における、半径\(\sqrt{2mL^{2}E/(\pi^{2}\hbar^{2})}\)の球面の方程式になっている。
よってこの球面内にある一辺が1の立方体の総数が、エネルギー\(E\)以下のエネルギーをもつ状態の総数、すなわち状態数に対応していることがわかる。
(球面内の格子点\((n_{x},n_{y},n_{z})\)の総数が、状態数の総数に対応していると考えてもよい。)
よって\((n_{x},n_{y},n_{z})\)が全て自然数であることに注意すれば、求める状態数は半径\(\sqrt{2mL^{2}E/(\pi^{2}\hbar^{2})}\)の球の体積の1/8となる(下図を参照)。
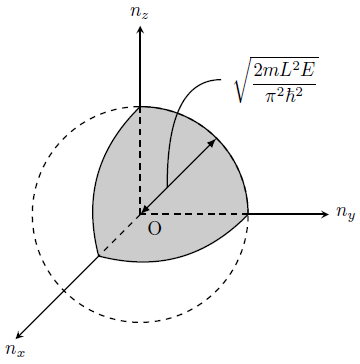
すなわち
\begin{align}
\Omega(E)&=\frac{4}{3}\pi\left(\sqrt{\frac{2mL^{2}E}{\pi^{2}\hbar^{2}}}\right)^{3}\times\frac{1}{8}\\
&=\frac{\pi}{6}\left(\frac{2mL^{2}E}{\pi^{2}\hbar^{2}}\right)^{\frac{3}{2}}=\frac{\pi}{6}\frac{(2m)^{\frac{3}{2}}}{\pi^{3}\hbar^{3}}L^{3}E^{\frac{3}{2}}=\frac{(2m)^{\frac{3}{2}}}{6\pi^{2}\hbar^{3}}VE^{\frac{3}{2}} \tag{4}\label{状態数}
\end{align}
となる。ただし\(V=L^{3}\)は立方体の体積である。
補足
立方体の体積で球の体積をそうすんなりと書き表して良いのかというのは当然の疑問だと思う。
実際はエネルギー\(E\)を十分大きくとれば、(\ref{状態数})の結果は良い近似となる。
さらにこの\(\Omega(E)\)をエネルギー\(E\)で微分した導関数\(D(E)\)を考える。
すなわち
\begin{align}
D(E)=\frac{d}{dE}\Omega(E)=\frac{(2m)^{\frac{3}{2}}}{6\pi^{2}\hbar^{3}}V\left(\frac{d}{dE}E^{\frac{3}{2}}\right)=\frac{(2m)^{\frac{3}{2}}}{6\pi^{2}\hbar^{3}}V\frac{3}{2}E^{\frac{1}{2}}=\frac{(2m)^{\frac{3}{2}}}{4\pi^{2}\hbar^{3}}V\sqrt{E} \tag{5}
\end{align}
である。
この\(D(E)\)が状態密度(density of states)である。
この\(D(E)\)を体積\(V\)で割れば、単位体積当たりの状態密度\(\nu(E)\)を求めることができ
\begin{align}
\nu(E)=\frac{D(E)}{V}=\frac{(2m)^{\frac{3}{2}}}{4\pi^{2}\hbar^{3}}\sqrt{E} \tag{6}
\end{align}
となる。
空間の定義による違い
ここまでは\((n_{x},n_{y},n_{z})\)空間を考えたが、先述した通り、エネルギー\(E\)を指定する量であれば、空間を定義する量は何でもよい。
事実、論文や教科書によっては波数空間\((k_{x},k_{y},k_{z})\)や運動量空間\((p_{x},p_{y},p_{z})\)で状態数を計算しているものもある。
しかし結局は、波数空間の場合は
\begin{align}
k_{x}^{2}+k_{y}^{2}+k_{z}^{2}=\frac{\pi^{2}}{L^{2}}(n_{x}^{2}+n_{y}^{2}+n_{z}^{2})=\frac{2mE}{\hbar^{2}} \tag{7}
\end{align}
の球面の方程式を考えて、この球面内における一辺が\(\pi/L\)の立方体の総数を考えればよく、運動量空間の場合は
\begin{align}
p_{x}^{2}+p_{y}^{2}+p_{z}^{2}=\frac{\pi^{2}\hbar^{2}}{L^{2}}(n_{x}^{2}+n_{y}^{2}+n_{z}^{2})=2mE \tag{8}
\end{align}
の球面の方程式を考えて、この球面内における一辺が\(\pi\hbar/L\)の立方体の総数を考えればよい。
本質的な考え方は、結局\((n_{x},n_{y},n_{z})\)空間と同じである。
また分野によっては、一辺がプランク定数\(h\)の立方体中に状態が一つ入っているとみなす位相空間(phase space)が使われていることもある。
位相空間においては、
\begin{align}
h^{2}(n_{x}^{2}+n_{y}^{2}+n_{z}^{2})=2\pi^{2}\hbar^{2}(n_{x}^{2}+n_{y}^{2}+n_{z}^{2})=4mL^{2}E \tag{9}
\end{align}
という球面の方程式を考えればよく、\((n_{x},n_{y},n_{z})\)空間と同様に考えて、
\begin{align}
\Omega(E)=\frac{4}{3}\pi\left(\sqrt{4mL^{2}E}\right)^{3}\times\frac{1}{8}\div h^{3} \tag{10}
\end{align}
となる。
ここで運動量の大きさを\(p=\sqrt{p_{x}^{2}+p_{y}^{2}+p_{z}^{2}}\)とすると\(p^{2}=2mE\)より
\begin{align}
\Omega(E)&=\frac{4}{3}\pi\left(\sqrt{2p^{2}L^{2}}\right)^{3}\times\frac{1}{8}\div h^{3}\\
&=\frac{4}{3}\pi2^{\frac{3}{2}}p^{3}L^{3}\times\frac{1}{8}\div h^{3}=\frac{\sqrt{2}}{3}\pi p^{3}V\div h^{3}\simeq1.5\frac{p^{3}V}{h^{3}}\tag{11}
\end{align}
となる。
終わりに
波数空間や位相空間など、言葉だけ見るととっつきにくい印象を覚えるかもしれないが、基本的な考え方は通常の状態数を求めるときと変わらない。
書籍や論文で扱う軸が異なれば、自分で扱いやすい軸に合わせてしまえば問題ない。
自分自身がこれに気づいたときはそこそこ嬉しかったのだが、同じようなことを思ってくれる人がいたら幸いだ。
END





コメント