前回
に引き続き、具体的な問題を解いていく。
ただし、今回からはシュレディンガー方程式を完璧に解くことはせず、ある程度物理的考察ができるところまで解き進めたらストップすることにする。
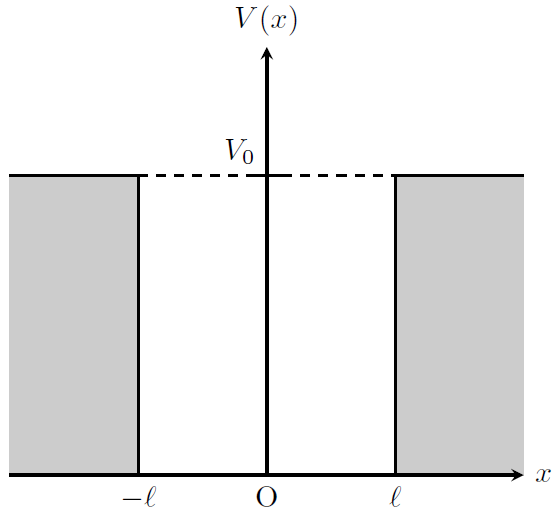
問題2
\begin{align}
V(x)=
\begin{cases}
0\qquad (|x|\leq \ell) \\
V_{0}\qquad (|x|>\ell)
\end{cases}
\end{align} このとき、この粒子に関する定常状態のシュレディンガー方程式を立て、波動関数を任意定数を1つまで絞った形で求め、エネルギー固有値\(E\)を決める条件式を
(a)\(x\)の反転に対して対称な解
(b)\(x\)の反転に対して反対称な解
それぞれについて求めよ。
ただし下記事項を利用してよい。
①\(\varepsilon=2mE/\hbar^{2},\,v_{0}=2mV_{0}/\hbar^{2}\)
②無限遠方では粒子は存在しない。
③一変数関数\(f(x)\)とその導関数\(f'(x)\)が連続であるとき、\(f'(x)/f(x)\)もまた連続である。
解答(a)
まず、各領域に応じて一次元自由粒子の定常状態のシュレディンガー方程式を立てる。
まず、\(|x|\leq \ell\)では外部ポテンシャルが存在しないため、シュレディンガー方程式は
\begin{align}
-\frac{\hbar^{2}}{2m}\frac{d^{2}}{dx^{2}}\varphi(x)=E\varphi(x) \tag{1}\label{自由粒子シュレ}
\end{align}
と書ける。前回と同様に考えると、\(\varepsilon=2mE/\hbar^2>0\)、 \(C,D\)を任意定数として、(\ref{自由粒子シュレ})の解は
\begin{align}
\varphi(x)=C\cos( \sqrt{\varepsilon} x )+D\sin( \sqrt{\varepsilon} x )\quad(|x|\leq\ell) \tag{2}\label{E>0の一般解}
\end{align}
となる。
次に\(|x|>\ell\)の領域だが、ここでは有限のポテンシャル障壁\(V(x)=V_{0}\)が存在するため、シュレディンガー方程式は
\begin{align}
-\frac{\hbar^{2}}{2m}\frac{d^{2}}{dx^{2}}\varphi(x)+V_{0}\varphi(x) =E\varphi(x) \tag{3}\label{V0シュレ}
\end{align}
となる。(\ref{V0シュレ})を解く際には\(E<V_{0}\)の場合と\(E\geq V_{0}\)の場合で場合分けが必要になる。しかし、\(E\geq V_{0}\)の場合は振動解となり、\(\int_{-\infty}^{\infty}|\varphi(x)|^{2}dx=\infty\)となって規格化条件を満たさない。
よって \(E<V_{0}\) の場合のみ考えればよく、\(v_{0}=2mV_{0}/\hbar^2\)、\(A,B,F,G\)を任意定数として、(\ref{V0シュレ})の解は
\begin{align}
&\varphi(x)=Ae^{\sqrt{v_{0}-\varepsilon} x}+Be^{- \sqrt{v_{0}-\varepsilon} x}\quad(x<-\ell) \tag{4}\label{x-ellの一般解}\\
&\varphi(x)=Fe^{\sqrt{v_{0}-\varepsilon} x}+Ge^{- \sqrt{v_{0}-\varepsilon} x}\quad(x>\ell) \tag{5}\label{xellの一般解}
\end{align}
となる。
さらにここで、無限遠方では粒子は存在しないという境界条件を課す(②)。すなわち\(\displaystyle{\lim_{|x|\to\infty}\varphi(x)=0}\)を要請すると、\(B=F=0\)となる。
ここで求めた解をまとめておく。
\begin{align}
\varphi(x)=
\begin{cases}
Ae^{\sqrt{v_{0}-\varepsilon} x} &\quad(x<-\ell) \\
C\cos( \sqrt{\varepsilon} x )+D\sin( \sqrt{\varepsilon} x ) &\quad(|x|\leq\ell) \\
Ge^{- \sqrt{v_{0}-\varepsilon} x}&\quad(x>\ell) \tag{6}\label{解1}
\end{cases}
\end{align}
ここから本格的に、\(x\)の反転に対して対称な解について考える。
今回の系では外部ポテンシャルが対称(\(V(x)=V(-x)\))であるため、波動関数が対称または反対称のいずれかにとることができる。
対称な解、すなわち\(\varphi(x)=\varphi(-x)\)となる解を考えると(\ref{解1})は下記のように書き換えられる。
\begin{align}
\varphi(x)=
\begin{cases}
Ae^{\sqrt{v_{0}-\varepsilon} x} &\quad(x<-\ell) \\
C\cos( \sqrt{\varepsilon} x ) &\quad(|x|\leq\ell) \\
Ae^{- \sqrt{v_{0}-\varepsilon} x}&\quad(x>\ell) \tag{7}\label{対称解}
\end{cases}
\end{align}
ここで接続条件を考える。今回は\(x\)の反転に対して対称な解であるため、片方のみを考えればよい。そこで\(x=\ell\)での接続を考えると、
\begin{align}
&\varphi(\ell)\,:\, C\cos( \sqrt{\varepsilon}\,\ell)=Ae^{- \sqrt{v_{0}-\varepsilon}\,\ell} \tag{8}\label{対称phi接続}\\
&\varphi'(\ell)=\frac{d\varphi(x)}{dx}\bigg|_{x=\ell}\,:\, -C \sqrt{\varepsilon} \sin( \sqrt{\varepsilon}\,\ell)=-A \sqrt{v_{0}-\varepsilon}\,e^{- \sqrt{v_{0}-\varepsilon}\,\ell} \tag{9}\label{対称phi’接続}
\end{align}
が得られる。
また\(\varphi(x)\)とその導関数\( \varphi ‘(x)\)が連続であるとき、\( \varphi ‘(x)/ \varphi (x)\)もまた連続である(③)。 よって(\ref{対称phi接続})と(\ref{対称phi’接続})より
\begin{gather}
\frac{ -C \sqrt{\varepsilon} \sin( \sqrt{\varepsilon}\,\ell) }{ C\cos( \sqrt{\varepsilon}\,\ell) }= \frac{ -A \sqrt{v_{0}-\varepsilon}\,e^{- \sqrt{v_{0}-\varepsilon}\,\ell} }{ Ae^{- \sqrt{v_{0}-\varepsilon}\,\ell} } \\
\tan( \sqrt{\varepsilon}\,\ell )=\sqrt{\frac{v_{0}-\varepsilon}{\varepsilon}} \\
\therefore \tan\left( \sqrt{\frac{2mE}{\hbar^2} }\,\ell \right)= \sqrt{\frac{V_{0}-E}{E}} \tag{10}\label{対称E}
\end{gather}
が得られる。この(\ref{対称E})が対称解においてエネルギー固有値\(E\)を決める条件式である。
また、(\ref{対称phi接続})を(\ref{対称解})に代入すれば、波動関数を任意定数を1つまで絞った形で求められる。
以上より、\(x\)の反転に対して対称な解については下記のようになる。
\begin{align}
&波動関数:\varphi(x)=
\begin{cases}
C\cos(\sqrt{\varepsilon}\,\ell)e^{\sqrt{v_{0}-\varepsilon}\,(x+\ell)} &\quad(x<-\ell) \\
C\cos( \sqrt{\varepsilon} x ) &\quad(|x|\leq\ell) \\
C\cos(\sqrt{\varepsilon}\,\ell)e^{- \sqrt{v_{0}-\varepsilon}\,(x-\ell)}&\quad(x>\ell) \tag{11}\label{対象解最終}
\end{cases}\\
&\quad\\
&エネルギー固有値:\tan\left( \sqrt{\frac{2mE}{\hbar^2} }\,\ell \right)= \sqrt{\frac{V_{0}-E}{E}} \tag{12}\label{対称E最終}
\end{align}
解答(b)
\(x\)の反転に対して反対称な解、すなわち\(\varphi(x)=-\varphi(-x)\)となる解を考えると(\ref{解1})は下記のように書き換えられる。
\begin{align}
\varphi(x)=
\begin{cases}
-Ae^{\sqrt{v_{0}-\varepsilon} x} &\quad(x<-\ell) \\
D\sin( \sqrt{\varepsilon} x ) &\quad(|x|\leq\ell) \\
Ae^{- \sqrt{v_{0}-\varepsilon} x}&\quad(x>\ell) \tag{14}\label{反対称解}
\end{cases}
\end{align}
ここで接続条件を考える。\(x\)の反転に対して反対称な解であるため、今回も片方のみを考えればよい。そこで\(x=\ell\)での接続を考えると、
\begin{align}
&\varphi(\ell)\,:\, D\sin( \sqrt{\varepsilon}\,\ell)=Ae^{- \sqrt{v_{0}-\varepsilon}\,\ell} \tag{15}\label{反対称phi接続}\\
&\varphi'(\ell)=\frac{d\varphi(x)}{dx}\bigg|_{x=\ell}\,:\, D \sqrt{\varepsilon} \cos( \sqrt{\varepsilon}\,\ell)=-A \sqrt{v_{0}-\varepsilon}\,e^{- \sqrt{v_{0}-\varepsilon}\,\ell} \tag{16}\label{反対称phi’接続}
\end{align}
が得られる。
また\(\varphi(x)\)とその導関数\( \varphi ‘(x)\)が連続であるとき、\( \varphi ‘(x)/ \varphi (x)\)もまた連続である(③)。 よって(\ref{反対称phi接続})と(\ref{反対称phi’接続})より
\begin{gather}
\frac{ D\sqrt{\varepsilon} \cos( \sqrt{\varepsilon}\,\ell) }{ D\sin( \sqrt{\varepsilon}\,\ell) }= \frac{ -A \sqrt{v_{0}-\varepsilon}\,e^{- \sqrt{v_{0}-\varepsilon}\,\ell} }{ Ae^{- \sqrt{v_{0}-\varepsilon}\,\ell} } \\
\frac{1}{\tan( \sqrt{\varepsilon}\,\ell )}=-\sqrt{\frac{v_{0}-\varepsilon}{\varepsilon}} \\
\therefore \tan\left( \sqrt{\frac{2mE}{\hbar^2} }\,\ell \right)= -\sqrt{\frac{E}{V_{0}-E}} \tag{17}\label{反対称E}
\end{gather}
が得られる。この(\ref{反対称E})が反対称解においてエネルギー固有値\(E\)を決める条件式である。
また、(\ref{反対称phi接続})を(\ref{反対称解})に代入すれば、波動関数を任意定数を1つまで絞った形で求められる。
以上より、\(x\)の反転に対して対称な解については下記のようになる。
\begin{align}
&波動関数:\varphi(x)=
\begin{cases}
-D\sin(\sqrt{\varepsilon}\,\ell)e^{\sqrt{v_{0}-\varepsilon}\,(x+\ell)} &\quad(x<-\ell) \\
D\sin( \sqrt{\varepsilon} x ) &\quad(|x|\leq\ell) \\
D\sin(\sqrt{\varepsilon}\,\ell)e^{- \sqrt{v_{0}-\varepsilon}\,(x-\ell)}&\quad(x>\ell) \tag{18}\label{反対称解最終}
\end{cases}\\
&\quad\\
&エネルギー固有値:\tan\left( \sqrt{\frac{2mE}{\hbar^2} }\,\ell \right)= -\sqrt{\frac{E}{V_{0}-E}} \tag{19}\label{反対称E最終}
\end{align}
考察
すべての解をまとめてみると、下記のようになる。
対称解
\begin{align}
&波動関数:\varphi_{対称}(x)=
\begin{cases}
C\cos(\sqrt{\varepsilon}\,\ell)e^{\sqrt{v_{0}-\varepsilon}\,(x+\ell)} &\quad(x<-\ell) \\
C\cos( \sqrt{\varepsilon} x ) &\quad(|x|\leq\ell) \\
C\cos(\sqrt{\varepsilon}\,\ell)e^{- \sqrt{v_{0}-\varepsilon}\,(x-\ell)}&\quad(x>\ell)
\end{cases}\\
&\quad\\
&エネルギー固有値:\tan\left( \sqrt{\frac{2mE_{対称}}{\hbar^2} }\,\ell \right)= \sqrt{\frac{V_{0}-E_{対称}}{E_{対称}}}
\end{align}
反対称解
\begin{align}
&波動関数:\varphi_{反対称}(x)=
\begin{cases}
-D\sin(\sqrt{\varepsilon}\,\ell)e^{\sqrt{v_{0}-\varepsilon}\,(x+\ell)} &\quad(x<-\ell) \\
D\sin( \sqrt{\varepsilon} x ) &\quad(|x|\leq\ell) \\
D\sin(\sqrt{\varepsilon}\,\ell)e^{- \sqrt{v_{0}-\varepsilon}\,(x-\ell)}&\quad(x>\ell)
\end{cases}\\
&\quad\\
&エネルギー固有値:\tan\left( \sqrt{\frac{2mE _{反対称} }{\hbar^2} }\,\ell \right)= -\sqrt{\frac{E _{反対称} }{V_{0}-E _{反対称} }}
\end{align}
ここで、\(V_{0}\to\infty\)の極限を考えてみよう。
まず対称解を見ると、\(|x|>\ell\)の波動関数はともに0になる。
またエネルギー固有値を決定する式の右辺が無限大に発散するため、
\begin{gather}
\sqrt{\frac{2mE_{対称}}{\hbar^2} }\,\ell =\frac{n_{対称}\pi}{2}\\
\therefore E_{対称}=\frac{\pi^{2}\hbar^{2}}{2m(2\ell)^{2}}n_{対称}^{2}\quad(n_{対称}=1,3,5,…)
\end{gather}
となる。
続いて反対称解も考えると、こちらも\(|x|>\ell\)の波動関数はともに0になる。
エネルギー固有値を決定する式の右辺は0に向かうため、
\begin{gather}
\sqrt{\frac{2mE_{反対称}}{\hbar^2} }\,\ell =\frac{n_{反対称}\pi}{2}\\
\therefore E_{反対称}=\frac{\pi^{2}\hbar^{2}}{2m(2\ell)^{2}}n_{反対称}^{2}\quad(n_{反対称}=2,4,6…)
\end{gather}
となる。
\(n_{反対称}=0\)のとき、波動関数が全領域で0となるため規格化条件を満たさず、物理的に不適である。
結局、両方のエネルギー固有値を組み合わせれば、
\begin{align}
E_{n}=\frac{\pi^{2}\hbar^{2}}{2m(2\ell)^{2}}n^{2}\quad(n\in\mathbb{N})
\end{align}
となり、以前扱った無限大のポテンシャル障壁に挟まれた自由粒子のエネルギー固有値に対応することがわかる。
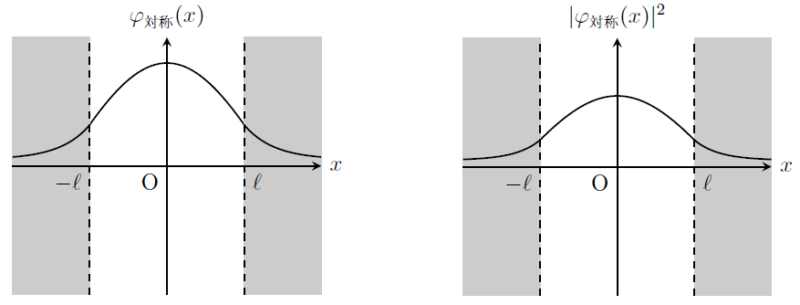
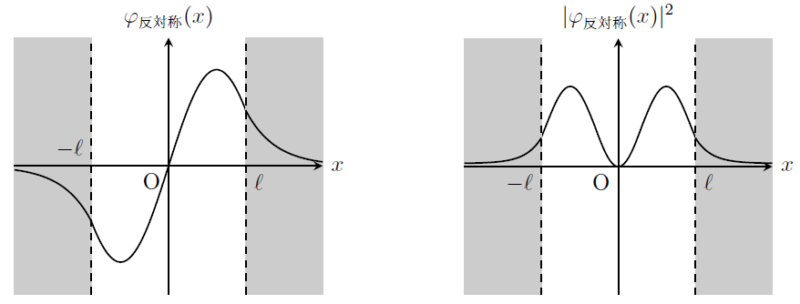
また、対称解および反対称解それぞれの内で最も単純な波動関数\(\varphi(x)\)と確率密度\(|\varphi(x)|^{2}\)のグラフも示しておく。
対称解
反対称解
ここで、今回求めた解がすべて\(E<V_{0}\)を前提にしていることを思い出すと、奇妙なことが起きていることに気づく。
確率密度\(|\varphi(x)|^{2}\)は、粒子が位置\(x\)に存在する確率の分布を与える。
ポテンシャル障壁が存在しない\(|x|\leq\ell\)で\(|\varphi(x)|^{2}\)が有限の値を持つことは理解できるが、注目すべきは、ポテンシャル障壁中の\(|x|>\ell\)でも\(|\varphi(x)|^{2}\)が有限の値を持つことだ。
これは古典論ではありえない現象である。
古典論では有限のポテンシャル障壁を乗り越えるには、その障壁以上のエネルギーを有していなければならないからだ。
しかし今回得られた結果は、量子力学では、粒子が持つエネルギーがポテンシャル障壁以下の値でも、ポテンシャル障壁が占める領域に粒子が存在し得ることを示している。
終わりに
量子力学では、ポテンシャル障壁よりエネルギー値が小さくても、ポテンシャル障壁が占める領域に粒子が存在し得ることがわかった。
今回の問題設定では、ポテンシャル障壁が無限遠まで続くため、粒子の存在確率は原点から離れるにつれて小さくなるだけで、終いには0に収束する。
では、このポテンシャル障壁が占める領域が有限である場合はどうなるだろう?
次回からいよいよ、本テーマの本命であるトンネル効果を扱っていく。
続きはこちら。





コメント