前回
からの続き。
今までは1変数関数のマクローリン展開を中心に見てきたが、今回は多変数関数のマクローリン展開を扱う。
ただし計算が複雑になるので、今回は例は簡単なものに留めておく。
多変数関数の場合の一般論
任意の\(n\)変数関数\(f(x_{1},x_{2},…,x_{n})\)のマクローリン展開は
\begin{align}
f(x_{1},x_{2},…,x_{n})=\sum_{k=0}^{\infty}\frac{1}{k!}\left.\left(\sum_{i=1}^{n}x_{i}\frac{\partial}{\partial x_{i}}\right)^{k}f(x_{1},x_{2},…,x_{n})\right|_{x_{i}=0} \tag{1}\label{多変数関数マクローリン展開}
\end{align}
と表される。
特に2変数関数\(f(x,y)\)の場合は
\begin{align}
f(x,y)=\sum_{k=0}^{\infty}\frac{1}{k!}\left.\left(x\frac{\partial}{\partial x}+ y\frac{\partial}{\partial y} \right)^{k}f(x,y)\right|_{x,y=0} \tag{2}\label{2変数関数マクローリン展開}
\end{align}
と書け、2次の項まで展開すると
\begin{align}
f(x,y)=&f(0,0)+\left\{\left.\frac{\partial f(x,y)}{\partial x}\right|_{x,y=0}\right\}x+\left\{\left.\frac{\partial f(x,y)}{\partial y}\right|_{x,y=0}\right\}y \\
&+\frac{1}{2}\left\{\left.\frac{\partial^{2} f(x,y)}{\partial x^{2}}\right|_{x,y=0}\right\}x^{2} \\
&+\frac{1}{2}\left\{\left.\frac{\partial^{2} f(x,y)}{\partial x\partial y}\right|_{x,y=0}+ \left.\frac{\partial^{2} f(x,y)}{\partial y\partial x}\right|_{x,y=0} \right\}xy \\
&+\frac{1}{2}\left\{\left.\frac{\partial^{2} f(x,y)}{\partial y^{2}}\right|_{x,y=0}\right\}y^{2} \tag{3}\label{2変数関数マクローリン展開2}
\end{align}
となる。
例
次の2変数関数を考える。
\begin{align}
f(x,y)=e^{x^{2}+y^{2}} \tag{4}\label{2変数関数例}
\end{align}
この2変数関数\(f(x,y)\)を2次の項までマクローリン展開する。
まず、\(f(x,y)\)の偏微分を計算しておくと、
\begin{align}
&\frac{\partial f(x,y)}{\partial x}=2x\,e^{x^{2}+y^{2}}\\
&\frac{\partial f(x,y)}{\partial y}=2y\,e^{x^{2}+y^{2}}\\
&\frac{\partial^{2} f(x,y)}{\partial x^{2}}=2\,e^{x^{2}+y^{2}}+4x^{2}\,e^{x^{2}+y^{2}} \\
&\frac{\partial^{2} f(x,y)}{\partial y\partial x}=4xy\,e^{x^{2}+y^{2}} \\
&\frac{\partial^{2} f(x,y)}{\partial x\partial y}=4xy\,e^{x^{2}+y^{2}} \\
&\frac{\partial^{2} f(x,y)}{\partial y^{2}}=2\,e^{x^{2}+y^{2}}+4y^{2}\,e^{x^{2}+y^{2}}
\end{align}
となる。よってそれぞれ\(x,y=0\)を代入すると、
\begin{align}
&\left.\frac{\partial f(x,y)}{\partial x}\right|_{x,y=0}=0\\
& \left. \frac{\partial f(x,y)}{\partial y} \right|_{x,y=0} =0\\
& \left. \frac{\partial^{2} f(x,y)}{\partial x^{2}} \right|_{x,y=0} =2 \\
& \left. \frac{\partial^{2} f(x,y)}{\partial y\partial x} \right|_{x,y=0} =0\\
& \left. \frac{\partial^{2} f(x,y)}{\partial x\partial y} \right|_{x,y=0} =0 \\
& \left. \frac{\partial^{2} f(x,y)}{\partial y^{2}} \right|_{x,y=0} =2
\end{align}
となるため、これらを(\ref{2変数関数マクローリン展開2})に代入すれば、
\begin{align}
f(x,y)=1+x^{2}+y^{2} \tag{5}\label{例mac}
\end{align}
が得られる。
さて、本当に(\ref{例mac})が\(x,y=0\)付近で(\ref{2変数関数例})を再現しているか、グラフで確かめてみる。
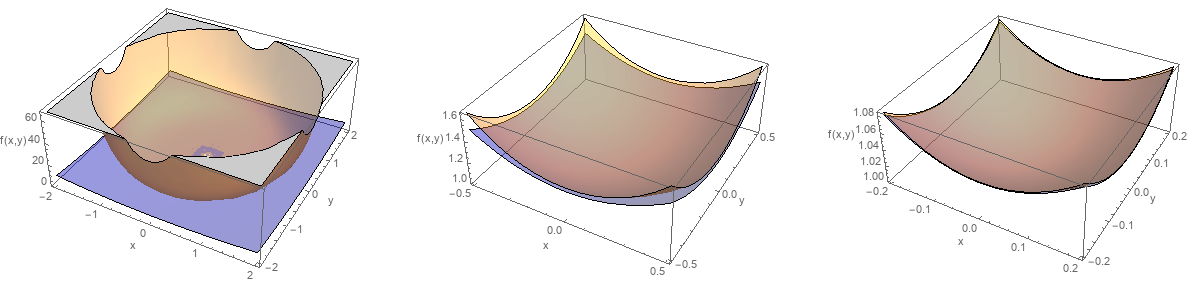
上の3つのグラフにおいて、橙色が(\ref{2変数関数例})、青色が(\ref{例mac})である。
右に向かうに従ってグラフの表示範囲が狭くなっており、それに従って2つのグラフが良い一致を見せているのがわかるだろう。
終わりに
ここでひとまず、テイラー展開とマクローリン展開に関する記事は一区切りつけようと思う。
本当のところを言うと、最初に紹介したテイラー展開とマクローリン展開の公式の右辺は発散する場合があり、必ずしも正しいとは言えない。
だがその話に取り掛かるのは、テイラー展開とマクローリン展開の計算の仕方を身につけてからで問題ない。
(正直言うと、私自身もその辺はまだちゃんと理解していない。)
まずは実際に、今回例に挙げた関数の展開を自分の手で計算し直して慣れてもらいたい。
END





コメント