【微積分】二変数関数の停留点(極大点・極小点・鞍点)②～問題演習～

　下記記事にて、二変数関数の停留点の求め方を解説した。

　今回は付録的な記事になるが、上の記事で扱った例題の類題を解いていく。

問題演習

解説

(1)

　まず、二変数関数\(f(x,y)\)の停留点を求める。

　\(\displaystyle{\frac{\partial f(x,y)}{\partial x}=\frac{\partial f(x,y)}{\partial y}=0}\)を満たす\((x,y)\)の組を求めればよいので、

\begin{gather}
\begin{cases}
\displaystyle{\frac{\partial f(x,y)}{\partial x}=3x^{2}-3y=0} \\ \
\displaystyle{\frac{\partial f(x,y)}{\partial y}=3y^{2}-3x=0}
\end{cases}\tag{1}\label{teiryurenmon1-1}\\
\downarrow\notag\\
\begin{cases}
x^{2}-y=0 \\
y^{2}-x=0
\end{cases}\tag{2}\label{teiryurenmon1-2}
\end{gather}

となる。

　連立方程式(\ref{teiryurenmon1-2})を解くと\((x,y)=(0,0),(1,1)\)となるため、停留点は\((a_{x},a_{y})=(0,0),(1,1)\)となる。

　続いて停留点の種類を判定する。まず、二階の偏導関数を求めると

\begin{align}
&\frac{\partial^{2} f(x,y)}{\partial x^{2}}=6x \tag{3}\label{teiryuxx1} \\
&\frac{\partial^{2} f(x,y)}{\partial x\partial y}=-3 \tag{4}\label{teiryuxy1} \\
&\frac{\partial^{2} f(x,y)}{\partial y^{2}}=6y \tag{5}\label{teiryuyy1}
\end{align}

となるため、ヘッセ行列は(\ref{teiryuxx1})～(\ref{teiryuyy1})より

\begin{align}
\mathsf{H}=\begin{pmatrix}\displaystyle{\frac{\partial^{2} f(x,y)}{\partial x^{2}}}&\displaystyle{\frac{\partial^{2} f(x,y)}{\partial x\partial y}} \\ \\ \displaystyle{\frac{\partial^{2} f(x,y)}{\partial x\partial y}}&\displaystyle{\frac{\partial^{2} f(x,y)}{\partial y^{2}}}\end{pmatrix}=\begin{pmatrix}6x&-3\\-3&6y\end{pmatrix} \tag{6}\label{hesianrei1}
\end{align}

となる。後は(\ref{hesianrei1})に停留点の座標を代入して、ヘッセ行列の固有値を求めればよい。

　\((a_{x},a_{y})=(0,0)\)のとき、ヘッセ行列は(\ref{hesianrei1})より

\begin{align}
\mathsf{H}_{(0,0)}=\begin{pmatrix}0&-3\\-3&0\end{pmatrix}
\end{align}

となる。よって\(\mathsf{H}_{(0,0)}\)の固有値を\(\lambda\)とすると、単位行列を\(\mathsf{I}\)として特性方程式より

\begin{gather}
\text{det}[\mathsf{H}_{(0,0)}-\lambda\mathsf{I}]=0 \notag \\
\begin{vmatrix}-\lambda & -3\\-3&-\lambda\end{vmatrix}=0\notag\\
\lambda^{2}-9=0 \notag \\
\therefore\,\lambda_{1}=3,\lambda_{2}=-3
\end{gather}

となる。2つの固有値の積が負であるため、停留点\((0,0)\)は鞍点である。

　\((a_{x},a_{y})=(-1,-1)\)のとき、ヘッセ行列は(\ref{hesianrei1})より

\begin{align}
\mathsf{H}_{(1,1)}=\begin{pmatrix}6&-3\\-3&6\end{pmatrix}
\end{align}

となる。よって\(\mathsf{H}_{(1,1)}\)の固有値を\(\lambda\)とすると、単位行列を\(\mathsf{I}\)として特性方程式より

\begin{gather}
\text{det}[\mathsf{H}_{(1,1)}-\lambda\mathsf{I}]=0 \notag \\
\begin{vmatrix}6-\lambda & -3\\-3&6-\lambda\end{vmatrix}=0\notag\\
(6-\lambda)^{2}-9=0 \notag \\
\therefore\,\lambda_{1}=3,\lambda_{2}=9
\end{gather}

となる。2つの固有値がともに正であるため、停留点\((1,1)\)は極小点である。

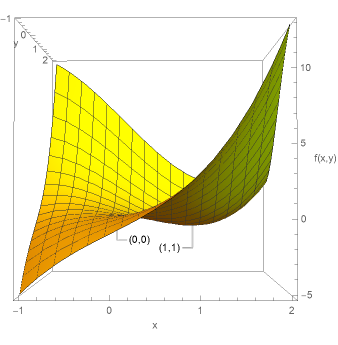
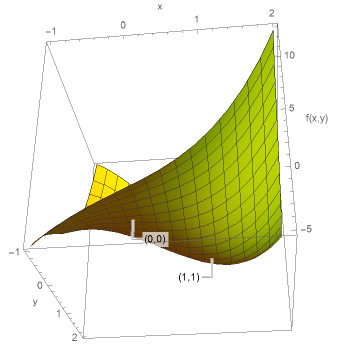
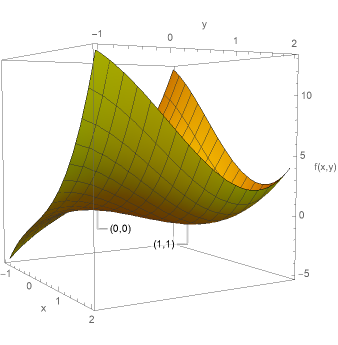
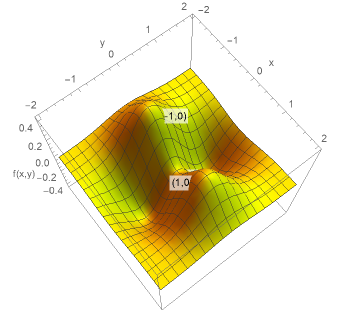
　図1に\(f(x,y)=x^{3}+y^{3}-3xy\)のグラフを示す。実際に\((0,0)\)が鞍点、\((1,1)\)が極小点となっていることがわかると思う。

　

(2)

　まず、二変数関数\(f(x,y)\)の停留点を求める。

　\(\displaystyle{\frac{\partial f(x,y)}{\partial x}=\frac{\partial f(x,y)}{\partial y}=0}\)を満たす\((x,y)\)の組を求めればよいので、

\begin{gather}
\begin{cases}
\displaystyle{\frac{\partial f(x,y)}{\partial x}=2xe^{-x^{2}-y^{2}}-2x(x^{2}-y^{2})e^{-x^{2}-y^{2}}=0} \\ \\
\displaystyle{\frac{\partial f(x,y)}{\partial y}=-2ye^{-x^{2}-y^{2}}-2y(x^{2}-y^{2})e^{-x^{2}-y^{2}}=0}
\end{cases}\tag{7}\label{teiryurenmon2-1}\\
\downarrow\notag\\
\begin{cases}
x(1-x^{2}+y^{2})=0 \\
y(1+x^{2}-y^{2})=0
\end{cases}\tag{8}\label{teiryurenmon2-2}
\end{gather}

となる。

　連立方程式(\ref{teiryurenmon2-2})を解くと\((x,y)=(0,0),(0,\pm 1),(\pm 1,0)\)となるため、停留点は\((a_{x},a_{y})=(0,0),(0,\pm 1),(\pm 1,0)\)となる。

　続いて停留点の種類を判定する。まず、二階の偏導関数を求めると

\begin{align}
&\frac{\partial^{2} f(x,y)}{\partial x^{2}}=-2(2x^{2}-1)(1-x^{2}+y^{2})e^{-x^{2}-y^{2}}-4x^{2}e^{-x^{2}-y^{2}} \tag{9}\label{teiryuxx2} \\
&\frac{\partial^{2} f(x,y)}{\partial x\partial y}=4xy(x^{2}-y^{2})e^{-x^{2}-y^{2}} \tag{10}\label{teiryuxy2} \\
&\frac{\partial^{2} f(x,y)}{\partial y^{2}}=2(2y^{2}-1)(1+x^{2}-y^{2})e^{-x^{2}-y^{2}}+4y^{2}e^{-x^{2}-y^{2}} \tag{11}\label{teiryuyy2}
\end{align}

となるため、ヘッセ行列は(\ref{teiryuxx2})～(\ref{teiryuyy2})より

\begin{align}
\mathsf{H}&=\begin{pmatrix}\displaystyle{\frac{\partial^{2} f(x,y)}{\partial x^{2}}}&\displaystyle{\frac{\partial^{2} f(x,y)}{\partial x\partial y}} \\ \\ \displaystyle{\frac{\partial^{2} f(x,y)}{\partial x\partial y}}&\displaystyle{\frac{\partial^{2} f(x,y)}{\partial y^{2}}}\end{pmatrix} \notag \\
&=e^{-x^{2}-y^{2}}\begin{pmatrix}-2(2x^{2}-1)(1-x^{2}+y^{2})-4x^{2}&4xy(x^{2}-y^{2})\\ \\4xy(x^{2}-y^{2})&2(2y^{2}-1)(1+x^{2}-y^{2})+4y^{2}\end{pmatrix} \tag{12}\label{hesianreimon2}
\end{align}

となる。

　後は(\ref{hesianreimon2})に停留点の座標を代入して、ヘッセ行列の固有値を求めればよい。

　\((a_{x},a_{y})=(0,0)\)のとき、ヘッセ行列は(\ref{hesianreimon2})より

\begin{align}
\mathsf{H}_{(0,0)}=\begin{pmatrix}2&0\\0&-2\end{pmatrix}
\end{align}

となる。よって\(\mathsf{H}_{(0,0)}\)の固有値を\(\lambda\)とすると、単位行列を\(\mathsf{I}\)として特性方程式より

\begin{gather}
\text{det}[\mathsf{H}_{(0,0)}-\lambda\mathsf{I}]=0 \notag \\
\begin{vmatrix}2-\lambda&0\\0&-2-\lambda\end{vmatrix}=0\notag\\
-(2-\lambda)(2+\lambda)=0 \notag \\
\therefore\,\lambda_{1}=2,\lambda_{2}=-2
\end{gather}

となる。2つの固有値の積が負であるため、停留点\((0,0)\)は鞍点である。

　\((a_{x},a_{y})=(0,\pm 1)\)のとき、ヘッセ行列は(\ref{hesianreimon2})より

\begin{align}
\mathsf{H}_{(0,\pm 1)}=\begin{pmatrix}4e^{-1}&0\\0&4e^{-1}\end{pmatrix}
\end{align}

となる。よって\(\mathsf{H}_{(0,\pm 1)}\)の固有値を\(\lambda\)とすると、単位行列を\(\mathsf{I}\)として特性方程式より

\begin{gather}
\text{det}[\mathsf{H}_{(0,\pm 1)}-\lambda\mathsf{I}]=0 \notag \\
\begin{vmatrix}4e^{-1}-\lambda & 0\\0&4e^{-1}-\lambda\end{vmatrix}=0\notag\\
(4e^{-1}-\lambda)^{2}=0 \notag \\
\therefore\,\lambda_{1}=4e^{-1},\lambda_{2}=4e^{-1}
\end{gather}

となる。2つの固有値がともに正であるため、停留点\((0,\pm 1)\)は極小点である。

　\((a_{x},a_{y})=(\pm 1,0)\)のとき、ヘッセ行列は(\ref{hesianreimon2})より

\begin{align}
\mathsf{H}_{(\pm 1,0)}=\begin{pmatrix}-4e^{-1}&0\\0&-4e^{-1}\end{pmatrix}
\end{align}

となる。よって\(\mathsf{H}_{(\pm 1,0)}\)の固有値を\(\lambda\)とすると、単位行列を\(\mathsf{I}\)として特性方程式より

\begin{gather}
\text{det}[\mathsf{H}_{(\pm 1,0)}-\lambda\mathsf{I}]=0 \notag \\
\begin{vmatrix}-4e^{-1}-\lambda & 0\\0&-4e^{-1}-\lambda\end{vmatrix}=0\notag\\
(-4e^{-1}-\lambda)^{2}=0 \notag \\
\therefore\,\lambda_{1}=-4e^{-1},\lambda_{2}=-4e^{-1}
\end{gather}

となる。2つの固有値がともに負であるため、停留点\((\pm 1,0)\)は極大点である。

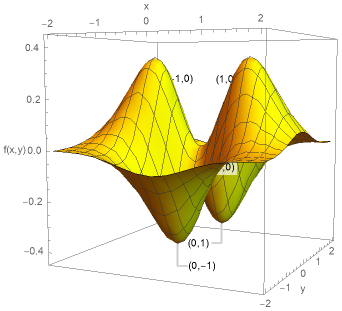
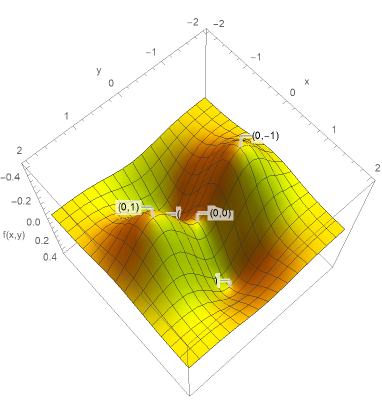
　図2に\(f(x,y)=(x^{2}-y^{2})e^{-x^{2}-y^{2}}\)のグラフを示す。実際に\((0,0)\)が鞍点、\((0,\pm 1)\)が極小点、\((\pm 1,0)\)が極大点となっていることがわかると思う。

終わりに

　大学時代のノートを見返して見つけた問題だったが、案外良い計算練習になった。

　解き方自体は一貫しているので、計算ミスがなければしっかり解ける問題だろう。

　他に良い問題があれば記事にしていこうと思う。

　

　END