これまで、電磁気学の基本方程式であるマクスウェル方程式をそれぞれ詳しく紹介してきた。
ガウスの法則
単磁荷不在の法則
ファラデーの電磁誘導の法則
アンペール・マクスウェルの法則
今回はこれらのマクスウェル方程式を利用して電磁波を導出し、その具体的な性質を調べていく。
真空中の電磁波の導出
ここでマクスウェル方程式をおさらいしておく。
\begin{align}
&\nabla\cdot\vec{E}(\vec{r},t)=\frac{\rho(\vec{r},t)}{\varepsilon_{0}}\qquad\text{(ガウスの法則)} \\
&\nabla\cdot\vec{B}(\vec{r},t)=0 \qquad\text{(単磁荷不在の法則)}\\
&\nabla\times\vec{E}(\vec{r},t)=-\frac{\partial \vec{B}(\vec{r},t)}{\partial t} \qquad\text{(電磁誘導の法則)}\\
&\nabla\times\vec{B}(\vec{r},t)=\mu_{0}\vec{j}+\mu_{0}\varepsilon_{0}\frac{\partial \vec{E}(\vec{r},t)}{\partial t}\qquad\text{(アンペール・マクスウェルの法則)}
\end{align}
上記4つの法則をまとめてマクスウェル方程式と呼ぶ。
特に上記4つは、電場\(\vec{E}(\vec{r},t)\)と磁場\(\vec{B}(\vec{r},t)\)が真空中に発生することを前提としているため、真空中のマクスウェル方程式と呼ばれる。
ここではさらに、電荷と電流が存在しない自由空間を仮定し、その中で電場と磁場がどのように振る舞うのかを調べていく。
電荷と電流が存在しない自由空間では、真空中のマクスウェル方程式は下記のようになる。
\begin{align}
&\nabla\cdot\vec{E}(\vec{r},t)=0 \label{gauss}\tag{1} \\
&\nabla\cdot\vec{B}(\vec{r},t)=0 \label{tanjika}\tag{2}\\
&\nabla\times\vec{E}(\vec{r},t)=-\frac{\partial \vec{B}(\vec{r},t)}{\partial t} \label{faraday}\tag{3}\\
&\nabla\times\vec{B}(\vec{r},t)=\mu_{0}\varepsilon_{0}\frac{\partial \vec{E}(\vec{r},t)}{\partial t} \label{ampmax}\tag{4}
\end{align}
ここで(\ref{faraday})の両辺の回転をとり、ベクトル解析の公式\(\nabla\times(\nabla\times\vec{A})=\nabla(\nabla\cdot\vec{A})-\triangle\vec{A}\)と(\ref{gauss})と(\ref{ampmax})を利用して整理すると
\begin{gather}
\nabla\times\{\nabla\times\vec{E}(\vec{r},t)\}=\nabla\times\left\{-\frac{\partial \vec{B}(\vec{r},t)}{\partial t}\right\}\\
\nabla\{\nabla\cdot\vec{E}(\vec{r},t)\}-\triangle\vec{E}(\vec{r},t)=-\frac{\partial}{\partial t}\nabla\times\vec{B}(\vec{r},t)\\
-\triangle\vec{E}(\vec{r},t)=-\frac{\partial}{\partial t}\mu_{0}\varepsilon_{0}\frac{\partial \vec{E}(\vec{r},t)}{\partial t}\\
\left(\triangle-\mu_{0}\varepsilon_{0}\frac{\partial^{2}}{\partial t^{2}}\right)\vec{E}(\vec{r},t)=0 \label{ehadou}\tag{5}
\end{gather}
となる。
同様にして、(\ref{ampmax})の両辺の回転をとり、ベクトル解析の公式\(\nabla\times(\nabla\times\vec{A})=\nabla(\nabla\cdot\vec{A})-\triangle\vec{A}\)と(\ref{tanjika})と(\ref{faraday})を利用して整理すると
\begin{gather}
\nabla\times\{\nabla\times\vec{B}(\vec{r},t)\}=\nabla\times\left\{\mu_{0}\varepsilon_{0}\frac{\partial \vec{E}(\vec{r},t)}{\partial t}\right\}\\
\nabla\{\nabla\cdot\vec{B}(\vec{r},t)\}-\triangle\vec{B}(\vec{r},t)=\mu_{0}\varepsilon_{0}\frac{\partial}{\partial t}\nabla\times\vec{E}(\vec{r},t)\\
-\triangle\vec{B}(\vec{r},t)=\mu_{0}\varepsilon_{0}\frac{\partial}{\partial t}\left(-\frac{\partial \vec{B}(\vec{r},t)}{\partial t}\right)\\
\left(\triangle-\mu_{0}\varepsilon_{0}\frac{\partial^{2}}{\partial t^{2}}\right)\vec{B}(\vec{r},t)=0 \label{bhadou}\tag{6}
\end{gather}
となる。
(\ref{ehadou})と(\ref{bhadou})は波動方程式の形をしている。
波動方程式とは、ある物理量が波動となって伝搬するときに満たす偏微分方程式であり、伝搬する物理量を\(\vec{u}(\vec{r},t)\)、伝搬速度を\(v\)とすると
\begin{align}
\left(\triangle-\frac{1}{v^{2}}\frac{\partial^{2}}{\partial t^{2}}\right)\vec{u}(\vec{r},t)=0 \label{hadoueq}\tag{7}
\end{align}
と表される。
すなわち自由空間では、電場と磁場は波動となって真空中を伝搬することがわかる。
これが電磁波である。
さらに、それらが伝搬する速度は(\ref{ehadou})、(\ref{bhadou})、(\ref{hadoueq})より
\begin{align}
v=\frac{1}{\sqrt{\mu_{0}\varepsilon_{0}}}=c \label{denjihav}\tag{8}
\end{align}
となり、光速度に一致する。
この結果から、電磁波は真空中では光速度で伝搬することがわかる。
またこの結果からマクスウェルは、光が電磁波の一種であると予想したのである。
平面電磁波
ここから、電磁波の性質を詳しく調べていく。
議論を簡単にするため、電場も磁場も\(x,y\)には依存せず、かつ電場は\(x\)成分のみを持つとする。すなわち、
\begin{align}
&\vec{E}(\vec{r},t)\,\to\,\vec{E}(z,t)=(E_{x}(z,t),0,0)\\
&\vec{B}(\vec{r},t)\,\to\,\vec{B}(z,t)=(B_{x}(z,t),B_{y}(z,t),B_{z}(z,t))
\end{align}
とする。
このとき、\(x,y\)の偏微分はすべて0になるため、自由空間のマクスウェル方程式は下記のようになる。
\begin{align}
&\frac{\partial B_{z}(z,t)}{\partial z}=0 \label{heimentanjika}\tag{9}\\
&\frac{\partial}{\partial z}\left(0,E_{x}(z,t),0\right)=-\frac{\partial}{\partial t}(B_{x}(z,t),B_{y}(z,t),B_{z}(z,t)) \label{heimenfaraday}\tag{10}\\
&\frac{\partial}{\partial z}\left(-B_{y}(z,t),B_{x}(z,t),0\right)=\mu_{0}\varepsilon_{0}\frac{\partial}{\partial t}(E_{x}(z,t),0,0) \label{heimenampmax}\tag{11}
\end{align}
(\ref{heimentanjika})~(\ref{heimenampmax})より、\(B_{y}(z,t),B_{z}(z,t)\)に関する偏微分がすべて0であるため、\(B_{y}(z,t),B_{z}(z,t)\)は定数であることがわかる。
今回はその値を
\begin{align}
B_{y}(z,t)=0,\qquad B_{z}(z,t)=0 \label{ezbz}\tag{12}
\end{align}
とする。
(\ref{ezbz})を利用して(\ref{heimentanjika})~(\ref{heimenampmax})を整理すると、結局
\begin{align}
&\frac{\partial E_{x}(z,t)}{\partial z}=-\frac{\partial B_{y}(z,t)}{\partial t}\label{exby1}\tag{13}\\
&-\frac{\partial B_{y}(z,t)}{\partial z}=\mu_{0}\varepsilon_{0}\frac{\partial E_{x}(z,t)}{\partial t}\label{exby2}\tag{14}
\end{align}
の2式だけが残る。
次に、この(\ref{exby1})と(\ref{exby2})をそれぞれ\(z\)と\(t\)で偏微分する。
\begin{align}
&\frac{\partial^{2} E_{x}(z,t)}{\partial z^{2}}=-\frac{\partial^{2} B_{y}(z,t)}{\partial z\partial t}\label{exby3}\tag{15}\\
&-\frac{\partial^{2} B_{y}(z,t)}{\partial z^{2}}=\mu_{0}\varepsilon_{0}\frac{\partial^{2} E_{x}(z,t)}{\partial z\partial t}\label{exby4}\tag{16}\\
&\frac{\partial^{2} E_{x}(z,t)}{\partial t\partial z}=-\frac{\partial^{2} B_{y}(z,t)}{\partial t^{2}}\label{exby5}\tag{17}\\
&-\frac{\partial^{2} B_{y}(z,t)}{\partial t\partial z}=\mu_{0}\varepsilon_{0}\frac{\partial^{2} E_{x}(z,t)}{\partial t^{2}}\label{exby6}\tag{18}
\end{align}
よって(\ref{exby3})と(\ref{exby6})から
\begin{align}
\left(\frac{\partial^{2}}{\partial z^{2}}-\mu_{0}\varepsilon_{0}\frac{\partial^{2}}{\partial t^{2}}\right)E_{x}(z,t)=0 \label{ezyhadou}\tag{19}
\end{align}
となり、(\ref{exby4})と(\ref{exby5})から
\begin{align}
\left(\frac{\partial^{2}}{\partial z^{2}}-\mu_{0}\varepsilon_{0}\frac{\partial^{2}}{\partial t^{2}}\right)B_{y}(z,t)=0 \label{bzyhadou}\tag{20}
\end{align}
となる。
(\ref{ezyhadou})と(\ref{bzyhadou})は波動方程式であり、(\ref{ezyhadou})に関してはその解として、z軸正の向きに速度\(c=1/\sqrt{\mu_{0}\varepsilon_{0}}\)で伝搬する正弦波
\begin{align}
E_{z}(z,t)=E_{0}\sin k\left(z-ct\right) \label{ezkai}\tag{21}
\end{align}
を採用する。ただし、\(E_{0},k\)は定数である。
ここで(\ref{ezkai})を偏微分方程式(\ref{exby2})に代入して解くと、
\begin{gather}
-\frac{\partial B_{y}(z,t)}{\partial z}=\mu_{0}\varepsilon_{0}\frac{\partial}{\partial t}E_{0}\sin k\left(z-ct\right)\\
\frac{\partial B_{y}(z,t)}{\partial z}=-\mu_{0}\varepsilon_{0}\{-kcE_{0}\cos k(z-ct)\}\\
\frac{\partial B_{y}(z,t)}{\partial z}=\frac{kE_{0}}{c}\cos k(z-ct)\\
B_{y}(z,t)=\frac{E_{0}}{c}\sin k(z-ct)+C \label{byztsakai}\tag{22}
\end{gather}
となる。ただし\(C\)は積分定数であり、今回は\(C=0\)とする。
以上より、自由空間のマクスウェル方程式を満たす電場と磁場として
\begin{align}
\vec{E}(z,t)=E_{0}\sin k(z-ct)(1,0,0) \label{eztkai}\tag{23}\\
\vec{B}(z,t)=\frac{E_{0}}{c}\sin k(z-ct)(0,1,0) \label{bztkai}\tag{24}
\end{align}
が存在することがわかる。
この解は、電磁波の進行方向に垂直な平面上、今回でいうとz軸に垂直な平面上では電場と磁場は一定値をとる。
具体的には\(z=z_{1}\)の平面上では、電場は\(E_{0}\sin k(z_{1}-ct)\)、磁場は\(\displaystyle{\frac{E_{0}}{c}\sin k(z_{1}-ct)}\)であり、\(x,y\)には依存せず、\(z=z_{1}\)の平面上のどこでも電場と磁場は同じ値である。
このような電磁波を平面電磁波と呼ぶ。
また一般に、波面(波動の量が一定値をとる面)が平面である波を平面波と呼ぶ。
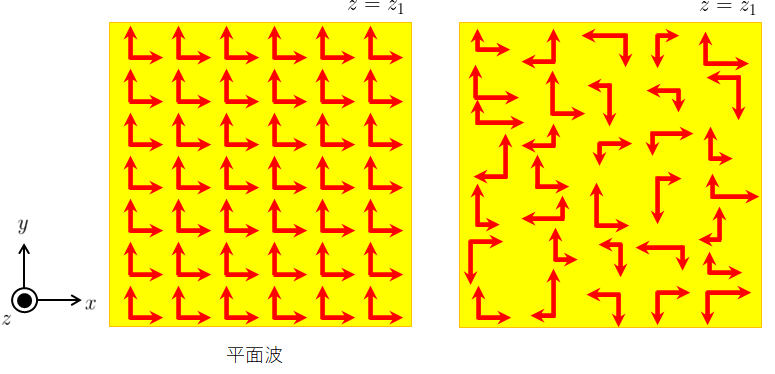
また、平面電磁波では電場と磁場、および電磁波の進行方向は互いに直交し、電磁波の進行方向には電磁波は成分を持たない、すなわち平面電磁波は横波であることがわかる。
終わりに
これで、ひとまず電磁気学でやりたかったことは一通りやった。
もちろん、まだ扱っていないテーマの方がたくさんあるが、切りが良いのでここで電磁気学は一区切りつけ、気が向いたときに扱えなかったテーマを取り上げて記事にしていこうと思う。
個人的には物理に関しては熱力学を勉強しなおしたいと思っているが、どのぐらい時間がかかるか…
END





コメント