【電磁気学】ローレンツ力①～一様磁場中での円運動とらせん運動～

概要
一様磁場のみの系
- 運動の導出
- 荷電粒子の軌跡の導出
終わりに

概要

　電荷\(q\)を有する荷電粒子が、電場\(\vec{E}\)と磁場\(\vec{B}\)が存在する真空中を速度\(\vec{v}\)で運動している。

　このとき、荷電粒子が電場および磁場から受ける力\(\vec{F}\)は次式で表される。

\begin{align}
\vec{F}=q\left\{\vec{E}+\vec{v}\times \vec{B}\right\}\tag{1}\label{ローレンツ力}
\end{align}

　この\(\vec{F}\)をローレンツ力と呼ぶ。

　さらに荷電粒子の質量を\(m\)とし、運動方程式を利用して\(\vec{F}\)と\(\vec{v}\)を変位\(\vec{r}\)の時間微分で表すと

\begin{gather}
m\frac{d^{2}}{dt^{2}}\vec{r}=q\left\{\vec{E}+\frac{d}{dt}\vec{r}\times \vec{B}\right\}\tag{2}\label{ローレンツ力2}
\end{gather}

となる。

一様磁場のみの系

運動の導出

　ローレンツ力の代表例を考える。

　z軸方向に一様磁場\(\vec{B}=(0,0,B)\)が存在する真空中での、質量\(m>0\)、電荷\(q\neq 0\)の荷電粒子の運動を考える。

　初期位置、初速度はそれぞれ\(\vec{r}(0)=(x_{0},y_{0},z_{0}),\vec{v}(0)=(v_{0x},v_{0y},v_{0z})\)とする。

　電場が存在しないため、磁場から受ける力のみを考えればよい。

　(\ref{ローレンツ力2})の右辺に各条件を代入して整理すると

\begin{align}
q\frac{d}{dt}\vec{r}\times \vec{B}&=q\frac{d}{dt}(x,y,z)\times (0,0,B) \notag \\
&=q\frac{d}{dt}(yB,-xB,0) \notag \\
&=qB\frac{d}{dt}(y,-x,0)
\end{align}

となる。

　よって(\ref{ローレンツ力2})は

\begin{gather}
m\frac{d^{2}}{dt^{2}}\vec{r}=qB\frac{d}{dt}(y,-x,0) \notag \\
\frac{d^{2}}{dt^{2}}(x,y,z)=\frac{qB}{m}\frac{d}{dt}(y,-x,0) \tag{3}\label{rei1-1}
\end{gather}

となる。

　ここで速度を

\begin{align}
\vec{v}=(v_{x},v_{y},v_{z})=\frac{d}{dt}(x,y,z)
\end{align}

とすると、(\ref{rei1-1})は

\begin{align}
\frac{d}{dt}(v_{x},v_{y},v_{z})=\frac{qB}{m}(v_{y},-v_{x},0)\tag{4}\label{rei1-2}
\end{align}

となる。

　先にz方向に関して見ていくと、\(dv_{z}/dt=0\)より等速直線運動となるため、初期条件から

\begin{gather}
z(t)=v_{0z}t+z_{0} \tag{5}\label{rei2-2}
\end{gather}

となる。

　x方向とy方向については、(\ref{rei1-2})より

\begin{align}
&\frac{d}{dt}v_{x}=\frac{qB}{m}v_{y} \tag{6}\label{rei1-3}\\
&\frac{d}{dt}v_{y}=-\frac{qB}{m}v_{x} \tag{7}\label{rei1-4}
\end{align}

となる。

　ここで(\ref{rei1-3})を(\ref{rei1-4})に代入して\(v_{x}\)のみの方程式にすると

\begin{gather}
\frac{d}{dt}\left\{\frac{m}{qB}\frac{d}{dt}v_{x}\right\}=-\frac{qB}{m}v_{x} \notag \\
\frac{d^2}{dt^2}v_{x}=-\left(\frac{qB}{m}\right)^{2}v_{x}\tag{8}\label{rei1-5}
\end{gather}

となる。

　(\ref{rei1-5})は単振動の微分方程式であり、一般解は\(C_{1},C_{2}\)を任意定数として

\begin{align}
v_{x}(t)=C_{1}\cos\frac{qB}{m}t+C_{2}\sin\frac{qB}{m}t \tag{9}\label{rei1-6}
\end{align}

となる。

　さらに(\ref{rei1-6})を(\ref{rei1-3})に代入して整理すると

\begin{gather}
\frac{d}{dt}\left(C_{1}\cos\frac{qB}{m}t+C_{2}\sin\frac{qB}{m}t\right)=\frac{qB}{m}v_{y} \notag \\
-\frac{qB}{m}C_{1}\sin\frac{qB}{m}t+\frac{qB}{m}C_{2}\cos\frac{qB}{m}t=\frac{qB}{m}v_{y} \notag \\
v_{y}(t)=-C_{1}\sin\frac{qB}{m}t+C_{2}\cos\frac{qB}{m}t \tag{10}\label{rei1-7}
\end{gather}

となる。

　(\ref{rei1-6})と(\ref{rei1-7})にそれぞれ初期条件\(v_{x}(0)=v_{0x},v_{y}(0)=v_{0y}\)を適用すると、\(C_{1}=v_{0x},C_{2}=v_{0y}\)が得られる。

　よって

\begin{align}
&v_{x}(t)=v_{0x}\cos\frac{qB}{m}t+v_{0y}\sin\frac{qB}{m}t \tag{11}\label{rei2-5}\\
&v_{y}(t)=-v_{0x}\sin\frac{qB}{m}t+v_{0y}\cos\frac{qB}{m}t \tag{12}\label{rei2-6}
\end{align}

となるため、(\ref{rei2-5})と(\ref{rei2-6})の両辺を時間で積分すれば変位が得られ

\begin{align}
&x(t)=\frac{mv_{0x}}{qB}\sin\frac{qB}{m}t-\frac{mv_{0y}}{qB}\cos\frac{qB}{m}t+C_{3} \tag{13}\label{rei2-7}\\
&y(t)=\frac{mv_{0x}}{qB}\cos\frac{qB}{m}t+\frac{mv_{0y}}{qB}\sin\frac{qB}{m}t+C_{4} \tag{14}\label{rei2-8}
\end{align}

となる。ただし\(C_{3},C_{4}\)は積分定数である。

　さらに(\ref{rei2-7})と(\ref{rei2-8})にそれぞれ初期条件\(x(0)=x_{0},y(0)=y_{0}\)を適用すると、\(C_{3}=(mv_{0y}/qB)+x_{0},C_{4}=-(mv_{0x}/qB)+y_{0}\)が得られる。

　これらを(\ref{rei2-7})と(\ref{rei2-8})に代入し、z方向とまとめると

\begin{align}
&x(t)=\frac{mv_{0x}}{qB}\sin\frac{qB}{m}t-\frac{mv_{0y}}{qB}\cos\frac{qB}{m}t+\frac{mv_{0y}}{qB}+x_{0} \tag{15}\label{rei2-9}\\
&y(t)=\frac{mv_{0x}}{qB}\cos\frac{qB}{m}t+\frac{mv_{0y}}{qB}\sin\frac{qB}{m}t-\frac{mv_{0x}}{qB}+y_{0} \tag{16}\label{rei2-10}\\
&z(t)=v_{0z}t+z_{0} \tag{17}\label{rei2-11}
\end{align}

が得られる。

荷電粒子の軌跡の導出

　運動の様子を調べるため、荷電粒子の軌跡を求めてみる。

　\(v_{0xy}=\sqrt{v_{0x}^{2}+v_{0y}^{2}}\)を導入し、\(\cos\phi=v_{0x}/v_{0xy},\sin\phi=v_{0y}/v_{0xy}\)を定義する。

　このとき\(x,y\)はそれぞれ次のように整理できる。

\begin{align}
x(t)&=\frac{mv_{0xy}}{qB}\left(\frac{v_{0x}}{v_{0xy}}\sin\frac{qB}{m}t-\frac{v_{0y}}{v_{0xy}}\cos\frac{qB}{m}t\right)+\frac{mv_{0y}}{qB}+x_{0} \notag \\
&=\frac{mv_{0xy}}{qB}\left(\sin\frac{qB}{m}t\cos\phi-\cos\frac{qB}{m}t\sin\phi\right)+\frac{mv_{0y}}{qB}+x_{0} \notag \\
&=\frac{mv_{0xy}}{qB}\sin\left(\frac{qB}{m}t-\phi\right)+\frac{mv_{0y}}{qB}+x_{0} \tag{18}\label{rei2-12}\\
y(t)&=\frac{mv_{0x}}{qB}\cos\frac{qB}{m}t+\frac{mv_{0y}}{qB}\sin\frac{qB}{m}t-\frac{mv_{0x}}{qB}+y_{0} \notag \\
&=\frac{mv_{0xy}}{qB}\left(\frac{v_{0x}}{v_{0xy}}\cos\frac{qB}{m}t+\frac{v_{0y}}{v_{0xy}}\sin\frac{qB}{m}t\right)-\frac{mv_{0x}}{qB}+y_{0} \notag \\
&=\frac{mv_{0xy}}{qB}\left(\cos\frac{qB}{m}t\cos\phi+\sin\frac{qB}{m}t\sin\phi\right)-\frac{mv_{0x}}{qB}+y_{0} \notag \\
&=\frac{mv_{0xy}}{qB}\cos\left(\frac{qB}{m}t-\phi\right)-\frac{mv_{0x}}{qB}+y_{0} \tag{19}\label{rei2-13}
\end{align}

　さらに(\ref{rei2-12})と(\ref{rei2-13})それぞれについて、最右辺の定数項を最左辺に移項し、両辺を2乗する。

\begin{gather}
x(t)-\left(x_{0}+\frac{mv_{0y}}{qB}\right)=\frac{mv_{0xy}}{qB}\sin\left(\frac{qB}{m}t-\phi\right) \notag \\
\left\{x(t)-\left(x_{0}+\frac{mv_{0y}}{qB}\right)\right\}^{2}=\left(\frac{mv_{0xy}}{qB}\right)^{2}\sin^{2}\left(\frac{qB}{m}t-\phi\right) \tag{20}\label{rei2-14}\\
y(t)-\left(y_{0}-\frac{mv_{0x}}{qB}\right)=\frac{mv_{0xy}}{qB}\cos\left(\frac{qB}{m}t-\phi\right) \notag \\
\left\{y(t)-\left(y_{0}-\frac{mv_{0x}}{qB}\right)\right\}^{2}=\left(\frac{mv_{0xy}}{qB}\right)^{2}\cos^{2}\left(\frac{qB}{m}t-\phi\right)\tag{21}\label{rei2-15}
\end{gather}

　最後に(\ref{rei2-14})と(\ref{rei2-15})の両辺を足し上げれば

\begin{align}
\left\{x(t)-\left(x_{0}+\frac{mv_{0y}}{qB}\right)\right\}^{2}+\left\{y(t)-\left(y_{0}-\frac{mv_{0x}}{qB}\right)\right\}^{2}=\left(\frac{m}{qB}\right)^{2}(v_{0x}^{2}+v_{0y}^{2})
\end{align}

となり、中心\((x_{0}+(mv_{0y}/qB),y_{0}-(mv_{0x}/qB),0)\)、半径\(|m\sqrt{v_{0x}^{2}+v_{0y}^{2}}/qB|\)の円の方程式が得られる。

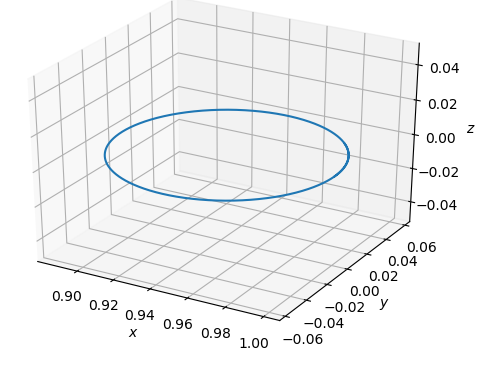
　つまり、荷電粒子はx-y平面内では円運動をする。

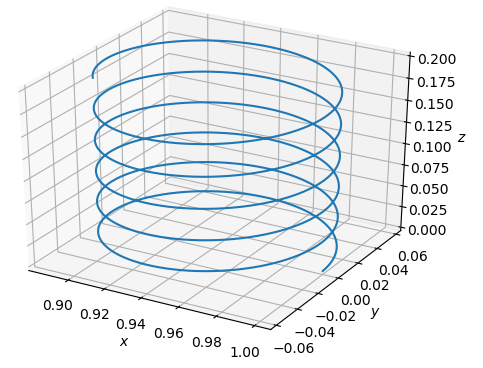
　またz方向に初速度を持っていれば、円運動しながらz方向に等速移動するらせん運動(螺旋運動)となる。

　下図に円運動する場合と螺旋運動する場合の運動例を示す。