にてビオ・サバールの法則を使う問題として、無限長の直線電流、正方形電流が作る磁場を求める問題を見てきた。
今回は、円形電流、ソレノイドが作る磁場を求めていく。
ビオ・サバールの法則
\begin{gather}
\vec{B}(\vec{r})=\frac{\mu_{0}I}{4\pi}\int_{C}\frac{d\vec{r}\,’\times(\vec{r}-\vec{r}\,’)}{|\vec{r}-\vec{r}\,’|^{3}} \label{bio1} \tag{1}
\end{gather}
円形電流が作る磁場
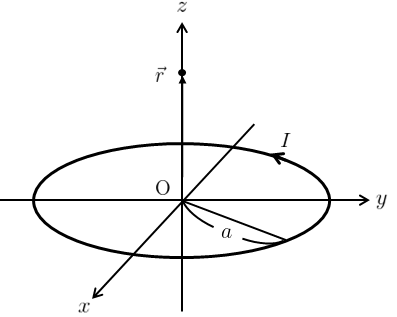
問題3
x-y平面上に半径\(a\)の円形コイルが下図のように置かれ、z軸に対して右ねじの向きに定常電流\(I\)が流れている。
このとき、z軸上の点\(\vec{r}=(0,0,z)\)上に定常電流が作る磁場\(\vec{B}(\vec{r})\)を求めよ。
解説
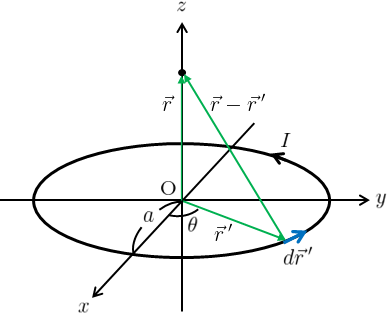
経路\(C\)は円形になるため、極座標表示を採用する。
図2のように設定すると、
\begin{align}
&\vec{r}\,’=(a\cos\theta,a\sin\theta,0)\label{enkeirp}\tag{2}\\
&d\vec{r}\,’=ad\theta(-\sin\theta,\cos\theta,0) \label{enekidr}\tag{3}\\
&\vec{r}-\vec{r}\,’=(-a\cos\theta,-a\sin\theta,z)\label{rmrp}\tag{4}
\end{align}
となる。
よって(\ref{bio1})の積分の中身は
\begin{align}
\frac{d\vec{r}\,’\times(\vec{r}-\vec{r}\,’)}{|\vec{r}-\vec{r}\,’|^{3}}&=\frac{ad\theta(-\sin\theta,\cos\theta,0)\times(-a\cos\theta,-a\sin\theta,z)}{(a^{2}+z^{2})^{\frac{3}{2}}}\\
&=\frac{ad\theta(z\cos\theta,z\sin\theta,a\sin^{2}\theta+a\cos^{2}\theta)}{(a^{2}+z^{2})^{\frac{3}{2}}}\\
&=\frac{ad\theta(z\cos\theta,z\sin\theta,a)}{(a^{2}+z^{2})^{\frac{3}{2}}} \label{ensekinakami}\tag{5}
\end{align}
となるため、これを(\ref{bio1})に代入すると
\begin{align}
\vec{B}(\vec{r})&=\frac{\mu_{0}I}{4\pi}\int_{0}^{2\pi}\frac{ad\theta(z\cos\theta,z\sin\theta,a)}{(a^{2}+z^{2})^{\frac{3}{2}}}\\
&=\frac{\mu_{0}Ia}{4\pi(a^{2}+z^{2})^{\frac{3}{2}}}\left(z\int_{0}^{2\pi}\cos\theta\,d\theta,z\int_{0}^{2\pi}\sin\theta\,d\theta,a\int_{0}^{2\pi}d\theta\right)\\
&=\frac{\mu_{0}Ia}{4\pi(a^{2}+z^{2})^{\frac{3}{2}}}(0,0,2\pi a)\\
&=\frac{\mu_{0}Ia^{2}}{2(a^{2}+z^{2})^{\frac{3}{2}}}(0,0,1) \qquad\therefore\boxed{\vec{B}(\vec{r})=\frac{\mu_{0}Ia^{2}}{2(a^{2}+z^{2})^{\frac{3}{2}}}(0,0,1)}
\end{align}
となり、z成分の磁場しか残らない。
これは円形電流の対称性を考えても納得のいく結果である。
特に\(z=0\)、すなわち円形電流の中心部での磁場は
\begin{align}
\vec{B}(0)=\frac{\mu_{0}I}{2a}(0,0,1) \tag{6}
\end{align}
となり、磁束\(\displaystyle{H=\frac{B}{\mu_{0}}}\)を使えば高校物理で登場する表式\(\displaystyle{H=\frac{I}{2a}}\)が導かれる。
ソレノイドが作る磁場
ビオ・サバールの法則を直接使うわけではないが、前問の結果を利用してソレノイドが作る磁場も求めることができる。
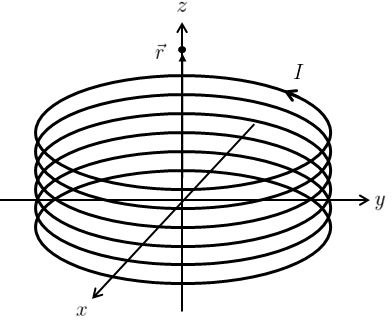
問題4
半径\(a\)、単位長さ当たりの巻き数が\(n\)、中心軸がz軸の無限に長いソレノイドがあり、z軸に対して右ねじの向きに定常電流\(I\)が流れている。
このとき、定常電流がz軸(中心軸)上に作る磁場\(\vec{B}(\vec{r})\)を求めよ。
解説
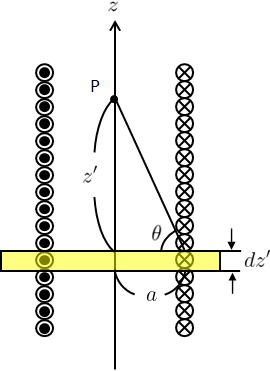
ソレノイドは円形コイルを重ね合わせたものと考えられるため、問題3の結果を利用する。
図4のように、ソレノイドの微小部分\(dz’\)がz軸上の点Pに作る磁場を求め、それを\(z’\)で積分する。
(対称性からz軸上では磁場が一定になると考えられるため、z軸上の1点のみに着目すればよい。)
単位長さ当たりの巻き数が\(n\)であるため、微小部分\(dz’\)に流れる電流は\(nIdz’\)となる。
よって、\(dz’\)がz軸上の点Pに作る磁場\(d\vec{B}\)は問題3の結果から
\begin{align}
d\vec{B}=\frac{\mu_{0}nIa^{2}}{2(a^{2}+z’^{2})^{\frac{3}{2}}}(0,0,1)dz’ \label{dbsore}\tag{7}
\end{align}
となるため、(\ref{dbsore})からz成分を取り出して\(z’\)について積分すればよい。
求める磁場のz成分を\(B_{z}\)とすると
\begin{align}
B_{z}=\int_{-\infty}^{\infty}\frac{\mu_{0}nIa^{2}}{2(a^{2}+z’^{2})^{\frac{3}{2}}}dz’=\frac{\mu_{0}nIa^{2}}{2}\int_{-\infty}^{\infty}\frac{dz’}{(a^{2}+z’^{2})^{\frac{3}{2}}} \label{bzsekibun1}\tag{8}
\end{align}
となる。
ここで、\(z’=a\tan\theta\)と置換すると
\begin{gather}
\frac{dz’}{d\theta}=\frac{a}{\cos^{2}\theta}\\
dz’=\frac{a}{\cos^{2}\theta}d\theta \label{dzdtheta3}\tag{9}
\end{gather}
となるため、(\ref{bzsekibun1})の積分部分に(\ref{dzdtheta3})を代入し、\(\displaystyle{1+\tan^{2}\theta}=\frac{1}{\cos^{2}\theta}\)を利用すると、
\begin{align}
\int_{-\infty}^{\infty}\frac{dz’}{(a^{2}+z’^{2})^{\frac{3}{2}}}&=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{1}{(a^{2}+a^{2}\tan^{2}\theta)^{\frac{3}{2}}}\cdot\frac{a}{\cos^{2}\theta}d\theta\\
&=\frac{1}{a^{2}}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{1}{(1+\tan^{2}\theta)\sqrt{1+\tan^{2}\theta}}\cdot\frac{1}{\cos^{2}\theta}d\theta\\
&=\frac{1}{a^{2}}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{1}{\sqrt{1+\tan^{2}\theta}}d\theta\\
&=\frac{1}{a^{2}}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cos\theta \,d\theta\\
&=\frac{2}{a^{2}} \label{sekibun4}\tag{10}
\end{align}
となる。
よって(\ref{sekibun4})を(\ref{bzsekibun1})に代入すると
\begin{align}
B_{z}=\frac{\mu_{0}nIa^{2}}{2}\cdot\frac{2}{a^{2}}=\mu_{0}nI \tag{11}
\end{align}
となるため、求める磁場は
\begin{align}
\boxed{\vec{B}(\vec{r})=\mu_{0}nI(0,0,1)}
\end{align}
となる。
この結果から、ソレノイドが作る磁場は巻き数と電流に依存し、半径には依存しないことがわかる。
ここで磁束\(\displaystyle{H=\frac{B}{\mu_{0}}}\)を使えば、高校物理で登場する表式\(\displaystyle{H=nI}\)が導かれる。
ここで、ビオ・サバールの法則を使う問題の解説はおしまい。
今まで見てきたように、ビオ・サバールの法則は微小電流が作る磁場を愚直に足し上げていく計算手法をとるため、計算自体がどうしても複雑になりがちである。
しかしいくつかの系では、対称性を利用してアンペールの法則で簡便に磁場を求めることが可能である。
次回からは、そのアンペールの法則を使う問題を扱っていく。
続きはこちら。




コメント