とうとう手を付け始めた。
電磁気学記事全体の方針
基本的に、電磁気学の基礎方程式であるマクスウェル方程式
\begin{align}
&\nabla\cdot\vec{E}(\vec{r},t)=\frac{\rho(\vec{r},t)}{\varepsilon_{0}}\qquad\text{(ガウスの法則)} \\
&\nabla\cdot\vec{B}(\vec{r},t)=0 \qquad\text{(単磁荷不在の法則)}\\
&\nabla\times\vec{E}(\vec{r},t)=-\frac{\partial \vec{B}(\vec{r},t)}{\partial t} \qquad\text{(電磁誘導の法則)}\\
&\nabla\times\vec{B}(\vec{r},t)=\mu_{0}\vec{j}+\mu_{0}\varepsilon_{0}\frac{\partial \vec{E}(\vec{r},t)}{\partial t}\qquad\text{(アンペール・マクスウェルの法則)}
\end{align}
を天下り的に導入して、これら軸に周辺の法則との関係について取り上げ、応用問題の解説を実施する。
ここでは応用問題の解説に重きを置き、各法則を逐一導出することはしない(決して学問に対する正しい態度ではないが)。
最後は真空中の電磁波の導出までもっていって締めようと思う。
果たしてうまくいくか?
まずはガウスの法則から。
ガウスの法則
ガウスの法則(Gaussの法則、Gauss’ Law)は、電場\(\vec{E}(\vec{r},t)\)を発生させる単位体積当たりの電荷量(電荷密度)を\(\rho(\vec{r},t)\)、真空の誘電率を\(\varepsilon_{0}\)として次式で表される。
\begin{align}
\nabla\cdot\vec{E}(\vec{r},t)=\frac{\rho(\vec{r},t)}{\varepsilon_{0}} \label{gaussbibun}\tag{1}
\end{align}
(\ref{gaussbibun})は微分演算子\(\nabla=(\partial/\partial x,\partial/\partial y,\partial/\partial z)\)を用いた表式であり、それを強調してガウスの法則の微分形とよく呼ばれる。
(上で挙げた他の法則についても同様である。)
実際のガウスの法則を利用した問題では、微分形ではなく積分形が使われるのでそれを導出する。
まず、任意の空間\(V\)で(\ref{gaussbibun})の両辺を体積積分する。
\begin{align}
\iiint_{V}\nabla\cdot\vec{E}(\vec{r},t)dV=\iiint_{V}\frac{\rho(\vec{r},t)}{\varepsilon_{0}}dV \label{gaussseki1}\tag{2}
\end{align}
ここで、任意のベクトル関数\(\vec{f}\)について成立する数学の積分定理の1つであるガウスの定理\(\iint_{S}\vec{f}\cdot d\vec{S}=\iiint_{V}\nabla\cdot\vec{f}dV\)を利用すると(\ref{gaussseki1})は
\begin{align}
\iint_{S}\vec{E}(\vec{r},t)\cdot d\vec{S}=\frac{1}{\varepsilon_{0}}\iiint_{V}\rho(\vec{r},t)dV \label{gaussseki2}\tag{3}
\end{align}
と書き直せる。
この(\ref{gaussseki2})がガウスの法則の積分形である。
ただし、\(S\)は体積\(V\)を囲む閉曲面であり、\(d\vec{S}\)は閉曲面\(S\)の法線ベクトル(閉曲面に対して外向きに垂直な単位ベクトル)を\(\vec{n}\)として\(d\vec{S}=\vec{n}dS\)である。
また右辺の\(\iiint_{V}\rho(\vec{r},t)dV\)は電荷密度の体積積分であるため、閉曲面内の全電荷を表していることがわかる。
この全電荷を\(Q\)とすれば
\begin{align}
\iint_{S}\vec{E}(\vec{r},t)\cdot d\vec{S}=\frac{Q}{\varepsilon_{0}}=4\pi k_{0}Q=N \tag{4}
\end{align}
となって、高校物理でお馴染みの電気力線の本数による表式が導かれる。
さらに、電場を閉曲面で面積分すると電気力線の総本数\(N\)になることから、電場は電気力線の面密度と同等であることがわかる。
クーロンの法則との関係
ガウスの法則に含まれる電磁気学の代表法則の1つにクーロンの法則がある。
簡単に復習しておくと、クーロンの法則とは2つの点電荷\(q_{1},q_{2}\)の間にはたらく力の大きさ\(F\)は、点電荷間の距離を\(r\)として
\begin{align}
F=\frac{1}{4\pi\varepsilon_{0}}\frac{|q_{1}q_{2}|}{r^{2}} \label{クーロン} \tag{5}
\end{align}
で表されるというものだ。
このクーロンの法則(\ref{クーロン})を、ガウスの法則と電場の定義式を用いて導出する。
まず、空間上に点電荷\(q_{1}>0\)が位置\(\vec{r}\)に作る電場を\(\vec{E}(\vec{r})\)を求める。
電場\(\vec{E}(\vec{r})\)は点電荷\(q_{1}\)を中心に球対称に発生するため、閉曲面として点電荷\(q_{1}\)を中心とした半径\(r\)の球面を考える。
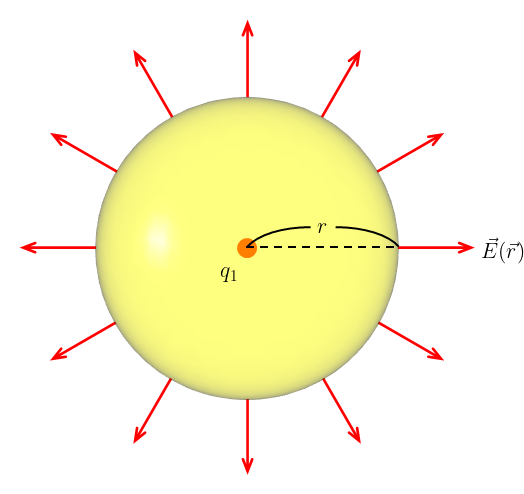
このとき、閉曲面の法線ベクトル\(\vec{n}\)と電場の向きが同じ、すなわち電場の向きを表した単位ベクトル\(\vec{a}\)として\(\vec{n}=\vec{a}\)が成り立つ。
上記と\(\vec{E}(\vec{r})=|\vec{E}(\vec{r})|\vec{a}\)に留意して、閉曲面で(\ref{gaussseki2})の左辺を計算すると
\begin{align}
\iint_{S}\vec{E}(\vec{r})\cdot d\vec{S}&=\iint_{S}|\vec{E}(\vec{r})|\vec{a}\cdot \vec{n}dS\\
&=\iint_{S}|\vec{E}(\vec{r})|dS\\
&=|\vec{E}(\vec{r})|\iint_{S}dS\\
&=4\pi r^{2}|\vec{E}(\vec{r})| \label{gauss左辺} \tag{6}
\end{align}
となる。
次に(\ref{gaussseki2})の右辺だが、\(\iiint_{V}\rho(\vec{r},t)dV\)が閉曲面内での全電荷であり、今回は閉曲面内に点電荷\(q_{1}\)しかないため、
\begin{align}
\frac{1}{\varepsilon_{0}}\iiint_{V}\rho(\vec{r},t)dV=\frac{q_{1}}{\varepsilon_{0}}=\frac{|q_{1}|}{\varepsilon_{0}} \label{gauss右辺} \tag{7}
\end{align}
となる。
よって(\ref{gaussseki2})、(\ref{gauss左辺})、(\ref{gauss右辺})より、
\begin{gather}
4\pi r^{2}|\vec{E}(\vec{r})|=\frac{|q_{1}|}{\varepsilon_{0}} \\
|\vec{E}(\vec{r})|=\frac{1}{4\pi\varepsilon_{0}}\frac{|q_{1}|}{r^{2}} \label{denba1}\tag{8}
\end{gather}
となる。
ここで電場の定義式\(\vec{F}=q\vec{E}\)と(\ref{denba1})を使えば、求める力は
\begin{align}
F=|q_{2}||\vec{E}(\vec{r})|=\frac{1}{4\pi\varepsilon_{0}}\frac{|q_{1}q_{2}|}{r^{2}} \tag{9}
\end{align}
となって\(q_{1}>0\)のときのクーロンの法則が導かれる。
続いて\(q_{1}<0\)のときだが、これは\(\vec{a}\to-\vec{a}, q_{1}=-|q_{1}|\)となるため、この両者のマイナスが相殺されることで結局(\ref{denba1})と同じ形に落ち着く。
典型問題を解いてみる。
ここから、ガウスの法則を利用した典型問題をパターン別に紹介していく。
基本的には、ガウスの法則の典型問題は下記3パターンに区分される。
・電荷分布が球対称な系
・電荷分布が面称な系
・電荷分布が円筒対称な系
まずは各パターンの典型問題の解き方を自分のものにして、それをベースにして他の問題にあたっていけばよいと思う。
では早速、電荷分布が球対称な系を扱う問題から見ていく。
続きはこちら。





コメント