【電磁気学】ローレンツ力②～一様磁場および円筒電場中での荷電粒子の運動①～

　前回

にて一様磁場中でのローレンツ力による荷電粒子の運動を見てきた。

　今回から磁場に加えて、電場も印加した際の電子の振る舞いを調べていく。

　具体的には2回に分けて、2種類の円筒電場を印加する場合を考える。

　片方は解析的に解けるがもう片方は解けないため、運動方程式の導出とシミュレーション結果のみを示すことにする。

　今回は解析的に解ける例を見ていく。

ローレンツ力の復習

　電荷\(q\)を有する荷電粒子が、電場\(\vec{E}\)と磁場\(\vec{B}\)が存在する真空中を速度\(\vec{v}\)で運動している。

　このとき、荷電粒子が電場および磁場から受ける力\(\vec{F}\)は次式で表される。

\begin{align}
\vec{F}=q\left\{\vec{E}+\vec{v}\times \vec{B}\right\}\tag{1}\label{ローレンツ力}
\end{align}

　この\(\vec{F}\)をローレンツ力と呼ぶ。

　

　さらに荷電粒子の質量を\(m\)とし、運動方程式を利用して\(\vec{F}\)と\(\vec{v}\)を変位\(\vec{r}\)の時間微分で表すと

\begin{gather}
m\frac{d^{2}}{dt^{2}}\vec{r}=q\left\{\vec{E}+\frac{d}{dt}\vec{r}\times \vec{B}\right\}\tag{2}\label{ローレンツ力2}
\end{gather}

となる。

一様磁場および距離に応じて大きさが変わる円筒電場の系

系の概要

　z軸方向に一様磁場\(\vec{B}=(0,0,B)\)に加え、電場\(\vec{E}=(-kx,-ky,0)\)が存在する真空中での、質量\(m>0\)、電荷\(q=-e<0\)の電子の運動を考える。

　この電場は動径方向に向きを持ち、中心から遠ざかるに連れてその大きさが大きくなる(下図参照)。

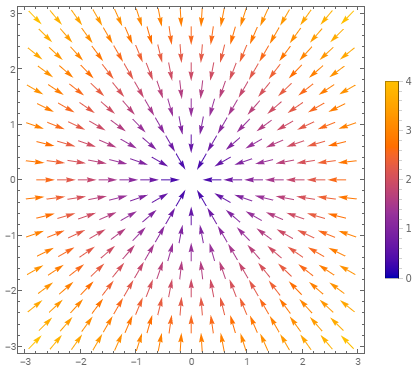
　初期位置と初速度はそれぞれ\(\vec{r}(0)=(x_{0},y_{0},z_{0}),\vec{v}(0)=(v_{0x},v_{0y},v_{0z})\)とする。

運動の導出

　まず(\ref{ローレンツ力2})の右辺に各条件を代入して整理すると

\begin{align}
-e\left\{\vec{E}+\frac{d}{dt}\vec{r}\times \vec{B}\right\}&=-e\left\{\left(-kx,-ky,0\right)+\frac{d}{dt}(x,y,z)\times (0,0,B)\right\} \notag \\
&=-e\left\{\left(-kx,-ky,0\right)+\frac{d}{dt}(yB,-xB,0))\right\} \notag \\
&=-e\left\{-k\left(x,y,0\right)+B\frac{d}{dt}(y,-x,0))\right\}
\end{align}

となる。

　よって(\ref{ローレンツ力2})は

\begin{gather}
m\frac{d^{2}}{dt^{2}}\vec{r}=-e\left\{-k\left(x,y,0\right)+B\frac{d}{dt}(y,-x,0))\right\} \notag \\
\frac{d^{2}}{dt^{2}}(x,y,z)=-\frac{e}{m}\left\{-k\left(x,y,0\right)+B\frac{d}{dt}(y,-x,0))\right\} \tag{3}\label{rei3-1}
\end{gather}

となる。

　よって各成分について抜き出すと
\begin{align}
&\frac{d^{2}}{dt^{2}}x=\frac{ek}{m}x-\frac{eB}{m}\frac{d}{dt}y \tag{4}\label{rei3-7}\\
&\frac{d^{2}}{dt^{2}}y=\frac{ek}{m}y+\frac{eB}{m}\frac{d}{dt}x \tag{5}\label{rei3-8}\\
&\frac{d^{2}}{dt^{2}}z=0 \tag{6}\label{rei3-5}
\end{align}

となる。

　

　z方向に関しては\(dv_{z}/dt=0\)より等速直線運動となるため、初期条件から

\begin{gather}
z(t)=v_{0z}t+z_{0} \tag{7}\label{rei3-6}
\end{gather}

となる。

　

　続いてx方向とy方向を調べる。

　(\ref{rei3-8})の両辺に虚数単位\(i\)をかけたものと(\ref{rei3-7})の両辺を足し合わせて整理すると

\begin{gather}
\frac{d^{2}}{dt^{2}}x+i\frac{d^{2}}{dt^{2}}y=\frac{ek}{m}x-\frac{eB}{m}\frac{d}{dt}y+i\left(\frac{ek}{m}y+\frac{eB}{m}\frac{d}{dt}x\right) \notag \\
\frac{d^{2}}{dt^{2}}(x+iy)=\frac{eB}{m}\frac{d}{dt}(ix-y)+\frac{ek}{m}(x+iy) \notag \\
\frac{d^{2}}{dt^{2}}(x+iy)-\frac{eB}{m}\frac{d}{dt}(ix-y)-\frac{ek}{m}(x+iy)=0 \notag \\
\frac{d^{2}}{dt^{2}}(x+iy)-i\frac{eB}{m}\frac{d}{dt}(x+iy)-\frac{ek}{m}(x+iy)=0 \tag{8}\label{rei3-9}
\end{gather}

　となる。

　よって\(z=x+iy\)とおけば(\ref{rei3-9})は

\begin{align}
\frac{d^{2}}{dt^{2}}z-i\frac{eB}{m}\frac{d}{dt}z-\frac{ek}{m}z=0 \tag{9}\label{rei3-10}
\end{align}

となり、線形斉次の二階の常微分方程式になる。

　\(z=e^{\lambda t}\)とおいて(\ref{rei3-10})に代入して整理すると2次方程式

\begin{align}
\lambda^{2}-i\frac{eB}{m}\lambda-\frac{ek}{m}=0 \tag{10}\label{rei3-11}
\end{align}

が得られるため、これを\((eB/2m)^{2}-(ek/m)\geq 0\)の条件下で解くと

\begin{align}
\lambda=\frac{1}{2}\left(i\frac{eB}{m}\pm\sqrt{-\left(\frac{eB}{m}\right)^{2}+\frac{4ek}{m}}\right)=i\left(\frac{eB}{2m}\pm \sqrt{\left(\frac{eB}{2m}\right)^{2}-\frac{ek}{m}}\right)
\end{align}

が得られる。

　よって

\begin{align}
\omega_{1}=\frac{eB}{2m}+\sqrt{\left(\frac{eB}{2m}\right)^{2}-\frac{ek}{m}},\quad\omega_{2}=\frac{eB}{2m}-\sqrt{\left(\frac{eB}{2m}\right)^{2}-\frac{ek}{m}}
\end{align}

とおくと(\ref{rei3-10})の解として\(z=e^{i\omega_{1}t},e^{i\omega_{2}t}\)の2つが得られたため、(\ref{rei3-10})の一般解は\(C_{1}=a_{1}+ib_{1},C_{2}=a_{2}+ib_{2}\)を複素任意定数として

\begin{align}
z(t)=C_{1}e^{i\omega_{1}t}+C_{2}e^{i\omega_{2}t}\tag{11}\label{rei3-12}
\end{align}

となる。

　ここで\(z=x+iy\)とおいたことを思い出すと、(\ref{rei3-12})は

\begin{align}
&&x(y)+iy(t)=&C_{1}e^{i\omega_{1}t}+C_{2}e^{i\omega_{2}t}\notag \\
&&=&(a_{1}+ib_{1})(\cos\omega_{1}t+i\sin\omega_{1}t)+(a_{2}+ib_{2})(\cos\omega_{2}t+i\sin\omega_{2}t) \notag \\
&&=&a_{1}\cos\omega_{1}t-b_{1}\sin\omega_{1}t+i(a_{1}\sin\omega_{1}t+b_{1}\cos\omega_{1}t) \notag \\
&& &+a_{2}\cos\omega_{2}t-b_{2}\sin\omega_{2}t+i(a_{2}\sin\omega_{2}t+b_{2}\cos\omega_{2}t)\notag \\
&&=&a_{1}\cos\omega_{1}t+a_{2}\cos\omega_{2}t-b_{1}\sin\omega_{1}t-b_{2}\sin\omega_{2}t \notag \\
&& &+i(a_{1}\sin\omega_{1}t+a_{2}\sin\omega_{2}t+b_{1}\cos\omega_{1}t+b_{2}\cos\omega_{2}t)
\end{align}

となるため、(\ref{rei3-7})と(\ref{rei3-8})の一般解は

\begin{align}
&x(t)=a_{1}\cos\omega_{1}t+a_{2}\cos\omega_{2}t-b_{1}\sin\omega_{1}t-b_{2}\sin\omega_{2}t \\
&y(t)=a_{1}\sin\omega_{1}t+a_{2}\sin\omega_{2}t+b_{1}\cos\omega_{1}t+b_{2}\cos\omega_{2}t
\end{align}

となる。

　

　最後に初期条件\(\vec{r}(0)=(x_{0},y_{0},z_{0}),\vec{v}(0)=(v_{0x},v_{0y},v_{0z})\)から\(a_{1},a_{2},b_{1},b_{2}\)を決定する。

　詳細計算は省略するが、結果は

\begin{align}
&a_{1}=\frac{v_{0y}-\omega_{2}x_{0}}{\omega_{1}-\omega_{2}}\tag{12}\label{rei3-38}\\
&a_{2}=-\frac{v_{0y}-\omega_{1}x_{0}}{\omega_{1}-\omega_{2}}\tag{13}\label{rei3-39}\\
&b_{1}=-\frac{v_{0x}+\omega_{2}y_{0}}{\omega_{1}-\omega_{2}}\tag{14}\label{rei3-40}\\
&b_{2}=\frac{v_{0x}+\omega_{1}y_{0}}{\omega_{1}-\omega_{2}}\tag{15}\label{rei3-41}
\end{align}

となる。

　

　まとめると、電子の運動は\((eB/2m)^{2}-(ek/m)\geq 0\)の条件下で下記で表される。

\begin{align}
&x(t)=a_{1}\cos\omega_{1}t+a_{2}\cos\omega_{2}t-b_{1}\sin\omega_{1}t-b_{2}\sin\omega_{2}t \tag{16}\label{rei3-42} \\
&y(t)=a_{1}\sin\omega_{1}t+a_{2}\sin\omega_{2}t+b_{1}\cos\omega_{1}t+b_{2}\cos\omega_{2}t \tag{17}\label{rei3-43}\\
&z(t)=v_{0z}t+z_{0} \tag{18}\label{rei3-44}\\
&\begin{pmatrix}\displaystyle{\omega_{1}=\frac{eB}{2m}+\sqrt{\left(\frac{eB}{2m}\right)^{2}-\frac{ek}{m}}},&\displaystyle{\omega_{2}=\frac{eB}{2m}-\sqrt{\left(\frac{eB}{2m}\right)^{2}-\frac{ek}{m}}}\\
\displaystyle{a_{1}=\frac{v_{0y}-\omega_{2}x_{0}}{\omega_{1}-\omega_{2}}},&\displaystyle{a_{2}=-\frac{v_{0y}-\omega_{1}x_{0}}{\omega_{1}-\omega_{2}}}\\
\displaystyle{b_{1}=-\frac{v_{0x}+\omega_{2}y_{0}}{\omega_{1}-\omega_{2}}},&\displaystyle{b_{2}=\frac{v_{0x}+\omega_{1}y_{0}}{\omega_{1}-\omega_{2}}}
\end{pmatrix}
\end{align}

電子の軌跡の導出

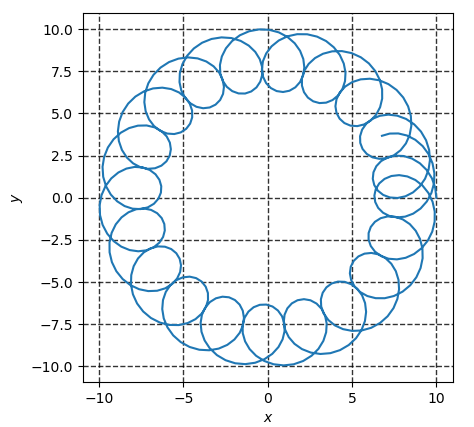
　もう少し具体的に初期値を決め、電子の軌跡を追ってみる。

　初期条件が\(\vec{r}(0)=(x_{0},0,0),\vec{v}(0)=(0,v_{0y},0)\)のとき、各変位は

\begin{align}
&x(t)=a_{1}\cos\omega_{1}t+a_{2}\cos\omega_{2}t \tag{19}\label{rei3-45}\\
&y(t)=a_{1}\sin\omega_{1}t+a_{2}\sin\omega_{2}t \tag{20}\label{rei3-46}\\
&z(t)=0\tag{21}\label{rei3-47}
\end{align}

となる。

　ここで(\ref{rei3-45})と(\ref{rei3-46})の右辺の第1項を左辺に移項し、両辺を2乗して足し上げて整理すると

\begin{align}
\{x(t)-a_{1}\cos\omega_{1}t\}^{2}+\{y(t)-a_{1}\sin\omega_{1}t\}^{2}=a_{2}^{2}
\end{align}

となる。

　すなわち電子はx-y平面上で中心\((a_{1}\cos\omega_{1}t,a_{1}\sin\omega_{1}t)\)、半径\(|a_{2}|\)の円を描く。

　さらにその円の中心もまた、中心\((0,0)\)、半径\(|a_{1}|\)の円周上を動く。

　軌跡の具体例を下図に示す。

終わりに

　最後に円筒電場の系をもう1つ扱って終わりにする。

　

　END

　

　続きはこちら。