前回
にてファラデーの電磁誘導の法則を導入した。
今回からは実際にファラデーの電磁誘導の法則を利用した典型問題をいくつか扱っていく。
前置き
ガウスの法則に引き続き、今回も前置きから。
ファラデーの電磁誘導の法則を使う問題でよく使われる表式は下記の2式だ。
ファラデーの電磁誘導の法則
\begin{gather}
\phi_{\text{em}}=-N\frac{d}{dt}\iint_{S}\vec{B} (\vec{r},t)\cdot d\vec{S} \label{fara1}\tag{1}\\
\phi_{\text{em}}=\int_{C}\{\vec{v}(t)\times\vec{B}(\vec{r},t)\}\cdot d\vec{s} \label{fara2}\tag{2}
\end{gather}
ファラデーの電磁誘導の法則の典型問題で頻出の系は前回述べた通り、大まかに
① 磁場が時間変化する系
② 閉回路が時間変化する系
③ 閉回路以外の導体が運動する系
の3つに大別され、各系において生じる起電力\(\phi_{\text{em}}\)を求めることがゴールになっていることがほとんどである。
基本的にはどの系も(\ref{fara1})の表式で解くことが可能であるが、②と③は表式(\ref{fara2})を用いても解くことができる。
今回は磁場が時間変化する系を見ていく。
この系では(\ref{fara1})を用いる。
磁場が一次的に時間変化する系
まずは最も単純な、磁場の時間変化が一次的な系を見ていく。
問題1
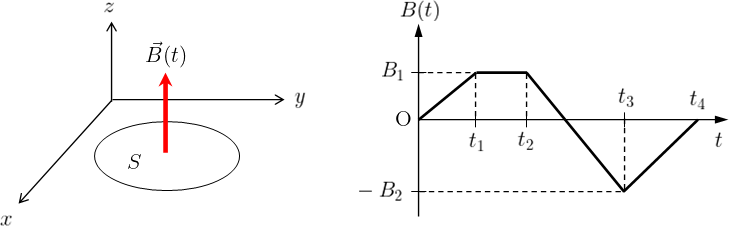
x-y平面上に断面積\(S\)、巻き数\(N\)の円形コイルが置かれている。
さらに、下のグラフのようにz軸方向に時間変化する磁束密度\(\vec{B}(t)=(0,0,B(t))\)が存在する。
このとき、各時間帯においてコイル内で発生する誘導起電力\(\phi_{\text{em}}\)を求めよ。
ただし、磁場は時間変化はするが、位置依存性はなくコイル内で一様であるとする。
解説
方針としては、ファラデーの電磁誘導の法則(\ref{fara1})の右辺を計算して左辺を求めればよい。
(\ref{fara1})の右辺は
\begin{align}
-N\frac{d}{dt}\iint_{S}\vec{B}(t)\cdot d\vec{S}=-N\frac{d}{dt}\{B(t)S\}=-NS\frac{dB(t)}{dt} \label{fara右辺1}\tag{3}
\end{align}
となるため、後は\(B(t)\)を求めて(\ref{fara右辺1})に代入すればよい。
(i) \(0\leq t\leq t_{1}\)のとき、\(B(t)=(B_{1}/t_{1})t\)であるため(\ref{fara右辺1})より
\begin{align}
\phi_{\text{em}}=-NS\frac{d}{dt}\frac{B_{1}}{t_{1}}t=-\frac{B_{1}NS}{t_{1}}\qquad\therefore\boxed{\phi_{\text{em}}=-\frac{B_{1}NS}{t_{1}}}
\end{align}
となる。
(ii) \(t_{1}\leq t\leq t_{2}\)のとき、\(B(t)=B_{1}\)であるため(\ref{fara右辺1})より
\begin{align}
\phi_{\text{em}}=-NS\frac{d}{dt}B_{1}=0\qquad\therefore\boxed{\phi_{\text{em}}=0}
\end{align}
となる。
(iii) \(t_{2}\leq t\leq t_{3}\)のとき、\(\displaystyle{B(t)=-\frac{B_{1}+B_{2}}{t_{3}-t_{2}}t+\frac{B_{1}t_{3}+B_{2}t_{2}}{t_{3}-t_{2}}}\)であるため(\ref{fara右辺1})より
\begin{gather}
\phi_{\text{em}}=-NS\frac{d}{dt}\left\{-\frac{B_{1}+B_{2}}{t_{3}-t_{2}}t+\frac{B_{1}t_{3}+B_{2}t_{2}}{t_{3}-t_{2}}\right\}=\frac{(B_{1}+B_{2})NS}{t_{3}-t_{2}}\\
\therefore\boxed{\phi_{\text{em}}=\frac{(B_{1}+B_{2})NS}{t_{3}-t_{2}}}
\end{gather}
となる。
(iv) \(t_{3}\leq t\leq t_{4}\)のとき、\(\displaystyle{B(t)=\frac{B_{2}}{t_{4}-t_{3}}t-\frac{B_{2}t_{4}}{t_{4}-t_{3}}}\)であるため(\ref{fara右辺1})より
\begin{gather}
\phi_{\text{em}}=-NS\frac{d}{dt}\left\{\frac{B_{2}}{t_{4}-t_{3}}t-\frac{B_{2}t_{4}}{t_{4}-t_{3}}\right\}=-\frac{B_{2}NS}{t_{4}-t_{3}}\\
\therefore\boxed{\phi_{\text{em}}=-\frac{B_{2}NS}{t_{4}-t_{3}}}
\end{gather}
となる。
磁場が周期的に時間変化する系
上の問題は高校物理の範囲で解ける問題だが、次の問題はしっかり磁場の面積分および時間微分を考えなければならない。
問題2
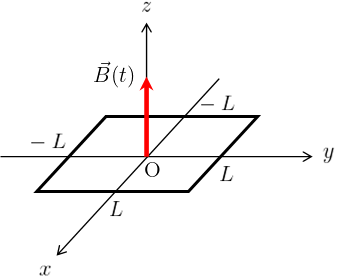
x-y平面上に一辺の長さが\(2L\)、巻き数\(N\)の正方形コイルが下図のように置かれている。
さらに、z軸方向に時間変化する磁束密度
\begin{align}
\vec{B}(t)=(0,0,B\cos(\alpha x)\cos(\beta y)\cos(\omega t))
\end{align}
が存在する。
このとき、次の問いに答えよ。
(a) コイルを貫く磁束\(\Phi(t)\)を求めよ。
(b) コイルに生じる起電力\(\phi_{\text{em}}\)を求めよ。
(c) コイルに抵抗\(R\)を接続したときに生じる電流\(I\)を求めよ。
解説
(a)
磁束密度をコイルの断面\(S\)について面積分すればよい。
今回の系では、面の法線ベクトル\(\vec{n}=(0,0,1)\)であるため、
\begin{align}
\Phi(t)&=\iint_{S}\vec{B}(t)\cdot d\vec{S} \\
&=\iint_{S}(0,0,B\cos(\alpha x)\cos(\beta y)\cos(\omega t))\cdot \vec{n}dS\\
&=\iint_{S}B\cos(\alpha x)\cos(\beta y)\cos(\omega t)\,dS\\
&=\int_{-L}^{L}\int_{-L}^{L}B\cos(\alpha x)\cos(\beta y)\cos(\omega t)\,dxdy\\
&=B\cos(\omega t)\int_{-L}^{L}\cos(\alpha x)\,dx\int_{-L}^{L}\cos(\beta y)\,dy\\
&=B\cos(\omega t)\left[\frac{\sin(\alpha x)}{\alpha}\right]_{-L}^{L}\left[\frac{\sin(\beta y)}{\beta}\right]_{-L}^{L}\\
&=B\cos(\omega t)\cdot\frac{\sin(\alpha L)-\sin(-\alpha L)}{\alpha}\cdot\frac{\sin(\beta L)-\sin(-\beta L)}{\beta}\\
&=B\cos(\omega t)\cdot\frac{2\sin(\alpha L)}{\alpha}\cdot\frac{2\sin(\beta L)}{\beta}\\
&=\frac{4B\sin(\alpha L)\sin(\beta L)\cos(\omega t)}{\alpha\beta}\qquad\therefore\boxed{\Phi(t)=\frac{4B\sin(\alpha L)\sin(\beta L)\cos(\omega t)}{\alpha\beta}}
\end{align}
となる。
(b)
(a)の結果と(\ref{fara1)を利用すると、
\begin{align}
\phi_{\text{em}}&=-N\frac{d}{dt}\frac{4B\sin(\alpha L)\sin(\beta L)\cos(\omega t)}{\alpha\beta}\\
&=-\frac{4BN\sin(\alpha L)\sin(\beta L)}{\alpha\beta}\frac{d}{dt}\cos(\omega t)\\
&=-\frac{4BN\sin(\alpha L)\sin(\beta L)}{\alpha\beta}\cdot\{-\omega\sin(\omega t)\}\\
&=\frac{4BN\omega\sin(\alpha L)\sin(\beta L)\sin(\omega t)}{\alpha\beta} \qquad\therefore\boxed{\phi_{\text{em}}=\frac{4BN\omega\sin(\alpha L)\sin(\beta L)\sin(\omega t)}{\alpha\beta}}
\end{align}
となる。
(c)
(b)の結果とオームの法則を利用すれば、
\begin{align}
I=\frac{\phi_{\text{em}}}{R}=\frac{4BN\omega\sin(\alpha L)\sin(\beta L)\sin(\omega t)}{R\alpha\beta} \qquad\therefore\boxed{I=\frac{4BN\omega\sin(\alpha L)\sin(\beta L)\sin(\omega t)}{R\alpha\beta}}
\end{align}
となる。
磁場が時間変化する系の問題はここでおしまい。
今回は磁場そのものが時間変化するパターンを見てきたが、磁束の時間変化は一様磁場中の閉回路が時間変化することでも生じる。
次は、この閉回路が時間変化する問題を取り上げていく。
続きはこちら。




コメント