【電磁気学】ファラデーの電磁誘導の法則④～例題：閉回路以外の導体が運動する系～

　前回

に引き続き、ファラデーの電磁誘導の法則に関する典型問題を解説する。

　最後となる今回は、閉回路以外の導体が運動する系を扱っていく。

　この系では、下記の2つの表式のどちらを用いても解くことができる。

　本記事では両方の解き方を示すので、解きやすい方を自分で選んで学習すればよい。

一様磁場中で回転する導体円板(単極誘導)

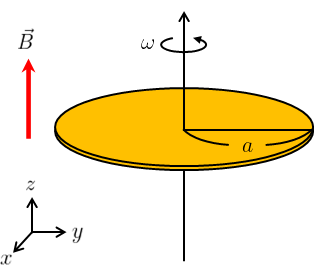
解説

(\ref{fara1})を使う場合

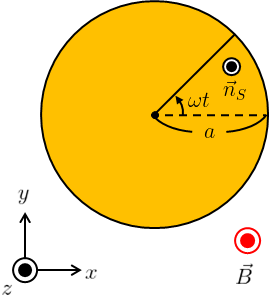
　求めるのは導体円板の中心軸と円周との間に生じる誘導起電力であるため、半径が掃く面積が貫く磁束を時間微分すればよい。

　時間\(t\)の間に半径が掃く面積を\(S(t)\)とすると、

\begin{align}
S(t)=\frac{1}{2}a^{2}\omega t \label{st}\tag{3}
\end{align}

であるため、(\ref{st})を利用して(\ref{fara1})の右辺を計算すると、

\begin{align}
\phi_{\text{em}}&=-\frac{d}{dt}\iint_{S(t)}\vec{B} (\vec{r},t)\cdot d\vec{S(t)} \\
&=-\frac{d}{dt}\iint_{S(t)}\vec{B} (\vec{r},t)\cdot \vec{n}_{S}dS(t) \\
&=-\frac{d}{dt}\iint_{S(t)}(0,0,B)\cdot(0,0,1)dS(t)\\
&=-\frac{d}{dt}B\cdot\frac{1}{2}a^{2}\omega t \\
&=-\frac{1}{2}Ba^{2}\omega \qquad\therefore\boxed{\phi_{\text{em}}=-\frac{1}{2}Ba^{2}\omega}
\end{align}

となる。

　

(\ref{fara2})を使う場合

　求めるのは導体円板の中心軸と円周との間に生じる誘導起電力であるため、半径に生じる誘導電場を求めればよい。

　半径上の位置\(\vec{r}=(r\cos(\omega t),r\sin(\omega t),z)\)における速度\(\vec{v}\)は

\begin{align}
\vec{v}=\frac{\partial}{\partial t}\vec{r}=(-r\omega\sin(\omega t),r\omega\cos(\omega t),0) \label{v}\tag{4}
\end{align}

であるため、(\ref{v})を利用すると誘導電場は

\begin{align}
\vec{v}\times\vec{B}=(-r\omega\sin(\omega t),r\omega\cos(\omega t),0)\times(0,0,B)=(Br\omega\cos(\omega t),Br\omega\sin(\omega t),0) \label{誘導1}\tag{5}
\end{align}

となる。

　さらに上図における扇形の回路の正の方向は、法線ベクトル\(\vec{n}_{S}\)に対して反時計回りであるため、(\ref{fara2})の\(d\vec{s}\)は時間\(t\)後に移動した半径に沿って

\begin{align}
d\vec{s}(t)=(-\cos(\omega t),-\sin(\omega t),0)dr \label{ds}\tag{6}
\end{align}

となる。

　よって(\ref{誘導1})と(\ref{ds})を(\ref{fara2})に代入すると、

\begin{align}
\phi_{\text{em}}&=\int_{C}(\vec{v}\times\vec{B})\cdot d\vec{s}(t) \\
&=\int_{0}^{a}(Br\omega\cos(\omega t),Br\omega\sin(\omega t),0)\cdot(-\cos(\omega t),-\sin(\omega t),0)dr \\
&=\int_{0}^{a}Br\omega\{-\cos^{2}(\omega t)-\sin^{2}(\omega t)\}dr \\
&=-B\omega\int_{0}^{a}rdr \\
&=-B\omega\cdot\frac{1}{2}a^{2}\\
&=-\frac{1}{2}Ba^{2}\omega \qquad\therefore\boxed{\phi_{\text{em}}=-\frac{1}{2}Ba^{2}\omega}
\end{align}

となり、(\ref{fara1})を使った結果と一致する。

　

　今回は一様磁場中で導体円板を回転させたが、一様磁場中でなくとも円柱状の棒磁石を回転させれば同様に誘導起電力が発生する。
　これは単極誘導という名前で知られている現象である。

次回予告

　今回でファラデーの電磁誘導の法則に関する問題解説を一区切りつける。

　次回はマクスウェル方程式のラスト、アンペール・マクスウェルの法則を扱う。

　

　END

　

　※追記
　アンペール・マクスウェルの法則の記事執筆。