【電磁気学】ローレンツ力③～一様磁場および円筒電場中での荷電粒子の運動②～

　前回

にて一様磁場および円筒電場中でのローレンツ力による電子の運動を見てきた。

　今回も前回と似ているが、解析的には電子の運動を記述できない系を扱う。

　解析的には解けないので運動方程式の導出のみで止めるが、今回はデカルト座標系と円筒座標系の2種類の運動方程式を導出してみる。

ローレンツ力の復習

　電荷$q$を有する荷電粒子が、電場$\vec{E}$と磁場$\vec{B}$が存在する真空中を速度$\vec{v}$で運動している。

　このとき、荷電粒子が電場および磁場から受ける力$\vec{F}$は次式で表される。

$$\begin{align} \vec{F}=q\left\{\vec{E}+\vec{v}\times \vec{B}\right\}\tag{1}\label{ローレンツ力} \end{align}$$

　この$\vec{F}$をローレンツ力と呼ぶ。

　

　さらに荷電粒子の質量を$m$とし、運動方程式を利用して$\vec{F}$と$\vec{v}$を変位$\vec{r}$の時間微分で表すと

$$\begin{gather} m\frac{d^{2}}{dt^{2}}\vec{r}=q\left\{\vec{E}+\frac{d}{dt}\vec{r}\times \vec{B}\right\}\tag{2}\label{ローレンツ力2} \end{gather}$$

となる。

一様磁場および大きさ一定の円筒電場の系

系の概要

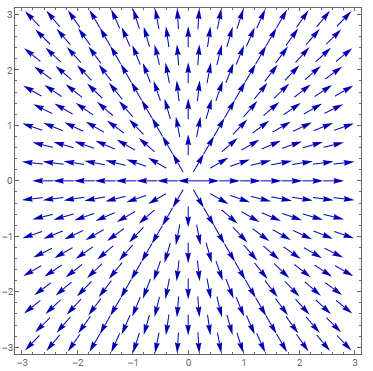
　z軸方向に一様磁場$\vec{B}=(0,0,B)$に加え、電場$\vec{E}=(Ex/\sqrt{x^{2}+y^{2}},Ey/\sqrt{x^{2}+y^{2}},0)$が存在する真空中での、質量$m>0$、電荷$q\neq 0$の荷電粒子の運動を考える。

　この電場は動径方向に向きを持つが、大きさは位置に依存せず一定である(下図参照)。

デカルト座標系での運動方程式の導出

　まず($\ref{ローレンツ力2}$)の右辺に各条件を代入して整理すると

$$\begin{align} q\left\{\vec{E}+\frac{d}{dt}\vec{r}\times \vec{B}\right\}&=q\left\{\left(\frac{Ex}{\sqrt{x^{2}+y^{2}}},\frac{Ey}{\sqrt{x^{2}+y^{2}}},0\right)+\frac{d}{dt}(x,y,z)\times (0,0,B)\right\} \notag \\ &=q\left\{\left(\frac{Ex}{\sqrt{x^{2}+y^{2}}},\frac{Ey}{\sqrt{x^{2}+y^{2}}},0\right)+\frac{d}{dt}(yB,-xB,0))\right\} \notag \\ &=q\left\{E\left(\frac{x}{\sqrt{x^{2}+y^{2}}},\frac{y}{\sqrt{x^{2}+y^{2}}},0\right)+B\frac{d}{dt}(y,-x,0))\right\} \end{align}$$

となる。

　よって($\ref{ローレンツ力2}$)は

$$\begin{gather} m\frac{d^{2}}{dt^{2}}\vec{r}=q\left\{E\left(\frac{x}{\sqrt{x^{2}+y^{2}}},\frac{y}{\sqrt{x^{2}+y^{2}}},0\right)+B\frac{d}{dt}(y,-x,0))\right\} \tag{3}\label{rei3-1} \end{gather}$$

となる。

　よって各成分について抜き出すと

$$\begin{align} &m\frac{d^{2}}{dt^{2}}x=qE\frac{x}{\sqrt{x^{2}+y^{2}}}+qB\frac{d}{dt}y \tag{4}\label{rei3-3}\\ &m\frac{d^{2}}{dt^{2}}y=qE\frac{y}{\sqrt{x^{2}+y^{2}}}-qB\frac{d}{dt}x \tag{5}\label{rei3-4}\\ &m\frac{d^{2}}{dt^{2}}z=0 \tag{6}\label{rei3-5} \end{align}$$

となる。

円筒座標系での運動方程式の導出

　電場が動径方向に広がっているため、円筒座標系で扱うことを考える。

　このとき、$r\geq 0,0\leq\theta<2\pi$として、$x=r\cos\theta,y=r\sin\theta$となる。

　

　導出には、オイラー・ラグランジュ方程式を用いる。

　今回の系におけるラグランジアン$L$は

$$\begin{align} L=\frac{1}{2}m(v_{x}^{2}+v_{y}^{2}+v_{z}^{2})-q(\phi-\vec{v}\cdot \vec{A})\tag{7} \label{rei3-21} \end{align}$$

となる。

　ただし$\phi$は静電ポテンシャル、$\vec{A}$はベクトルポテンシャルであり

$$\begin{align} &\vec{E}=\left(\frac{Ex}{\sqrt{x^{2}+y^{2}}},\frac{Ey}{\sqrt{x^{2}+y^{2}}},0\right)=-\nabla\phi \tag{8}\label{rei3-17}\\ &\vec{B}=(0,0,B)=\nabla\times\vec{A} \tag{9}\label{rei3-18} \end{align}$$

を満たす。

　このとき、

$$\begin{align} &\phi=-E\sqrt{x^{2}+y^{2}}=-Er\tag{10}\label{rei3-19}\\ &\vec{A}=\frac{B}{2}(-y,x,0)=\frac{1}{2}B(-r\sin\theta,r\cos\theta,0)\tag{11}\label{rei3-20} \end{align}$$

となる。

　ここで、速度を円筒座標系で表現する。

$$\begin{align} &v_{x}=\frac{d}{dt}x=\frac{d}{dt}r\cos\theta=\cos\theta\frac{dr}{dt}-r\sin\theta\frac{d\theta}{dt}\tag{12}\label{rei3-13} \\ &v_{y}=\frac{d}{dt}y=\frac{d}{dt}r\sin\theta=\sin\theta\frac{dr}{dt}+r\cos\theta\frac{d\theta}{dt}\tag{13}\label{rei3-14} \\ \end{align}$$

　よって($\ref{rei3-13}$)、($\ref{rei3-14}$)より

$$\begin{align} &&v_{x}^{2}+v_{y}^{2}=&\left(\cos\theta\frac{dr}{dt}-r\sin\theta\frac{d\theta}{dt}\right)^{2}+\left(\sin\theta\frac{dr}{dt}+r\cos\theta\frac{d\theta}{dt}\right)^{2}\notag \\ &&=&\cos^{2}\theta\left(\frac{dr}{dt}\right)^{2}-2r\sin\theta\cos\theta\frac{dr}{dt}\frac{d\theta}{dt}+r^{2}\sin^{2}\theta\left(\frac{d\theta}{dt}\right)^{2}\notag \\ && &+\sin^{2}\theta\left(\frac{dr}{dt}\right)^{2}+2r\sin\theta\cos\theta\frac{dr}{dt}\frac{d\theta}{dt}+r^{2}\cos^{2}\theta\left(\frac{d\theta}{dt}\right)^{2}\notag \\ &&=&\left(\frac{dr}{dt}\right)^{2}+r^{2}\left(\frac{d\theta}{dt}\right)^{2}=v_{r}^{2}+r^{2}v_{\theta}^{2}\tag{14}\label{rei3-15}\\ &&\vec{v}\cdot\vec{A}=&(v_{x},v_{y},v_{z})\cdot \frac{B}{2}(-r\sin\theta,r\cos\theta,0) \notag \\ &&=&\left(\cos\theta\frac{dr}{dt}-r\sin\theta\frac{d\theta}{dt},\sin\theta\frac{dr}{dt}+r\cos\theta\frac{d\theta}{dt},v_{z}\right)\cdot \frac{B}{2}(-r\sin\theta,r\cos\theta,0) \notag \\ &&=&\frac{B}{2}\left(-r\sin\theta\cos\theta\frac{dr}{dt}+r^{2}\sin^{2}\theta\frac{d\theta}{dt}+r\sin\theta\cos\theta\frac{dr}{dt}+r^{2}\cos^{2}\theta\frac{d\theta}{dt}\right) \notag \\ &&=&\frac{Br^{2}}{2}\frac{d\theta}{dt}=\frac{Br^{2}v_{\theta}}{2}\tag{15}\label{rei3-16} \end{align}$$

となる。

　ただし$v_{r}=dr/dt,v_{\theta}=d\theta/dt$とおいた。

　よって($\ref{rei3-19}$)、($\ref{rei3-15}$)、($\ref{rei3-16}$)を($\ref{rei3-21}$)に代入して整理すると

$$\begin{align} L=\frac{1}{2}m(v_{r}^{2}+r^{2}v_{\theta}^{2}+v_{z}^{2})+q\left(Er+\frac{Br^{2}v_{\theta}}{2}\right) \tag{16}\label{rei3-22} \end{align}$$

となり、円筒座標系でのラグランジアンを得られる。

　

　後はこのラグランジアンを円筒座標系でのオイラー・ラグランジュ方程式

$$\begin{align} \frac{d}{dt}\left(\frac{\partial L}{\partial v_{r}}\right)-\frac{\partial L}{\partial r}=0 \tag{17}\label{rei3-23}\\ \frac{d}{dt}\left(\frac{\partial L}{\partial v_{\theta}}\right)-\frac{\partial L}{\partial \theta}=0 \tag{18}\label{rei3-24}\\ \frac{d}{dt}\left(\frac{\partial L}{\partial v_{z}}\right)-\frac{\partial L}{\partial z}=0 \tag{19}\label{rei3-25} \end{align}$$

に代入して運動方程式を求めればよい。

　先にラグランジアンの偏微分を一通り求めておく。

$$\begin{align} \frac{\partial L}{\partial r}&=mrv_{\theta}^{2}+qE+qBrv_{\theta} \tag{20}\label{rei3-26}\\ \frac{\partial L}{\partial \theta}&=0 \tag{21}\label{rei3-27}\\ \frac{\partial L}{\partial z}&=0 \tag{22}\label{rei3-28}\\ \frac{\partial L}{\partial v_{r}}&=mv_{r} \tag{23}\label{rei3-29}\\ \frac{\partial L}{\partial v_{\theta}}&=mr^{2}v_{\theta}+\frac{qBr^{2}}{2} \tag{24}\label{rei3-30}\\ \frac{\partial L}{\partial v_{z}}&=mv_{z}\tag{25}\label{rei3-31} \end{align}$$

　まず$r$について、($\ref{rei3-26}$)と($\ref{rei3-29}$)を($\ref{rei3-23}$)に代入して整理すると

$$\begin{gather} \frac{d}{dt}(mv_{r})-(mrv_{\theta}^{2}+qE+qBrv_{\theta})=0 \notag \\ m\left(\frac{d}{dt}v_{r}-rv_{\theta}^{2}\right)=q(E+Brv_{\theta}) \tag{26}\label{rei3-32} \end{gather}$$

となる。

　次に$\theta$について、($\ref{rei3-27}$)と($\ref{rei3-30}$)を($\ref{rei3-24}$)に代入して整理すると

$$\begin{gather} \frac{d}{dt}\left(mr^{2}v_{\theta}+\frac{qBr^{2}}{2}\right)-0=0 \notag \\ 2mrv_{\theta}\frac{dr}{dt}+mr^{2}\frac{d}{dt}v_{\theta}+qBr\frac{dr}{dt}=0\notag \\ 2mv_{\theta}\frac{dr}{dt}+mr\frac{d}{dt}v_{\theta}+qB\frac{dr}{dt}=0\notag \\ 2mv_{\theta}v_{r}+mr\frac{d}{dt}v_{\theta}+qBv_{r}=0 \notag \\ m\left(r\frac{d}{dt}v_{\theta}+2v_{r}v_{\theta}\right)=-qBv_{r}\tag{27}\label{rei3-33} \end{gather}$$
となる。

　最後に次に$z$について、($\ref{rei3-28}$)と($\ref{rei3-31}$)を($\ref{rei3-25}$)に代入して整理すると

$$\begin{gather} \frac{d}{dt}(mv_{z})-0=0 \notag \\ m\frac{d}{dt}v_{z}=0 \tag{28}\label{rei3-34} \end{gather}$$

となる。

　まとめると、円筒座標系での運動方程式は

$$\begin{align} &m\left(\frac{d}{dt}v_{r}-rv_{\theta}^{2}\right)=q(E+Brv_{\theta}) \tag{29}\label{rei3-35}\\ &m\left(r\frac{d}{dt}v_{\theta}+2v_{r}v_{\theta}\right)=-qBv_{r}\tag{30}\label{rei3-36}\\ &m\frac{d}{dt}v_{z}=0 \tag{31}\label{rei3-37} \end{align}$$

となる。

荷電粒子の軌跡のシミュレーション

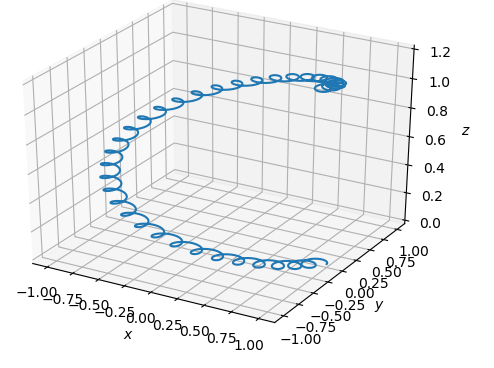
　最後に、上で求めた運動方程式をPythonのSciPyパッケージのodeintモジュールで解いた結果を掲載する。

　荷電粒子の軌跡は、前回見たような二重の円運動となる(図1)。

　z方向に初速度を持っていればらせん運動となる(図2)。

終わりに

　今回の執筆でPythonもかなりいじったので、そこで得られた知見も記事化していこうと思う。

　

　END