前回
にてガウスの法則を導入した。
今回からは実際にガウスの法則を利用した典型問題を扱っていく。
前置き
本題に入る前に、前置き、というか注意事項を2つほど言っておく。
前回の最後に述べた内容を、少し深堀りした内容だ。
出題される問題の電荷分布は大体対称性を持つ。
ガウスの法則
\begin{align}
\iint_{S}\vec{E}(\vec{r},t)\cdot d\vec{S}=\frac{1}{\varepsilon_{0}}\iiint_{V}\rho(\vec{r},t)dV \label{gaussseki2}\tag{1}
\end{align}
は基本的にどの電荷分布でも成立するが、問題集等で扱われている電荷分布は大体は対称性を有している。
電荷分布が対称である場合、閉曲面を上手に設定することで(\ref{gaussseki2})の左辺の計算が楽になるためである。
問題集に掲載されているガウスの法則の応用問題の大半は、電荷分布が
・球対称
・面対称
・円筒対称(線対称を含む)
のいずれかに分類されると考えてよい。
これらの問題の解き方をマスターしてしまえば、後はそのさらなる応用問題でほとんどの問題をカバーできるので解答の敷居はかなり下がるはずだ。
最低限の物理的考察は必要。
どの物理法則でもそうだが、数学の公式とは違ってただ値を代入すれば求めたいものが求まるわけではない。
ガウスの法則の場合は基本的に
・閉曲面の設定
・求める電場の向きの把握
の2つは自分の頭で考えて実施しなければならない。
だが先述の通り、ガウスの法則の利用問題の場合はある程度パターン化されているため、基本問題を押さえてしまえばこの点について困ることはなくなると思う。
球状に分布した電荷が作る電場
今回は上記のパターンの中から、球対称な電荷分布をもつ系の典型問題を扱っていく。
まずは最も典型的な、電荷が球状に分布している系を見ていこう。
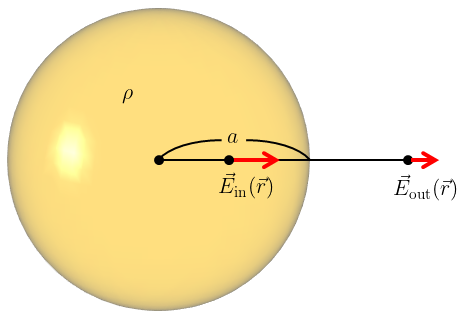
問題1
下図のように半径\(a\)の球の内部に一様な電荷密度\(\rho>0\)で電荷が分布している。
このとき、球の中心を原点として
(a) 球の内部での電場\(\vec{E}_{\text{in}}(\vec{r})\)を求めよ。
(b) 球の外部での電場\(\vec{E}_{\text{out}}(\vec{r})\)を求めよ。
解説
電荷分布が球対称であるため、電場の方向は球の動径方向に一致し、\(\rho>0\)であるため向きは球に対して外向きになる。
よって、閉曲面を電荷が分布する領域の同心球の球面に設定すれば、電場の向きを示す単位ベクトル\(\vec{a}\)と閉曲面の法線ベクトル\(\vec{n}\)が一致する。
具体的には、極座標表示で
\begin{align}
\vec{a}=\vec{n}=(\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta) \label{housen}\tag{2}
\end{align}
となる。
補足(飛ばしても可)
もし\(\rho<0\)の場合は、電場の向きが球に対して内向きになるため、閉曲面の法線ベクトルと方向は一致するが、向きは逆になる。すなわち、
\begin{align}
\vec{a}=-\vec{n}=-(\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta)
\end{align}
となる。
さらに対称性により、球面上の電場の大きさは一定であると考えてよい。
(a)
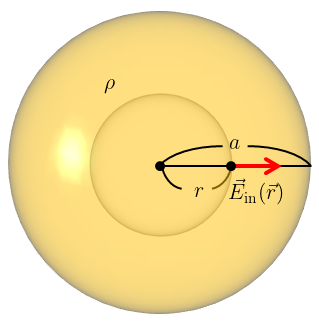
球の内部での電場\(\vec{E}_{\text{in}}(\vec{r})\)は、位置\(\vec{r}\)を含む球面よりも内側の電荷によって形成される。
まずガウスの法則(\ref{gaussseki2})の左辺を計算すると、
\begin{align}
\iint_{S}\vec{E}_{\text{in}}(\vec{r})\cdot d\vec{S}&=\iint_{S}|\vec{E}_{\text{in}}(\vec{r})|\vec{a}\cdot \vec{n}dS \\
&=|\vec{E}_{\text{in}}(\vec{r})|\iint_{S}dS\\
&=4\pi r^{2}|\vec{E}_{\text{in}}(\vec{r})| \label{a1}\tag{3}
\end{align}
となる。
続いて右辺は
\begin{align}
\frac{1}{\varepsilon_{0}}\iiint_{V}\rho dV=\frac{\rho}{\varepsilon_{0}}\iiint_{V} dV=\frac{\rho}{\varepsilon_{0}}\cdot\frac{4}{3}\pi r^{3}=\frac{4\pi\rho r^{3}}{3\varepsilon_{0}} \label{a2}\tag{4}
\end{align}
となる。
よって(\ref{a1})と(\ref{a2})より
\begin{align}
|\vec{E}_{\text{in}}(\vec{r})|=\frac{\rho r}{3\varepsilon_{0}} \tag{5}
\end{align}
となるため、求める電場は(\ref{housen})を利用して
\begin{gather}
\vec{E}_{\text{in}}(\vec{r})=\frac{\rho r}{3\varepsilon_{0}}\vec{a} &\therefore\boxed{\vec{E}_{\text{in}}(\vec{r})=\frac{\rho}{3\varepsilon_{0}}\vec{r}} \tag{6}
\end{gather}
となる。
(b)
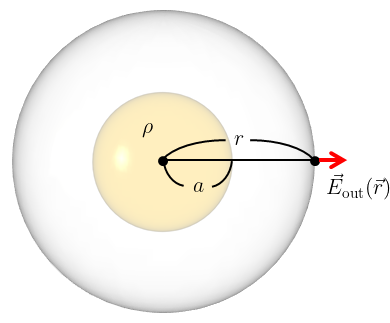
球の外部での電場\(\vec{E}_{\text{out}}(\vec{r})\)は、位置\(\vec{r}\)を含む球面よりも内側の電荷、すなわち系の全電荷によって形成される。
まずガウスの法則(\ref{gaussseki2})の左辺だが、計算自体は(\ref{a1})と同じになり
\begin{align}
\iint_{S}\vec{E}_{\text{out}}(\vec{r})\cdot d\vec{S}=4\pi r^{2}|\vec{E}_{\text{out}}(\vec{r})| \label{b1}\tag{7}
\end{align}
となる。
続いて右辺は
\begin{align}
\frac{1}{\varepsilon_{0}}\iiint_{V}\rho dV&=\frac{\rho}{\varepsilon_{0}}\iiint_{V} dV=\frac{\rho}{\varepsilon_{0}}\cdot\frac{4}{3}\pi a^{3}=\frac{4\pi\rho a^{3}}{3\varepsilon_{0}} \label{b2}\tag{8}
\end{align}
となる。
よって(\ref{b1})と(\ref{b2})より
\begin{align}
|\vec{E}_{\text{out}}(\vec{r})|=\frac{\rho a^{3}}{3\varepsilon_{0}r^{2}} \tag{9}
\end{align}
となるため、求める電場は(\ref{housen})を利用して
\begin{gather}
\vec{E}_{\text{out}}(\vec{r})=\frac{\rho a^{3}}{3\varepsilon_{0}r^{2}}\vec{a} &\therefore\boxed{\vec{E}_{\text{out}}(\vec{r})=\frac{\rho a^{3}}{3\varepsilon_{0}r^{3}}\vec{r}} \tag{10}
\end{gather}
となる。
球面に分布した電荷が作る電場
球対称な電荷分布の類題としてもう1つ、球面(球殻)に一様に電荷が分布している系も見てみる。
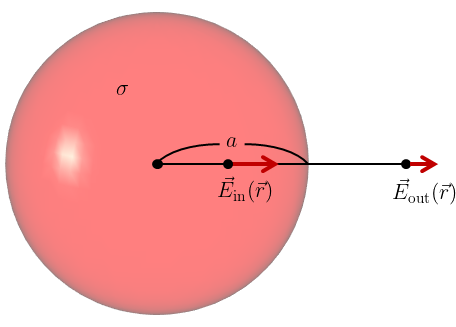
問題2
下図のように半径\(a\)の球の表面に一様な電荷密度\(\sigma>0\)で電荷が分布している。
このとき、球の中心を原点として
(a) 球の内部での電場\(\vec{E}_{\text{in}}(\vec{r})\)を求めよ。
(b) 球の外部での電場\(\vec{E}_{\text{out}}(\vec{r})\)を求めよ。
解説
問題1と同様に考え、表面に電荷を有する球と同心の球を閉曲面に設定すれば、電場と閉曲面の法線ベクトルの向きが一致する。
(a)
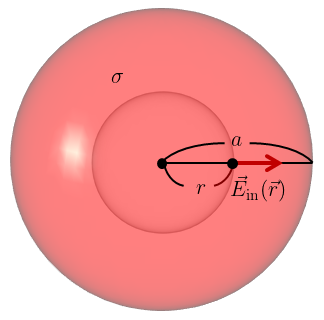
球の内部には電荷がそもそも無い。
よって球の内部に閉曲面を作ってもその内部に電荷が無いため、ガウスの法則(\ref{gaussseki2})の右辺が0になる。
よって電場も0になる。
\begin{align}
\boxed{\vec{E}_{\text{in}}(\vec{r})=\vec{0}} \tag{11}
\end{align}
(b)
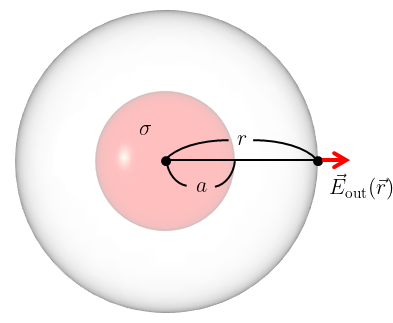
ガウスの法則の左辺の結果は(\ref{b1})に同じ。
右辺は、全電荷が球面に存在することに注意する。
球面を\(S_{\sigma}\)として、体積積分を面積分に書き換えて、
\begin{align}
\frac{1}{\varepsilon_{0}}\iint_{S_{\sigma}}\sigma dS=\frac{1}{\varepsilon_{0}}\cdot 4\pi a^{2}\sigma=\frac{4\pi a^{2}\sigma}{\varepsilon_{0}} \label{b2-2}\tag{12}
\end{align}
となる。
よって(\ref{b1})と(\ref{b2-2})より
\begin{align}
|\vec{E}_{\text{out}}(\vec{r})|=\frac{\sigma a^{2}}{\varepsilon_{0}r^{2}} \tag{13}
\end{align}
となるため、求める電場は(\ref{housen})を利用して
\begin{gather}
\vec{E}_{\text{out}}(\vec{r})=\frac{\sigma a^{2}}{\varepsilon_{0}r^{2}}\vec{a} &\therefore\boxed{\vec{E}_{\text{out}}(\vec{r})=\frac{\sigma a^{2}}{\varepsilon_{0}r^{3}}\vec{r}} \tag{14}
\end{gather}
となる。
電荷分布が球対称な系の問題はここでおしまい。
球対称な系を扱う問題は、教科書の例題として必ずと言っていいほど掲載されており、解法をそのまま暗記しても損はないと思う。
さて次は、電荷分布が面対称な系の問題を取りあげる。
続きはこちら。




コメント