前回
からファラデーの電磁誘導の法則に関する典型問題の解説を開始した。
2回目の今回は、閉回路が時間変化する系を扱っていく。
この系では磁場そのものの時間変化はないが、磁束が貫く面積が時間変化することで回路内の磁束が時間変化し、誘導起電力が発生する。
この系では、下記の2つの表式のどちらを用いても解くことができる。
ファラデーの電磁誘導の法則
\begin{gather}
\phi_{\text{em}}=-N\frac{d}{dt}\iint_{S}\vec{B} (\vec{r},t)\cdot d\vec{S} \label{fara1}\tag{1}\\
\phi_{\text{em}}=\int_{C}\{\vec{v}(t)\times\vec{B}(\vec{r},t)\}\cdot d\vec{s} \label{fara2}\tag{2}
\end{gather}
本記事では両方の解き方を示すので、解きやすい方を自分で選んで学習すればよい。
個人的には(\ref{fara1})を使う方がやりやすいと思う。
一様磁場中の導線上を動く導体棒
まずは磁束が貫く面が一次的に時間変化する問題。
高校物理を履修した人なら見たことがあるであろう関係式「\(V=vB\ell\)」を導出する問題だ。
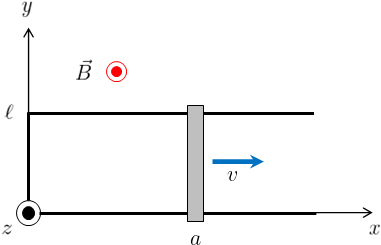
問題1
下図のように、x-y平面上に幅\(\ell\)のU字型の導体レールがあり、その上に導体棒をわたした長方形型の回路がある。
また、z軸正の向きに磁束密度\(\vec{B}=(0,0,B)\)の一様な磁場が存在する。
最初、導体棒は\(x=a\)の位置にいたが、時間\(t=0\)でx軸正の向きに速さ\(v\)でレール上を等速運動し始めた。
このとき、時間\(t=0\)以降の回路に発生する誘導起電力\(\phi_{\text{em}}\)を求めよ。
解説
解き方は、表式(\ref{fara1})を使う方法と表式(\ref{fara2})を使う方法の2種類が存在する。
(i) (\ref{fara1})を使う場合
回路が作る面\(S(t)\)上で、一様磁場\(\vec{B}\)について面積分すればよい。
面\(S(t)\)の法線ベクトル\(\vec{n}_{S}=(0,0,1)\)を利用すれば、(\ref{fara1})の面積分(磁束)の計算は
\begin{align}
\iint_{S(t)}\vec{B}\cdot d\vec{S(t)}=\iint_{S(t)}(0,0,B)\cdot \vec{n}_{S}dS(t) =B\iint_{S(t)}\,dS(t)=B\ell(a+vt) \label{1-1}\tag{3}
\end{align}
となる。
よって(\ref{1-1})を(\ref{fara1})に代入すれば、
\begin{align}
\phi_{\text{em}}=-\frac{d}{dt}B\ell(a+vt)=-vB\ell\qquad\therefore\boxed{\phi_{\text{em}}=-vB\ell}
\end{align}
となる。
(ii) (\ref{fara2})を使う場合
誘導電場は磁場中を動く導体内で発生するため、(\ref{fara2})の線積分は導体棒のみで実行する。
経路\(C\)は回路に沿ってとられ、線積分の向きは回路が作る面の法線ベクトルに対して反時計回りに回る向きになる。
よって今回の系では、経路Cは導体棒に沿ってとられ、線積分の向きは面\(S\)の法線ベクトル\(\vec{n}_{S}=(0,0,1)\)に対して反時計回りに回る向きになるため、導体棒に沿う単位ベクトル(接線ベクトル)を\(\vec{n}_{s}\)として
\begin{align}
d\vec{s}=\vec{n}_{s}dy=(0,-1,0)dy \label{接線1}\tag{4}
\end{align}
となる。
よって誘導電場を求めると、
\begin{align}
\vec{E}=\vec{B}\times\vec{v}=(0,0,B)\times(v,0,0)=(0,vB,0) \label{誘導電場1}\tag{5}
\end{align}
となるため、(\ref{接線1})と(\ref{誘導電場1})を(\ref{fara2})に代入すると、
\begin{align}
\phi_{\text{em}}&=\int_{C}\{\vec{v}\times\vec{B}\}\cdot d\vec{s}\\
&=\int_{0}^{\ell}(0,vB,0)\cdot(0,-1,0)dy\\
&=-vB\int_{0}^{\ell}dy\\
&=-vB\ell \qquad\therefore\boxed{\phi_{\text{em}}=-vB\ell}
\end{align}
となり、(\ref{fara1})を使った結果と一致する。
一様磁場中で回転するコイル
今度は磁束が貫く面が周期的に時間変化する問題だ。
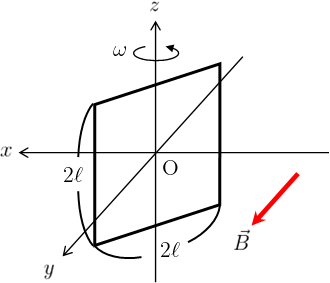
問題2
下図のように、y軸正の向きの一様磁場\(\vec{B}=(0,B,0)\)中に、一辺の長さが\(2\ell\)の正方形コイルが置かれている。
最初この正方形コイルはz-x平面上に、正方形の中心と原点が一致する位置に置かれていたが、\(t=0\)でz軸周りに角速度\(\omega\)で反時計回転し始めた。
このとき、\(t=0\)以降のコイルに発生する誘導起電力\(\phi_{\text{em}}\)を求めよ。
解説
解き方は、表式(\ref{fara1})を使う方法と表式(\ref{fara2})を使う方法の2種類が存在する。
(i) (\ref{fara1})を使う場合
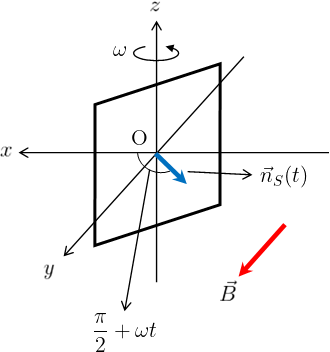
コイルは最初はz-x平面上にあるため、このときの面の法線ベクトル\(\displaystyle{\vec{n}_{S}(0)=\left(\cos\frac{\pi}{2},\sin\frac{\pi}{2},0\right)}\)\(=(0,1,0)\)である。
面が回転し始めると、法線ベクトルはx-y平面上で角速度\(\omega\)で単位円を描く。
よって、時間\(t\)での法線ベクトルは\(\displaystyle{\vec{n}_{S}(t)=\left(\cos\left(\frac{\pi}{2}+\omega t\right),\sin\left(\frac{\pi}{2}+\omega t\right),0\right)}\) \(=(-\sin(\omega t),\cos(\omega t),0)\)となる。
また、法線ベクトルが回転してもコイル面の面積は\(4\ell^{2}\)で変化しないため、(\ref{fara1})の面積分(磁束)の計算は
\begin{align}
\iint_{S(t)}\vec{B}\cdot d\vec{S(t)}&=\iint_{S(t)}(0,B,0)\cdot \vec{n}_{S}(t)dS\\
&=\iint_{S(t)}(0,B,0)\cdot(-\sin(\omega t),\cos(\omega t),0)dS\\
&=B\cos(\omega t)\iint_{S(t)}dS\\
&=4B\ell^{2}\cos(\omega t) \label{2-1}\tag{6}
\end{align}
となる。
(磁束が貫く面の面積は周期的に時間変化していることに注意。)
よって(\ref{2-1})を(\ref{fara1})に代入すれば、
\begin{align}
\phi_{\text{em}}=-\frac{d}{dt}4B\ell^{2}\cos(\omega t)=4B\ell^{2}\omega\sin(\omega t)\qquad\therefore\boxed{\phi_{\text{em}}=4B\ell^{2}\omega\sin(\omega t)}
\end{align}
となる。
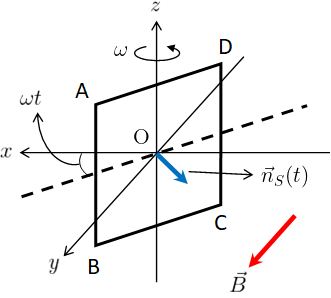
(ii) (\ref{fara2})を使う場合
誘導電場は磁場中を動く導体内で発生するため、今回はコイル全体で(\ref{fara2})の線積分を実行する。
線積分の向きは回路が作る面の法線ベクトルに対して反時計回りに回る向きであり、右図のA→B→C→Dの順になる。
よって全体の線積分は、各辺の線積分に分割して最後に足し上げればよいため、(\ref{fara2})は
\begin{align}
\phi_{\text{em}}&=\int_{C}(\vec{v}\times\vec{B})\cdot d\vec{s} \\
&=\int_{\text{A}\text{B}}(\vec{v}_{\text{AB}}\times\vec{B})\cdot d\vec{s}_{\text{A}\text{B}}+\int_{\text{B}\text{C}}(\vec{v}_{\text{BC}}\times\vec{B})\cdot d\vec{s}_{\text{B}\text{C}}\\
&+\int_{\text{C}\text{D}}(\vec{v}_{\text{CD}}\times\vec{B})\cdot d\vec{s}_{\text{C}\text{D}}+\int_{\text{D}\text{A}}(\vec{v}_{\text{DA}}\times\vec{B})\cdot d\vec{s}_{\text{D}\text{A}} \label{分割和}\tag{7}
\end{align}
となる。
まずは各辺の速度\(\vec{v}\)だが、これは各辺における位置ベクトル\(\vec{r}\)を時間微分すればよい。
円筒座標系を利用すれば、各辺における位置ベクトルは\(-\ell\leq s\leq\ell\)を利用して
\begin{align}
&\vec{r}_{\text{AB}}=(\ell\cos(\omega t),\ell\sin(\omega t),z) \label{rab}\tag{8}\\
&\vec{r}_{\text{BC}}=(s\cos(\omega t),s\sin(\omega t),-\ell) \label{rbc}\tag{9}\\
&\vec{r}_{\text{CD}}=(\ell\cos(\pi+\omega t),\ell\sin(\pi+\omega t),z)=(-\ell\cos(\omega t),-\ell\sin(\omega t),z) \label{rcd}\tag{10}\\
&\vec{r}_{\text{DA}}=(s\cos(\omega t),s\sin(\omega t),\ell) \label{rda}\tag{11}\\
\end{align}
となる。
よって速度は
\begin{align}
&\vec{v}_{\text{AB}}=\frac{\partial}{\partial t}\vec{r}_{\text{AB}}=(-\ell\omega\sin(\omega t),\ell\omega\cos(\omega t),0) \label{vab}\tag{12}\\
&\vec{v}_{\text{BC}}=\frac{\partial}{\partial t}\vec{r}_{\text{BC}}=(-s\omega\sin(\omega t),s\omega\cos(\omega t),0) \label{vbc}\tag{13}\\
&\vec{v}_{\text{CD}}=\frac{\partial}{\partial t}\vec{r}_{\text{CD}}=(\ell\omega\sin(\omega t),-\ell\omega\cos(\omega t),0) \label{vcd}\tag{14}\\
&\vec{v}_{\text{DA}}=\frac{\partial}{\partial t}\vec{r}_{\text{DA}}=(-s\omega\sin(\omega t),s\omega\cos(\omega t),0) \label{vda}\tag{15}\\
\end{align}
となるため、誘導電場は
\begin{align}
&\vec{v}_{\text{AB}}\times{B}=(-\ell\omega\sin(\omega t),\ell\omega\cos(\omega t),0)\times(0,B,0)=(0,0,-B\ell\omega\sin(\omega t)) \label{eab}\tag{16}\\
&\vec{v}_{\text{BC}}\times{B}=(-s\omega\sin(\omega t),s\omega\cos(\omega t),0)\times(0,B,0)=(0,0,-Bs\omega\sin(\omega t)) \label{ebc}\tag{17}\\
&\vec{v}_{\text{CD}}\times{B}=(\ell\omega\sin(\omega t),-\ell\omega\cos(\omega t),0)\times(0,B,0)=(0,0,B\ell\omega\sin(\omega t)) \label{ecd}\tag{18}\\
&\vec{v}_{\text{DA}}\times{B}=(-s\omega\sin(\omega t),s\omega\cos(\omega t),0)\times(0,B,0)=(0,0,-Bs\omega\sin(\omega t)) \label{eda}\tag{19}\\
\end{align}
となる。
続いて\(d\vec{s}\)だが、これは図から
\begin{align}
&d\vec{s}_{\text{AB}}=\vec{n}_{\text{AB}}dz=(0,0,-1)dz \label{dab}\tag{20}\\
&d\vec{s}_{\text{BC}}=\vec{n}_{\text{BC}}ds=(-\cos(\omega t),-\sin(\omega t),0)ds \label{dbc}\tag{21}\\
&d\vec{s}_{\text{CD}}=\vec{n}_{\text{CD}}dz=(0,0,1)dz \label{dcd}\tag{22}\\
&d\vec{s}_{\text{DA}}=\vec{n}_{\text{DA}}ds=(\cos(\omega t),\sin(\omega t),0)ds \label{dda}\tag{23}\\
\end{align}
となる。
よって(\ref{eab})~(\ref{dda})を(\ref{分割和})の各項に代入すると、
\begin{align}
\int_{\text{AB}}(\vec{v}_{\text{AB}}\times\vec{B})\cdot d\vec{s}_{\text{AB}}&=\int_{-\ell}^{\ell}(0,0,-B\ell\omega\sin(\omega t))\cdot (0,0,-1)dz\\
&=\int_{-\ell}^{\ell}B\ell\omega\sin(\omega t)dz=2\ell\cdot B\ell\omega\sin(\omega t)=2B\ell^{2}\omega\sin(\omega t) \label{intab}\tag{24}\\
\int_{\text{BC}}(\vec{v}_{\text{BC}}\times\vec{B})\cdot d\vec{s}_{\text{BC}}&=\int_{-\ell}^{\ell}(0,0,-Bs\omega\sin(\omega t)\cdot (-\cos(\omega t),-\sin(\omega t),0)ds=0\label{intbc}\tag{25}\\
\int_{\text{CD}}(\vec{v}_{\text{CD}}\times\vec{B})\cdot d\vec{s}_{\text{CD}}&=\int_{-\ell}^{\ell}(0,0,B\ell\omega\sin(\omega t))\cdot (0,0,1)dz\\
&=\int_{-\ell}^{\ell}B\ell\omega\sin(\omega t)dz=2\ell\cdot B\ell\omega\sin(\omega t)=2B\ell^{2}\omega\sin(\omega t) \label{intcd}\tag{26}\\
\int_{\text{DA}}(\vec{v}_{\text{DA}}\times\vec{B})\cdot d\vec{s}_{\text{DA}}&=\int_{-\ell}^{\ell}(0,0,-Bs\omega\sin(\omega t))\cdot (\cos(\omega t),\sin(\omega t),0)ds=0\label{intda}\tag{27}
\end{align}
となる。
以上より、(\ref{intab})~(\ref{intda})を(\ref{分割和})に代入すれば
\begin{align}
&\int_{\text{A}\text{B}}(\vec{v}_{\text{AB}}\times\vec{B})\cdot d\vec{s}_{\text{A}\text{B}}+\int_{\text{B}\text{C}}(\vec{v}_{\text{BC}}\times\vec{B})\cdot d\vec{s}_{\text{B}\text{C}}\\
&+\int_{\text{C}\text{D}}(\vec{v}_{\text{CD}}\times\vec{B})\cdot d\vec{s}_{\text{C}\text{D}}+\int_{\text{D}\text{A}}(\vec{v}_{\text{DA}}\times\vec{B})\cdot d\vec{s}_{\text{D}\text{A}} \\
&=2B\ell^{2}\omega\sin(\omega t)+0+2B\ell^{2}\omega\sin(\omega t)+0\\
&=4B\ell^{2}\omega\sin(\omega t) \qquad\therefore\boxed{\phi_{\text{em}}=4B\ell^{2}\omega\sin(\omega t)}
\end{align}
となり、(\ref{fara1})を使った結果と一致する。
閉回路が時間変化する系の問題はここでおしまい。
問題2は座標変換、偏微分、ベクトル解析等の数学がふんだんに使われていて計算練習にもちょうど良く、押さえておいて損はない問題だと思う。
次回でファラデーの電磁誘導の法則を利用する典型問題の解説を一旦しめることにする。
最後は、閉回路以外の導体が静磁場中を運動する系に関する問題を取り上げていく。
続きはこちら。




コメント