【電磁気学】ガウスの法則④～例題：電荷分布が円筒対称な系～

　前回

の電荷分布が面対称な系に引き続き、今回は電荷分布が円筒対称な系を扱う。

　ガウスの法則の典型問題の解説は、今回がラストだ。

円筒状に分布した電荷が作る電場

解説

　無限に長い円筒に電荷が一様に分布しているため、電場の方向は円筒の動径方向に一致し、\(\rho>0\)であるため向きは円筒に対して外向きになる。

　よって閉曲面として、電荷が分布する円筒と同じ軸をもつ半径\(r\)の円筒面に設定すれば、電場の向きを示す単位ベクトル\(\vec{a}\)と閉曲面の側面の法線ベクトル\(\vec{n}\)が一致する。

　具体的には、円筒座標表示で

\begin{align}
\vec{a}=\vec{n}=(\cos\theta,\sin\theta,0) \label{housen}\tag{2}
\end{align}

となる。

　上面と底面については、\(\vec{a}\)と\(\vec{n}\)が垂直で\(\vec{a}\cdot\vec{n}=0\)となるから、ガウスの法則(\ref{gauss})の左辺が0になるので考慮する必要はない。

　閉曲面の円筒の高さは\(h\)として、最後に無限大に飛ばせばよい。

　さらに対称性により、円筒の側面上の電場の大きさは一定であると考えてよい。

　

(a)

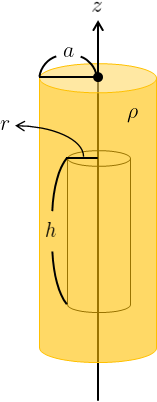
　右図のように、電荷が分布する円筒と同じ軸を有し、位置\(\vec{r}\)を含む円筒状の閉曲面を考える。

　この閉曲面の側面\(S_{\text{side}}\)と、閉曲面内の電荷に対してガウスの法則を適用し、高さ\(h\)を無限大に飛ばせばよい。

　まず、閉曲面内の電荷が作る電場を\(\vec{E’}_{\text{in}}(\vec{r})\)としてガウスの法則(\ref{gauss})の左辺を計算すると、

\begin{align}
\iint_{S}\vec{E’}_{\text{in}}(\vec{r})\cdot d\vec{S}&=\iint_{S_{\text{side}}}|\vec{E’}_{\text{in}}(\vec{r})|\vec{a}\cdot \vec{n}dS \\
&=|\vec{E’}_{\text{in}}(\vec{r})|\iint_{S_{\text{side}}}dS\\
&=2\pi rh|\vec{E’}_{\text{in}}(\vec{r})| \label{a1}\tag{3}
\end{align}

となる。

　続いて右辺は

\begin{align}
\frac{1}{\varepsilon_{0}}\iiint_{V}\rho dV=\frac{\rho}{\varepsilon_{0}}\iiint_{V} dV=\frac{\rho}{\varepsilon_{0}}\cdot \pi r^{2}h=\frac{\pi\rho h r^{2}}{\varepsilon_{0}} \label{a2}\tag{4}
\end{align}

となる。

　よって(\ref{a1})と(\ref{a2})より

\begin{align}
|\vec{E’}_{\text{in}}(\vec{r})|=\frac{\rho r}{2\varepsilon_{0}} \tag{5}
\end{align}

となるため、求める電場は(\ref{housen})を利用して

\begin{gather}
\vec{E}_{\text{in}}(\vec{r})=\lim_{h\to\infty}\frac{\rho r}{2\varepsilon_{0}}\vec{a} &\therefore\boxed{\vec{E}_{\text{in}}(\vec{r})=\frac{\rho}{2\varepsilon_{0}}(r\cos\theta,r\sin\theta,0)} \tag{6}
\end{gather}

となる。

　

(b)

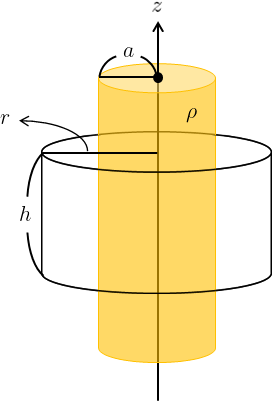
　(a)で設定した閉曲面を、電荷が分布する円柱の外側まで拡張させればよい。

　閉曲面内の電荷が作る電場を\(\vec{E’}_{\text{out}}(\vec{r})\)としてガウスの法則(\ref{gauss})の左辺を計算すると、計算自体は(a)と同じになり、

\begin{align}
\iint_{S}\vec{E’}_{\text{out}}(\vec{r})\cdot d\vec{S}=2\pi rh|\vec{E’}_{\text{out}}(\vec{r})| \label{b1}\tag{7}
\end{align}

となる。

　続いて右辺は

\begin{align}
\frac{1}{\varepsilon_{0}}\iiint_{V}\rho dV&=\frac{\rho}{\varepsilon_{0}}\iiint_{V} dV\\
&=\frac{\rho}{\varepsilon_{0}}\cdot \pi a^{2}h\\
&=\frac{\pi\rho h a^{2}}{\varepsilon_{0}} \label{b2}\tag{8}
\end{align}

となる。

　よって(\ref{b1})と(\ref{b2})より

\begin{align}
|\vec{E’}_{\text{out}}(\vec{r})|=\frac{\rho a^{2}}{2\varepsilon_{0}r} \tag{9}
\end{align}

となるため、求める電場は(\ref{housen})を利用して

\begin{gather}
\vec{E}_{\text{out}}(\vec{r})=\lim_{h\to\infty}\frac{\rho a^{2}}{2\varepsilon_{0}r}\vec{a} &\therefore\boxed{\vec{E}_{\text{out}}(\vec{r})=\frac{\rho a^{2}}{2\varepsilon_{0}r^{2}}(r\cos\theta,r\sin\theta,0)} \tag{10}
\end{gather}

となる。

直線状に分布した電荷が作る電場

　先の円筒状に分布した電荷が作る電場をマスターできれば、直線状に分布した電荷が作る電場も難なく解ける。

解説

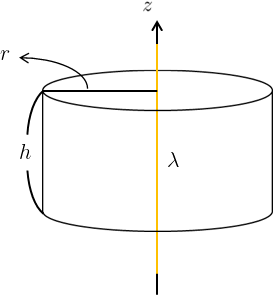
　問題1において、電荷が分布する円筒の半径を限りなく小さくしていった場合に相当する。

　よって、問題1と同じ円筒型の閉曲面を設定すればよい。

　閉曲面内の電荷が作る電場を\(\vec{E’}(\vec{r})\)とすると、ガウスの法則(\ref{gauss})の左辺は問題1と同様の計算で

\begin{align}
\iint_{S}\vec{E’}_{\text{out}}(\vec{r})\cdot d\vec{S}=2\pi rh|\vec{E’}(\vec{r})| \label{2-1}\tag{11}
\end{align}

となる。

　右辺は、電荷が線上に存在することに注意する。
　閉曲面内の線を\(\ell_{\lambda}\)として、体積積分を線積分に書き換えて、

\begin{align}
\frac{1}{\varepsilon_{0}}\int_{\ell_{\lambda}}\lambda d\ell=\frac{1}{\varepsilon_{0}}\cdot h\lambda=\frac{h\lambda}{\varepsilon_{0}} \label{2-2}\tag{12}
\end{align}

となる。

　よって(\ref{2-1})と(\ref{2-2})より

\begin{align}
|\vec{E’}(\vec{r})|=\frac{\lambda}{2\pi \varepsilon_{0}r} \tag{13}
\end{align}

となるため、求める電場は(\ref{housen})を利用して

\begin{gather}
\vec{E}(\vec{r})=\lim_{h\to\infty}\frac{\lambda}{2\pi \varepsilon_{0}r}\vec{a} &\therefore\boxed{\vec{E}(\vec{r})=\frac{\lambda}{2\pi \varepsilon_{0}r^{2}}(r\cos\theta,r\sin\theta,0)} \tag{14}
\end{gather}

となる。

次回予告

　ガウスの法則についてはここで一区切りつける。

　次回からマクスウェル方程式の2つ目、単磁荷不在の法則を取り上げる予定だ。

　

　END

　

　※追記
　マクスウェル方程式2つ目、単磁荷不在の法則の記事執筆。