前回
にてオイラー・ラグランジュ方程式の具体的な使い方を見た。
その後、オイラー・ラグランジュ方程式の練習用に別の問題を作ったのだが、いきなり記事にするにはハードルが高いと思ったためここでワンクッション置くことにした。
今回扱うのは、高校物理でもお馴染みの鉛直ばね振り子である。
問題
鉛直下向きを正とし、ばねが自然長のときの球の位置を\(x=0\)としたとき、球を\(x=L>0\)の位置に移動させてから静かに離した。
球を離した時間を\(t=0\)としたときの、球の変位\(x(t)\)を求めよ。
ただし球は質点とし、空気抵抗は考えなくてよい。
また、重力加速度を\(g\)とする。
解答
球が受ける力は重力とばねによる弾性力であるため、運動方程式は
\begin{align}
m\frac{d^{2}x(t)}{dt^{2}}=-kx(t)+mg \tag{1}\label{undoue}
\end{align}
となる。
上記は線形非斉次の微分方程式であるが、この一般解は「斉次方程式の一般解\(x_{0}(t)\)」と「非斉次方程式の特解\(x_{\text{sp}}(t)\)」の和で記述できる。
斉次方程式はお馴染みの単振動の運動方程式であるため、一般解は
\begin{align}
x_{0}(t)=C\cos(\omega t+\phi) \tag{2}\label{seijiippan}
\end{align}
と書ける。ただし\(\omega=\sqrt{k/m}\)であり。\(C,\phi\)は任意定数である。
特解は(\ref{undoue})を満たす解であれば何でもよい。今回は重力とばねの弾性力が釣り合って球が静止している場合を考える。すなわち、
\begin{align}
0=-kx_{\text{sp}}(t)+mg\quad\therefore\,x_{\text{sp}}(t)=\frac{mg}{k} \tag{3}\label{tokkai}
\end{align}
である。
以上より、(\ref{undoue})の一般解は
\begin{align}
x(t)=C\cos(\omega t+\phi)+\frac{mg}{k} \tag{4}\label{ippan}
\end{align}
となる。
おまけ(読み飛ばしてもよい)
こんな考え方もアリだ。
\(X(t)=x(t)-(mg/k)\)と置いて(\ref{undoue})の右辺を
\begin{align}
-kx(t)+mg=-k\left\{x(t)-\frac{mg}{k}\right\}=-kX(t) \tag{a1}
\end{align}
と変形する。さらに、
\begin{align}
\frac{d^{2}X(t)}{dt^{2}}=\frac{d^{2}}{dt^{2}}\left\{x(t)-\frac{mg}{k}\right\}=\frac{d^{2}x(t)}{dt^{2}} \tag{a2}
\end{align}
であるため、(\ref{undoue})は次式のように変形できる。
\begin{align}
m\frac{d^{2}X(t)}{dt^{2}}=-Kx(t) \tag{a3}\label{a3}
\end{align}
(\ref{a3})はお馴染みの単振動の運動方程式であるため、一般解は
\begin{align}
X(t)=C\cos(\omega t+\phi) \tag{a4}\label{a4}
\end{align}
となる。ただし\(\omega=\sqrt{k/m}\)であり\(C,\phi\)は任意定数である。
よって、そもそも\(X(t)=x(t)-(mg/k)\)であったため、これを(\ref{a4})に代入すれば
\begin{gather}
x(t)-\frac{mg}{k}=C\cos(\omega t+\phi) \\
\therefore\,x(t)=C\cos(\omega t+\phi)+\frac{mg}{k} \tag{a5}
\end{gather}
となり、同じ一般解を求めることができる。
続いて初期条件から任意定数\(C,\phi\)を決定していく。
問題文より\(x(0)=L,\,dx(t)/dt|_{t=0}=0\)であるため、
\begin{align}
&x(0)=C\cos\phi+\frac{mg}{k}=L \\
&\left.\frac{dx(t)}{dt}\right|_{t=0}=-C\omega\sin\phi=0
\end{align}
すなわち
\begin{align}
&C\cos\phi+\frac{mg}{k}=L \tag{5}\label{x0}\\
&C\omega\sin\phi=0 \tag{6}\label{v0}
\end{align}
となる。
\(C=0\)のときは\(L=mg/k\)となり、特解と同様に重力とばねの弾性力が釣り合って球が静止している場合に相当する。
\(C\neq0\)のとき、(\ref{v0})より\(\phi=0\)となる。これを(\ref{x0})に代入すれば、
\begin{align}
C+\frac{mg}{k}=L\quad\therefore\,C=L-\frac{mg}{k} \tag{7}\label{Clast}
\end{align}
となる。
以上より、変位\(x(t)\)は
\begin{align}
x(t)=\left( L-\frac{mg}{k} \right)\cos\left(\sqrt{\frac{k}{m}}\,t\right)+\frac{mg}{k} \tag{8}\label{xtlast}
\end{align}
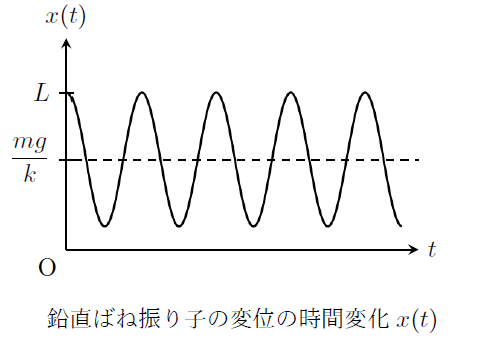
と求められる。この解は、重力とばねの弾性力が釣り合っている状況も含む。
\(L>mg/k\)の場合でグラフを描くと下図のようになり、重力とばねの弾性力が釣り合う位置を中心として単振動することがわかる。
終わりに
次回の内容を言ってしまうと、次回はこの鉛直ばね振り子にもう1つの鉛直ばね振り子を連結させた場合を考えようと思っている。
いきなり球2つの鉛直ばね振り子を扱う前に、1つの場合の運動を見ておいたわけだ。
球1個では単振動するが、2個ではおそらくそこまで単純な運動にはならないだろう。
前に扱った連成振動のように、複雑な運動でもオイラー・ラグランジュ方程式と行列、微分方程式を使って運動をつぶさに記述できる様子を見ていきたい。
END





コメント