高校力学の大きなテーマの1つが衝突である。
と言ってもそこまで難しいものではなく、基本的には2つの式を立てて連立させてしまえば解けてしまうことが多い。
本記事では、ターゲットを外力が存在しない2物体間の衝突に絞り、典型問題を通して問題の種類に応じた解き方を解説する。
問題のパターン
結論を先に述べると、摩擦力などの外力がかかっていない(静止または等速運動している)2物体間の衝突は、運動量保存則、反発係数の式、力学的エネルギー保存の法則の3つの内の2つ以内で記述できる。
さらに問題の種類は、直線上の2物体間の衝突、平面上の2物体間の弾性衝突、片方が動かない(壁や床など)2物体間の衝突の3種類に大別される。
それぞれのパターンで用いる法則、定義をまとめると下記の通りになる。
直線上の2物体間の衝突
運動量保存則
\begin{align}
m_{1}v_{1}+m_{2}v_{2}=m_{1}v’_{1}+m_{2}v’_{2}\tag{1}\label{tyoku2-1}
\end{align}
反発係数の式
\begin{align}
e=-\frac{v’_{1}-v’_{2}}{v_{1}-v_{2}}\tag{2}\label{tyoku2-2}
\end{align}
平面上の2物体間の弾性衝突
運動量保存則
\begin{align}
&m_{1}v_{1x}+m_{2}v_{2x}=m_{1}v’_{1x}+m_{2}v’_{2x}\tag{3}\label{hei2-1}\\
&m_{1}v_{1y}+m_{2}v_{2y}=m_{1}v’_{1y}+m_{2}v’_{2y}\tag{4}\label{hei2-2}
\end{align}
力学的エネルギー保存の法則
\begin{align}
\frac{1}{2}m_{1}v_{1}^{2}+\frac{1}{2}m_{2}v_{2}^{2}=\frac{1}{2}m_{1}{v’_{1}}^{2}+\frac{1}{2}m_{2}{v’_{2}}^{2}\tag{5}\label{hei2-3}
\end{align}
※弾性衝突とは反発係数\(e=1\)となる衝突を指す。

片方が動かない(壁や床など)2物体間の衝突
反発係数の式
\begin{align}
e=-\frac{v’_{y}}{v_{y}}\tag{6}\label{kabe1}
\end{align}
※摩擦力がないため速度の水平成分は変化しない。(\(v_{x}=v’_{x}\))
ただし速度の成分の添え字として、水平成分には\(x\)を、鉛直成分には\(y\)をつけている。(例:\(v_{x},v_{y}\))
問題演習
これらを実感するために、下記の問題を解いてみよう。
問題
滑らかな平面上に3つの小球A,B,Cが水平方向に一直線上に置かれており、水平方向と平行に滑らかな壁が設置されている。質量はA,B,Cそれぞれ\(8.0\,\text{kg},4.0\,\text{kg},1.0\,\text{kg}\)である。
下図のように、AをBに向けて速さ\(1.0\,\text{m/s}\)で打ち出したところ、AはBと非弾性衝突し、その後A,BともにCに向けて等速直線運動を始めた。
その後BはCと弾性衝突し、衝突後Cは壁となす角度が\(\pi/3\)となる向きに等速直線運動を始めた。
さらにその後、Cは壁と非弾性衝突し、衝突後は衝突前と異なる速さで再び等速直線運動を始めた。
ただし、A,B間の反発係数は\(e_{1}=1/2\)、Cと壁との間の反発係数は\(e_{2}=1/\sqrt{3}\)であるとする。

(1) AがBに衝突した後のA,Bそれぞれの速さを求めよ。
(2) BがCに衝突した後のCの速さを求めよ。
(3) Cが壁に衝突した後のCの速さを求めよ。
解説
水平右向き、鉛直上向きを正に取る。
(1)
小球AとBの質量をそれぞれ\(m_{\text{A}},m_{\text{B}}\)、衝突前の速さをそれぞれ\(v_{\text{A}},v_{\text{B}}\)、衝突後の速さをそれぞれ\(v’_{\text{A}},v’_{\text{B}}\)とする。
AとBの衝突は「直線上の2物体間の衝突」であるため運動量保存則(\ref{tyoku2-1})と反発係数の式(\ref{tyoku2-2})を利用する。
まず(\ref{tyoku2-1})より
\begin{gather}
m_{\text{A}}v_{\text{A}}+m_{\text{B}}v_{\text{B}}=m_{\text{A}}v’_{\text{A}}+m_{\text{B}}v’_{\text{B}}\\
8.0\,\text{kg}\times 1.0\,\text{m/s}+4.0\,\text{kg}\times 0\,\text{m/s}=8.0\,\text{kg}\times v’_{\text{A}}+4.0\,\text{kg}\times v’_{\text{B}}\\
8.0\,\text{m/s}=8.0v’_{\text{A}}+4.0v’_{\text{B}}\\
2.0\,\text{m/s}=2.0v’_{\text{A}}+v’_{\text{B}} \label{1-1}\tag{7}
\end{gather}
となる。
続いて(\ref{tyoku2-2})より
\begin{gather}
e_{1}=-\frac{v’_{\text{A}}-v’_{\text{B}}}{v_{\text{A}}-v_{\text{B}}}\\
\frac{1}{2}=-\frac{v’_{\text{A}}-v’_{\text{B}}}{1.0\,\text{m/s}-0\,\text{m/s}}\\
1\,\text{m/s}=-2(v’_{\text{A}}-v’_{\text{B}})\label{1-2}\tag{8}
\end{gather}
となる。
よって(\ref{1-1})と(\ref{1-2})より、求める速さはそれぞれ\(\boxed{v’_{\text{A}}=0.5\,\text{m/s},\, v’_{\text{B}}=1.0\,\text{m/s}}\)となる。
(2)
小球BとCの質量をそれぞれ\(m_{\text{B}},m_{\text{C}}\)とし、衝突前の速さをそれぞれ\(v_{\text{B}},v_{\text{C}}\)、衝突後の速さをそれぞれ\(v’_{\text{B}},v’_{\text{C}}\)とする。
また、衝突後の小球Bと小球Cの進行方向と水平方向がなす角度をそれぞれ\(\theta_{\text{B}},\theta_{\text{C}}\)とする(右図)。
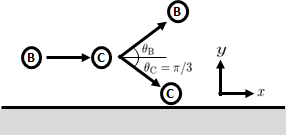
さらに、両者の衝突前の水平方向の速さを\(v_{\text{B}x},v_{\text{C}x}\)、衝突前の鉛直方向の速さを\(v_{\text{B}y},v_{\text{C}y}\)、両者の衝突後の水平方向の速さを\(v’_{\text{B}x},v’_{\text{C}x}\)、衝突後の鉛直方向の速さを\(v’_{\text{B}y},v’_{\text{C}y}\)とする。
BとCの衝突は「平面上の2物体間の弾性衝突」であるため運動量保存則(\ref{hei2-1}),(\ref{hei2-2})と力学的エネルギー保存の法則(\ref{hei2-3})を利用する。
まず(\ref{hei2-1})より
\begin{gather}
m_{\text{B}}v_{\text{B}x}+m_{\text{C}}v_{\text{C}x}=m_{\text{B}}v’_{\text{B}x}+m_{\text{C}}v’_{\text{C}x}\\
4.0\,\text{kg}\times 1.0\,\text{m/s}+1.0\,\text{kg}\times 0\,\text{m/s}=4.0\,\text{kg}\times v’_{\text{B}}\cos\theta_{\text{B}}+1.0\,\text{kg}\times v’_{\text{C}}\cos\theta_{\text{C}}\\
4.0\,\text{m/s}=4.0v’_{\text{B}}\cos\theta_{\text{B}}+v’_{\text{C}}\cos\frac{\pi}{3}\\
4.0\,\text{m/s}=4.0v’_{\text{B}}\cos\theta_{\text{B}}+\frac{1}{2}v’_{\text{C}} \\
8.0\,\text{m/s}=8.0v’_{\text{B}}\cos\theta_{\text{B}}+v’_{\text{C}}\label{2-1}\tag{9}
\end{gather}
となる。
続いて(\ref{hei2-2})より
\begin{gather}
m_{\text{B}}v_{\text{B}y}+m_{\text{C}}v_{\text{C}y}=m_{\text{B}}v’_{\text{B}y}-m_{\text{C}}v’_{\text{C}y}\\
4.0\,\text{kg}\times 0\,\text{m/s}+1.0\,\text{kg}\times 0\,\text{m/s}=4.0\,\text{kg}\times v’_{\text{B}}\sin\theta_{\text{B}}-1.0\,\text{kg}\times v’_{\text{C}}\sin\theta_{\text{C}}\\
0\,\text{m/s}=4.0v’_{\text{B}}\sin\theta_{\text{B}}-v’_{\text{C}}\sin\frac{\pi}{3} \\
0\,\text{m/s}=4.0v’_{\text{B}}\sin\theta_{\text{B}}-\frac{\sqrt{3}}{2}v’_{\text{C}}\\
0\,\text{m/s}=8.0v’_{\text{B}}\sin\theta_{\text{B}}-\sqrt{3}\,v’_{\text{C}}\label{2-2}\tag{10}
\end{gather}
となる。
さらに(\ref{hei2-3})より
\begin{gather}
\frac{1}{2}m_{\text{B}}v_{\text{B}}^{2}+\frac{1}{2}m_{\text{C}}v_{\text{C}}^{2}=\frac{1}{2}m_{\text{B}}{v’_{\text{B}}}^{2}+\frac{1}{2}m_{\text{C}}{v’_{\text{C}}}^{2}\\
4.0\,\text{kg}\times 1.0\,\text{m}^{2}/\text{s}^{2}+1.0\,\text{kg}\times 0\,\text{m}^{2}/\text{s}^{2}=4.0\,\text{kg}\times {v’_{\text{B}}}^{2}+1.0\,\text{kg}\times{v’_{\text{C}}}^{2}\\
4.0\,\text{m}^{2}/\text{s}^{2}=4.0{v’_{\text{B}}}^{2}+1.0{v’_{\text{C}}}^{2}\label{2-3}\tag{11}
\end{gather}
となる。
よって(\ref{2-1})~(\ref{2-3})より、求める速さは\(\boxed{v’_{\text{C}}=0.8\,\text{m/s}}\)となる。
(\ref{2-1})より
\begin{gather}
8.0v’_{\text{B}}\cos\theta_{\text{B}}=8.0\,\text{m/s}-v’_{\text{C}}\\
64{v’_{\text{B}}}^{2}\cos^{2}\theta_{\text{B}}=(8.0\,\text{m/s}-v’_{\text{C}})^{2} \label{a1}\tag{a1}
\end{gather}
となる。さらに(\ref{2-2})より
\begin{gather}
8.0v’_{\text{B}}\sin\theta_{\text{B}}=\sqrt{3}\,v’_{\text{C}}\\
64{v’_{\text{B}}}^{2}\sin^{2}\theta_{\text{B}}=3{v’_{\text{C}}}^{2}\label{a2}\tag{a2}
\end{gather}
となる。よって(\ref{a1})と(\ref{a2})の両辺をそれぞれ足し上げると
\begin{gather}
64{v’_{\text{B}}}^{2}\cos^{2}\theta_{\text{B}}+64{v’_{\text{B}}}^{2}\sin^{2}\theta_{\text{B}}=(8.0\,\text{m/s}-v’_{\text{C}})^{2}+3{v’_{\text{C}}}^{2}\\
64{v’_{\text{B}}}^{2}=64\,\text{m}^{2}/\text{s}^{2}-16v’_{\text{C}}+4{v’_{\text{C}}}^{2} \label{a3}\tag{a3}
\end{gather}
となる。
さらに(\ref{2-3})より
\begin{gather}
{v’_{\text{B}}}^{2}=\frac{4.0\,\text{m}^{2}/\text{s}^{2}-1.0{v’_{\text{C}}}^{2}}{4.0} \label{a4}\tag{a4}
\end{gather}
となるため、(\ref{a4})を(\ref{a3})に代入して整理すると
\begin{gather}
64\times\frac{4.0\,\text{m}^{2}/\text{s}^{2}-1.0{v’_{\text{C}}}^{2}}{4.0}=64\,\text{m}^{2}/\text{s}^{2}-16v’_{\text{C}}+4{v’_{\text{C}}}^{2}\\
64\,\text{m}^{2}/\text{s}^{2}-16{v’_{\text{C}}}^{2}=64\,\text{m}^{2}/\text{s}^{2}-16v’_{\text{C}}+4{v’_{\text{C}}}^{2}\\
20{v’_{\text{C}}}^{2}-16v’_{\text{C}}=0\\
5{v’_{\text{C}}}^{2}-4v’_{\text{C}}=0\\
v’_{\text{C}}(5v’_{\text{C}}-4)=0\\
\therefore v’_{\text{C}}=0\,\text{m/s},0.8\,\text{m/s}
\end{gather}
となる。よって\(v’_{\text{C}}\neq 0\)より\( v’_{\text{C}}=0.8\,\text{m/s}\)となる。
(3)
小球Cの質量を\(m_{\text{C}}\)とし、衝突前の速さを\(v_{\text{C}}\)、衝突後の速さを\(v’_{\text{C}}\)とする。
また、小球Bの衝突前の進行方向と水平方向がなす角度を\(\theta_{\text{C}}\)、衝突後の進行方向と水平方向がなす角度を\(\theta’_{\text{C}}\)とする(右図)。
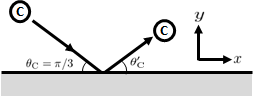
さらに、衝突前の水平方向の速さを\(v_{\text{C}x}\)、衝突前の鉛直方向の速さを\(v_{\text{C}y}\)、衝突後の水平方向の速さを\(v’_{\text{C}x}\)、衝突後の鉛直方向の速さを\(v’_{\text{C}y}\)とする。
Cと壁の衝突は「片方が動かない2物体間の衝突」であるため、反発係数の式(\ref{kabe1})を利用する。
よって(\ref{kabe1})より
\begin{gather}
e_{2}=-\frac{v’_{\text{C}y}}{v_{\text{C}y}}\\
\frac{1}{\sqrt{3}}=-\frac{v’_{\text{C}}\sin\theta’_{\text{C}}}{v_{\text{C}}\sin\theta_{\text{C}}}\\
\frac{1}{\sqrt{3}}=-\frac{v’_{\text{C}}\sin\theta’_{\text{C}}}{0.8\,\text{m/s}\times\displaystyle{\sin\frac{\pi}{3}}}\\
-\frac{1}{\sqrt{3}}\times 0.8\,\text{m/s}\times\frac{\sqrt{3}}{2}=v’_{\text{C}}\sin\theta’_{\text{C}}\\
v’_{\text{C}}\sin\theta’_{\text{C}}=-0.4\,\text{m/s}\label{3-1}\tag{12}
\end{gather}
となる。
さらに壁は滑らかであり、衝突時に摩擦力が発生せず速度の水平成分は変化しないため、
\begin{gather}
v_{\text{C}x}=v’_{\text{C}x}\\
v_{\text{C}}\cos\theta_{\text{C}}=v’_{\text{C}}\cos\theta’_{\text{C}}\\
0.8\,\text{m/s}\times\cos\frac{\pi}{3}=v’_{\text{C}}\cos\theta’_{\text{C}}\\
v’_{\text{C}}\cos\theta’_{\text{C}}=0.4\,\text{m/s}\label{3-2}\tag{13}
\end{gather}
となる。
よって(\ref{3-1})、(\ref{3-2})より、求める速さは\(\boxed{v’_{\text{C}}=0.4\sqrt{2}\,\text{m/s}}\)となる。
終わりに
外力がはたらかない系については、上の問題で解き方をマスターすれば他でも応用が効くだろう。
次回は外力がはたらく場合として、重力が加わる問題を見ていこうと思う。
次回はこちら。





コメント