前回
にて、球殻に閉じ込められた自由粒子のエネルギー固有値を求める問題を扱った。
今回は同じ三次元自由粒子でもより初等的な系である、箱型ポテンシャル中の三次元自由粒子を扱う。
(本来だったらこれが①の方が相応しい。)
無限井戸型ポテンシャル中の一次元自由粒子を、三次元系に拡張したものと考えれば良い。
問題
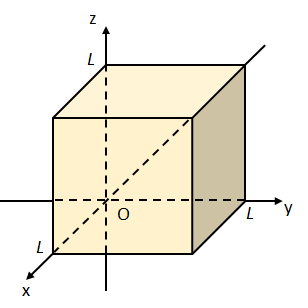
デカルト座標系において\((0,0,0)\),\((L,0,0)\), \((0,L,0)\), \((0,0,L)\), \((L,L,0)\), \((0,L,L)\), \((L,0,L)\), \((L,L,L)\)を頂点とする、一辺の長さが\(L\)の立方体を考える。
さらに立方体の面は無限大のポテンシャル障壁となっており、この立方体内に質量\(m\)の自由粒子が一つあるとする。
このとき、粒子の定常状態に対応する波動関数を\(\varphi(\vec{r})\)とし、\(\varphi(\vec{r})\)に対応するエネルギー固有値を\(E\)とすると、定常状態のシュレディンガー方程式は
\begin{align}
-\frac{\hbar^{2}}{2m}\triangle\varphi(\vec{r})=E\varphi(\vec{r}) \tag{1}\label{自由粒子Scheq}
\end{align}
となる。
このとき、自由粒子の波動関数\(\varphi(\vec{r})\)とそれに対応するエネルギー固有値を\(E\)を求めよ。
解答
立方体の面は無限大のポテンシャル障壁となっているため、障壁の外側に粒子が存在する確率は0である。
よって境界条件は
\begin{align}
&\varphi(0,y,z)=\varphi(x,0,z)=\varphi(x,y,0)\\
=&\varphi(L,y,z)=\varphi(x,L,z)=\varphi(x,y,L)=0 \tag{2}\label{自由粒子境界条件}
\end{align}
で与えられる。
この場合、波動関数\(\varphi(\vec{r})\)を\(\varphi(\vec{r})=f(x)g(y)h(z)\)のような変数分離系の形で書き、\(E=E_{x}+E_{y}+E_{z}\)とすれば
\begin{align}
-\frac{\hbar^{2}}{2m}\frac{d^{2}}{dx^{2}}f(x)=E_{x}f(x) \tag{3}\label{一次元Sch}
\end{align}
という一次元の自由粒子の問題に帰着させることができる。
さらに境界条件(\ref{自由粒子境界条件})は、
\begin{align}
f(0)=f(L)=g(0)=g(L)=h(0)=h(L)=0 \tag{4}\label{自由粒子境界条件2}
\end{align}
と書き直すことができる。
ここで、下記2点を考慮すると\(E_{x}>0\)となり、(\ref{一次元Sch})の解は振動解となることがわかる。
・エネルギー固有状態、エネルギー固有値の一般的な事実「\(E\)は定数であり、\(E\ge V_{\text{min}}\)(一般的なポテンシャル\(V(\vec{r})\)の最小値)を満たす」
・\(E_{x}=0\)のときは\(f(x)=0\)となるため不適。
よって境界条件\(f(0)=0\)を使い、\(k_{x}\)を\(x\)方向における波数、\(A\)を任意定数とすれば、\(f(x)\)は
\begin{align}
f(x)=A\sin(k_{x}x) \tag{5}\label{解1}
\end{align}
とおける。
このとき、この(\ref{解1})を(\ref{一次元Sch})に代入して計算すると、
\begin{align}
&-\frac{\hbar^{2}}{2m}\frac{d^{2}}{dx^{2}}A\sin(k_{x}x)=E_{x}A\sin(k_{x}x) \notag \\
&\frac{\hbar^{2}k_{x}^{2}}{2m}\sin(k_{x}x)=E_{x}\sin(k_{x}x) \notag \\
&E_{x}=\frac{\hbar^{2}k_{x}^{2}}{2m} \tag{6}\label{xのエネルギー}
\end{align}
となる。
ここで\(k_{x}\)を具体的に求める。
境界条件\(f(L)=0\)より、
\begin{align}
&f(L)=A\sin(k_{x}L)=0 \notag \\
&\sin(k_{x}L)=0 \notag \\
&k_{x}L=n_{x}\pi \qquad \therefore\,k_{x}=\frac{n_{x}\pi}{L}\quad\text{(ただし$n_{x}\in\mathbb{N}$)} \tag{7}\label{kxの表式}
\end{align}
となる。
補足
勿論、数学的には\(n_{x}\in\mathbb{Z}\)でも成立する。
しかし\(n_{x}=0\)の場合は全領域で\(\varphi(\vec{r})=0\)となって規格化条件を満たさない。
さらに\(n_{x}=-1,-2,\cdots\)の場合の解は\(n_{x}=1,2,\cdots\)の場合の解の定数倍(符号が変わるだけ)であるため、定数倍の原理から物理的状態は同じである。
よってこれらの解は物理的に許されず除外される。
同様の理由で、この後登場する\(n_{y}\)も\(n_{y}\in\mathbb{N}\)となる。
よってこの(\ref{kxの表式})を(\ref{xのエネルギー})に代入すると、
\begin{align}
E_{x}=\frac{\hbar^{2}}{2m}\left(\frac{n_{x}\pi}{L}\right)^{2}=\frac{\pi^{2}\hbar^{2}}{2mL^{2}}n_{x}^{2} \tag{8}\label{xのエネルギー2}
\end{align}
となる。
最後に規格化条件\(\int_{0}^{L}|f(x)|^{2}dx=1\)を計算して\(A\)を求める。
まず(\ref{解1})より、
\begin{align}
\int_{0}^{L}|f(x)|^{2}dx=\int_{0}^{L}A^{2}\sin^{2}(k_{x}x)dx \tag{9}
\end{align}
となる。
ここで三角関数の倍角公式と(\ref{kxの表式})を使えば
\begin{align}
\int_{0}^{L}|f(x)|^{2}dx &=A^{2}\int_{0}^{L}\frac{1}{2}\{1-\cos(2k_{x}x)\}dx \\
&=\frac{A^{2}}{2}\left[x-\frac{L}{2n_{x}\pi}\sin\left(\frac{2n_{x}\pi}{L}x\right)\right]^{L}_{0}=\frac{A^{2}L}{2} \tag{10}\label{規格化1}
\end{align}
となる。
よって(\ref{規格化1})の最右辺が1となるため、
\begin{align}
\frac{A^{2}L}{2}=1 \qquad \therefore\,A=\sqrt{\frac{2}{L}} \tag{11}\label{Aの表式}
\end{align}
となる。
よって(\ref{kxの表式})と(\ref{Aの表式})を(\ref{解1})に代入すれば、
\begin{align}
f(x)=\sqrt{\frac{2}{L}}\sin\left(\frac{n_{x}\pi}{L}x\right) \qquad \text{(ただし$n_{x}\in\mathbb{N}$)} \tag{12}\label{真のfx}
\end{align}
となる。
よって対称性を利用すれば、\(f(x)\)と同様にして\(g(y)\)、\(h(z)\)は
\begin{align}
g(y)=\sqrt{\frac{2}{L}}\sin\left(\frac{n_{y}\pi}{L}y\right),\qquad h(z)=\sqrt{\frac{2}{L}}\sin\left(\frac{n_{z}\pi}{L}z\right)\qquad \text{(ただし$n_{y},n_{z}\in\mathbb{N}$)} \tag{13}\label{yzの波動関数}
\end{align}
と求められ、\(E_{y}\)、\(E_{z}\)は
\begin{align}
E_{y}=\frac{\hbar^{2}k_{y}^{2}}{2m}=\frac{\pi^{2}\hbar^{2}}{2mL^{2}}n_{y}^{2}, \qquad E_{z}=\frac{\hbar^{2}k_{z}^{2}}{2m}=\frac{\pi^{2}\hbar^{2}}{2mL^{2}}n_{z}^{2} \tag{14}\label{yzのエネルギー}
\end{align}
となる。
以上より、全体の波動関数\(\varphi(\vec{r})\)と全体のエネルギー\(E\)は\(n_{x},n_{y},n_{z}\in\mathbb{N}\)として
\begin{align}
&\boxed{\varphi(\vec{r})=\left(\frac{2}{L}\right)^{\frac{3}{2}}\sin\left(\frac{n_{x}\pi}{L}x\right)\sin\left(\frac{n_{y}\pi}{L}y\right)\sin\left(\frac{n_{z}\pi}{L}z\right)} \tag{15}\label{全体の波動関数} \\
&\boxed{E=\frac{\pi^{2}\hbar^{2}}{2mL^{2}}(n_{x}^{2}+n_{y}^{2}+n_{z}^{2})} \tag{16}\label{全体のエネルギー}
\end{align}
となる。
この結果から、箱型ポテンシャル中の自由粒子の定常状態は三つの自然数の組\((n_{x},n_{y},n_{z})\)によって指定され、ラベル付けすることができることがわかる。
終わりに
箱型ポテンシャル中の三次元自由粒子は最も初等的な問題であるため、最終的には空で解ける状態になっておくのが望ましい。
派生問題としては、ある軸方向では周期境界ポテンシャルになっているものもある。
慣れるまでいくつか類題を解いておくと良いだろう。
END





コメント