前回
に引き続き、一次元での定常状態の一粒子系の例題を解いていく。
今回はデルタ関数型ポテンシャルが存在する系を考えていく。
問題
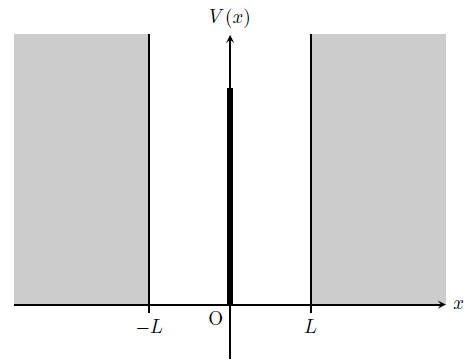
右図のように、\(x=\pm L\)に無限大のポテンシャル障壁、\(x=0\)に面積\(v_{0}\)のデルタ関数型ポテンシャルがあり、その内部にある自由粒子を考える。
このとき、この粒子に関する定常状態のシュレディンガー方程式は下記のように書ける。
\begin{align}
-\frac{{\hbar}^{2}}{2m}{\varphi}”(x)+v_{0}\delta(x)\varphi(x)=E\varphi(x) \tag{1}\label{for.3.2.1}
\end{align}
このとき、以下の問いに答えよ。
(a) \(v_{0}=0\)のとき、基底状態の波動関数\(\varphi_{1}^{(0)}(x)\)とエネルギー\(E_{1}^{(0)}\)、および第一励起状態の波動関数\(\varphi_{2}^{(0)}(x)\)とエネルギー\(E_{2}^{(0)}\)を求めよ。
(b) \(v_{0}\geq 0\)のとき、\(x\)の反転に対して反対称な解のうち、エネルギーが最小となる波動関数とエネルギー固有値を求めよ。ただし、波動関数は規格化すること。
(c) \(v_{0}\geq 0\)のとき、\(x\)の反転に対して対称な波動関数に対応するエネルギー固有値\(E\)を決める条件式を求めよ。また\(v_{0}\ll 1\)のとき、エネルギー固有値の最小値が(a)で求めた\(E_{1}^{(0)}\)に近づくことを確認せよ。
ただし、式(\ref{for.3.2.1})の解は原点で接続条件\(\varphi(+0)=\varphi(-0),\,\varphi'(+0)=\varphi'(-0)+(2mv_{0}/\hbar^{2})\varphi(0)\)を満たすことを利用してよい。
解答(a)
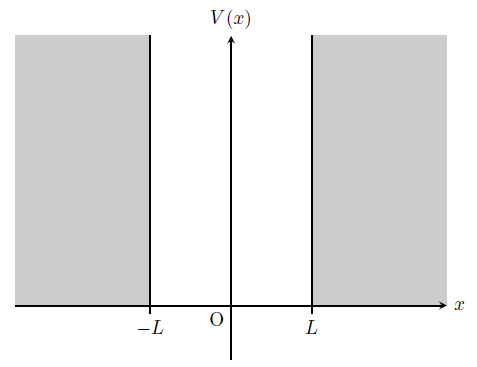
\(v_{0}=0\)のとき、シュレディンガー方程式(\ref{for.3.2.1})はデルタ関数型ポテンシャルの項が消え、次式のように書き直すことができる。
\begin{align}
-\frac{{\hbar}^{2}}{2m}{\varphi}”(x)=E\varphi(x) \tag{2}\label{for.3.2.2}
\end{align}
すなわち右図のように、無限大のポテンシャル障壁によって閉じ込められた自由粒子を考えれば良い。
式(\ref{for.3.2.2})を変形すると次式のようになる。
\begin{align}
&{\varphi}”(x)=-\frac{2mE}{{\hbar}^{2}}\varphi(x) \notag \\
&{\varphi}”(x)=-\varepsilon\varphi(x) \qquad (\varepsilon=\frac{2mE}{{\hbar}^{2}}>0) \tag{3}\label{for.3.2.3}
\end{align}
\(\varepsilon>0\)となるのは\(E>0\)となるためである。
(一次元での定常状態の一粒子系では、外部ポテンシャルの最小値\(V_{\text{min}}\)に対して常に\(E>V_{\text{min}}\)が成立する。)
よって(\ref{for.3.2.3})の一般解は、\(A,B\)を複素任意定数として次式のように書ける。
\begin{align}
\varphi(x)=A\cos(\sqrt{\varepsilon}x)+B\sin(\sqrt{\varepsilon}x) \tag{4}\label{for.3.2.4}
\end{align}
となる。
ここからは、外部ポテンシャルが対称(\(V(x)=V(-x)=0\))であることを利用し、対称解と反対称解を求めれば、全ての波動関数とエネルギー固有値を求めることができる。
詳細な計算過程は省略するが、最終的に、
\begin{align}
\begin{cases}
基底状態:\displaystyle{\varphi_{1}^{(0)}(x)=\sqrt{\frac{1}{L}}\cos\left(\frac{\pi}{2L}x\right),\qquad E_{1}^{(0)}=\frac{\pi^{2}\hbar^{2}}{2m(2L)^{2}}}\\
\quad\\
第一励起状態:\displaystyle{\varphi_{2}^{(0)}(x)=\sqrt{\frac{1}{L}}\sin\left(\frac{\pi}{L}x\right),\qquad E_{2}^{(0)}=\frac{4\pi^{2}\hbar^{2}}{2m(2L)^{2}}}
\end{cases}
\end{align}
となる。
解答(b)
\(v_{0}\geq 0\)のとき、\(-L{\leq}x<0\)および\(0<x{\leq}L\)ではポテンシャルが存在しないため、シュレディンガー方程式は式(\ref{for.3.2.2})と同じ形となる。
よって(a)と同様に考えると、各範囲における式(\ref{for.3.2.2})の一般解は\(C_{1},D_{1},C_{2},D_{2}\)を複素任意定数として次式のように書ける。
\begin{align}
\begin{cases}
\varphi(x)=C_{1}\cos(\sqrt{\varepsilon}x)+D_{1}\sin(\sqrt{\varepsilon}x) &\text{($-L{\leq}x<0$のとき)} \\
\varphi(x)=C_{2}\cos(\sqrt{\varepsilon}x)+D_{2}\sin(\sqrt{\varepsilon}x) &\text{($0<x{\leq}L$のとき)} \\
\end{cases}\tag{5}\label{for.3.2.10}
\end{align}
まずは反対称な解(波動関数)を考える。
このとき、解(\ref{for.3.2.10})は次式のように書き直せる。
\begin{align}
\begin{cases}
\varphi(x)=C_{1}\cos(\sqrt{\varepsilon}x)+D_{1}\sin(\sqrt{\varepsilon}x) &\text{($-L{\lle}x<0$のとき)} \\
\varphi(x)=-C_{1}\cos(\sqrt{\varepsilon}x)+D_{1}\sin(\sqrt{\varepsilon}x) &\text{($0<x{\lle}L$のとき)} \\
\end{cases}\tag{6}\label{for.3.2.111}
\end{align}
さらに解(\ref{for.3.2.111})の1階微分は次式のようになる。
\begin{align}
\begin{cases}
\varphi'(x)=-C_{1}\sqrt{\varepsilon}\sin(\sqrt{\varepsilon}x)+D_{1}\sqrt{\varepsilon}\cos(\sqrt{\varepsilon}x) &\text{($-L{\lle}x<0$のとき)} \\
\varphi'(x)=C_{1}\sqrt{\varepsilon}\sin(\sqrt{\varepsilon}x)+D_{1}\sqrt{\varepsilon}\cos(\sqrt{\varepsilon}x) &\text{($0<x{\lle}L$のとき)} \\
\end{cases}\tag{7}\label{for.3.2.112}
\end{align}
ここでまず原点(\(x=0\))での接続条件を考える。
解(\ref{for.3.2.111})の\(-L{\leq}x<0\)での\(\varphi(x)\)から\(\varphi(-0)\)を、\(0<x{\leq}L\)での\(\varphi(x)\)から\(\varphi(+0)\)をそれぞれ求めると、
\begin{align}
\begin{cases}
\varphi(-0)=C_{1}\cdot 1+D_{1}\cdot 0 &\therefore\varphi(-0)=C_{1} \\
\varphi(+0)=-C_{1}\cdot 1+D_{1}\cdot 0 &\therefore\varphi(+0)=-C_{1} \\
\end{cases}\tag{8}\label{for.3.2.16}
\end{align}
となるため、式(\ref{for.3.2.16})を原点(\(x=0\))での接続条件\(\varphi(+0)=\varphi(-0)\)に代入すると、
\begin{align}
&C_{1}=-C_{1} &\therefore C_{1}=0 \tag{9}\label{for.3.2.17}
\end{align}
となる。
よって式(\ref{for.3.2.17})を式(\ref{for.3.2.111})、(\ref{for.3.2.112})に代入すると、\(-L{\leq}x<0,0<x{\leq}L\)のいずれの範囲でも、
\begin{align}
\begin{cases}
\varphi(x)=D_{1}\sin(\sqrt{\varepsilon}x) \\
\varphi'(x)=D_{1}\sqrt{\varepsilon}\cos(\sqrt{\varepsilon}x) \\
\end{cases}\tag{10}\label{for.3.2.18}
\end{align}
となることがわかる。
あとは1階微分に関する接続条件\(\varphi'(+0)=\varphi'(-0)+(2mv_{0}/\hbar^{2})\varphi(0)\)を満たせば、\(x=0\)で波動関数が滑らかに接続するのだが、式(\ref{for.3.2.18})から
\begin{align}
\begin{cases}
\varphi(0)=D_{1}\cdot 0 &\therefore\varphi(0)=0 \\
\varphi'(+0)=D_{1}\sqrt{\varepsilon}\cdot 1 &\therefore\varphi'(+0)=D_{1}\sqrt{\varepsilon} \\
\varphi'(-0)=D_{1}\sqrt{\varepsilon}\cdot 1 &\therefore\varphi'(-0)=D_{1}\sqrt{\varepsilon} \\
\end{cases}\tag{11}\label{for.3.2.19}
\end{align}
となり、接続条件\(\varphi'(+0)=\varphi'(-0)+(2mv_{0}/\hbar^{2})\varphi(0)\)を満足していることがわかる。
以上から反対称な解(波動関数)は、
\begin{align}
\varphi(x)=D_{1}\sin(\sqrt{\varepsilon}x) \tag{12}\label{for.3.2.20}
\end{align}
となる。
実はこの(\ref{for.3.2.20})は、(a)で求めた自由粒子における反対称な解と同形である。
よって(a)と同様にして波動関数とエネルギー固有値を求めればよい。
最終的に、求める波動関数とエネルギー固有値は
\begin{align}
\begin{cases}
波動関数:\displaystyle{\varphi(x)=\sqrt{\frac{1}{L}}\sin\left(\frac{\pi}{L}x\right)}\\
エネルギー固有値:\displaystyle{E=\frac{4\pi^{2}\hbar^{2}}{2m(2L)^{2}}}
\end{cases}
\end{align}
となり、エネルギー固有値は\(E_{2}^{(0)}\)と同値となる。
解答(c)
今回は対称な解(波動関数)を考えるため、解(\ref{for.3.2.10})は次式のように書き直せる。
\begin{align}
\begin{cases}
\varphi(x)=C_{1}\cos(\sqrt{\varepsilon}x)+D_{1}\sin(\sqrt{\varepsilon}x) &\text{(\(-L{\leq}x<0\)のとき)} \\
\varphi(x)=C_{1}\cos(\sqrt{\varepsilon}x)-D_{1}\sin(\sqrt{\varepsilon}x) &\text{(\(0<x{\leq}L\)のとき)} \\
\end{cases}\tag{13}\label{for.3.2.11}
\end{align}
さらに解(\ref{for.3.2.11})の1階微分は次式のようになる。
\begin{align}
\begin{cases}
\varphi'(x)=-C_{1}\sqrt{\varepsilon}\sin(\sqrt{\varepsilon}x)+D_{1}\sqrt{\varepsilon}\cos(\sqrt{\varepsilon}x) &\text{(\(-L{\leq}x<0\)のとき)} \\
\varphi'(x)=-C_{1}\sqrt{\varepsilon}\sin(\sqrt{\varepsilon}x)-D_{1}\sqrt{\varepsilon}\cos(\sqrt{\varepsilon}x) &\text{(\(0<x{\leq}L\)のとき)} \\
\end{cases}\tag{14}\label{for.3.2.12}
\end{align}
ここで原点(\(x=0\))での接続条件を考える。
まず解(\ref{for.3.2.11})の各式に\(x=0\)を代入すると、いずれも\(\varphi(0)=C_{1}\)となり、\(\varphi(x)\)は原点で連続であることを確認することができる。
続いて、1階微分に関する接続条件\(\varphi'(+0)=\varphi'(-0)+(2mv_{0}/\hbar^{2})\varphi(0)\)を考える。
式(\ref{for.3.2.12})の\(-L{\leq}x<0\)での\(\varphi'(x)\)から\(\varphi'(-0)\)を、\(0<x{\leq}L\)での\(\varphi'(x)\)から\(\varphi'(+0)\)をそれぞれ求めると、
\begin{align}
\begin{cases}
\varphi'(-0)=-C_{1}\sqrt{\varepsilon}\cdot 0+D_{1}\sqrt{\varepsilon}\cdot 1 &\therefore\varphi'(-0)=D_{1}\sqrt{\varepsilon} \\
\varphi'(+0)=-C_{1}\sqrt{\varepsilon}\cdot 0-D_{1}\sqrt{\varepsilon}\cdot 1 &\therefore\varphi'(+0)=-D_{1}\sqrt{\varepsilon} \\
\end{cases}\tag{15}\label{for.3.2.13}
\end{align}
となるため、式(\ref{for.3.2.13})および\(\varphi(0)=C_{1}\)を接続条件\(\varphi'(+0)=\varphi'(-0)+(2mv_{0}/\hbar^{2})\varphi(0)\)に代入すると、
\begin{align}
&-D_{1}\sqrt{\varepsilon}=D_{1}\sqrt{\varepsilon}+\frac{2mv_{0}}{\hbar^{2}}C_{1} \notag \\
&2D_{1}\sqrt{\varepsilon}=-\frac{2mv_{0}}{\hbar^{2}}C_{1} &\therefore\frac{D_{1}}{C_{1}}=-\frac{mv_{0}}{\sqrt{\varepsilon}\hbar^{2}} \tag{16}\label{for.3.2.14}
\end{align}
となる。
さらに境界条件\(\varphi(-L)=\varphi(L)=0\)を式(\ref{for.3.2.11})に適用すると、
\begin{align}
&C_{1}\cos(-\sqrt{\varepsilon}L)+D_{1}\sin(-\sqrt{\varepsilon}L)=C_{1}\cos(\sqrt{\varepsilon}L)-D_{1}\sin(\sqrt{\varepsilon}L)=0 \notag \\
&C_{1}\cos(\sqrt{\varepsilon}L)-D_{1}\sin(\sqrt{\varepsilon}L)=0 \qquad \text{(一般に$\cos(-x)=\cos{x},\sin(-x)=-\sin{x}$より)}\notag \\
&\therefore\frac{D_{1}}{C_{1}}=\frac{1}{\tan(\sqrt{\varepsilon}L)} \tag{17}\label{for.3.2.15}
\end{align}
となる。
以上より、求める関係式は式(\ref{for.3.2.14})、(\ref{for.3.2.15})から次式のようになる。
\begin{align}
\boxed{\tan(\sqrt{\varepsilon}L)=-\frac{\hbar^{2}}{mv_{0}}\sqrt{\varepsilon}} \qquad \text{(ただし\(\varepsilon=\frac{2mE}{{\hbar}^{2}}>0\))} \tag{18}\label{kai2-1}
\end{align}
ここで\(v_{0}\ll 1\)の場合を考えると、(\ref{kai2-1})の右辺が\(-\infty\)に近づく。よって
\begin{align}
&\tan(\sqrt{\varepsilon}L) \to -\infty \notag \\
&\sqrt{\varepsilon}L\simeq\frac{n}{2}\pi \qquad (n=1,3,5,\cdots) \notag \\
&\sqrt{\varepsilon}\simeq\frac{n}{2L}\pi \notag \\
&\sqrt{\frac{2mE}{\hbar}}\simeq\frac{n}{2L}\pi \qquad \text{($\varepsilon=\frac{2mE}{\hbar}$より)} \notag \\
&\frac{2mE}{\hbar}\simeq\left(\frac{n}{2L}\pi\right)^{2} \qquad \therefore E\simeq\frac{\pi^{2}\hbar^{2}}{2m(2L)^{2}}n^{2} \quad (n=1,3,5,\cdots) \tag{19}\label{for.3.2.31}
\end{align}
となる。
よって式(\ref{for.3.2.31})において\(n=1\)のとき最小のエネルギー固有値をとるため、求める最小のエネルギー固有値は、
\begin{align}
E\simeq\frac{\pi^{2}\hbar^{2}}{2m(2L)^{2}}\cdot 1 \qquad \boxed{E\simeq\frac{\pi^{2}\hbar^{2}}{2m(2L)^{2}}} \notag
\end{align}
となり、\(E_{1}^{(0)}\)に近づくことがわかる。
これはよくよく考えると妥当な結果である。
\(v_{0}\ll 1\)の場合とは、デルタ関数型ポテンシャルがほぼ0に近い状態、すなわち(a)の設定に近い状態である。
今回は対称解を考えているため、今回の結果で最小のエネルギー固有値をとる状態は、(a)の対称解で最小のエネルギー固有値をとる状態、すなわち基底状態に対応することがわかる。
終わりに
今回は天下り式に、デルタ関数型ポテンシャルにおける接続条件を提示したが、また別の機会にこの接続条件の導出についても書こうと思う。
次に量子力学をやるとしたら何だろうか?
調和振動子、水素原子、摂動論…
いずれにしても勉強し直さないとな…
END





コメント