行列を用いた代表的な応用として回転が挙げられる。
高校数学でも、x-y平面上の点の原点まわりの回転移動が
\begin{align}
\begin{pmatrix}x_{2}\\ y_{2}\end{pmatrix}=
\begin{pmatrix}\cos\theta & -\sin\theta \\ \sin\theta & \cos\theta\end{pmatrix}
\begin{pmatrix}x_{1}\\ y_{1}\end{pmatrix}
\end{align}
で表されることを習った人もいるだろう。
今回はこの回転行列を3次元に拡張し、原点を通る任意の軸まわりの回転を表現できるロドリゲスの回転公式を見ていく。
ロドリゲスの回転公式
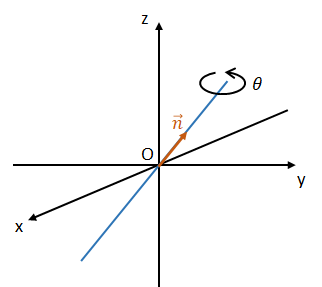
3次元デカルト座標系において原点を通る直線があり、この直線を回転軸として角度\(\theta\)だけ回転させる作用を考える。
このとき、軸の向き(回転に対して右ねじが進む向き)を表す単位ベクトルを\(\vec{n}=(n_{1},n_{2},n_{3})^{\text{T}}\)とすると、回転作用を表す行列は
\begin{align}
\mathsf{R}(\theta)=\begin{pmatrix}n_{1}^{2}(1-\cos\theta)+\cos\theta&n_{1}n_{2}(1-\cos\theta)-n_{3}\sin\theta&n_{1}n_{3}(1-\cos\theta)+n_{2}\sin\theta\\ n_{1}n_{2}(1-\cos\theta)+n_{3}\sin\theta&n_{2}^{2}(1-\cos\theta)+\cos\theta&n_{2}n_{3}(1-\cos\theta)-n_{1}\sin\theta \\ n_{1}n_{3}(1-\cos\theta)-n_{2}\sin\theta&n_{2}n_{3}(1-\cos\theta)+n_{1}\sin\theta&n_{3}^{2}(1-\cos\theta)+\cos\theta\end{pmatrix}
\end{align}
と表せられ、これをロドリゲスの回転公式と呼ぶ。
この逆行列は逆回転を考えれば良いため、\(\cos(-\theta)=\cos\theta,\sin(-\theta),-\sin\theta\)を利用して整理すると、\(\mathsf{R}(\theta)\)の逆行列は
\begin{align}
\mathsf{R}(\theta)^{-1}=\begin{pmatrix}n_{1}^{2}(1-\cos\theta)+\cos\theta&n_{1}n_{2}(1-\cos\theta)+n_{3}\sin\theta&n_{1}n_{3}(1-\cos\theta)-n_{2}\sin\theta\\ n_{1}n_{2}(1-\cos\theta)-n_{3}\sin\theta&n_{2}^{2}(1-\cos\theta)+\cos\theta&n_{2}n_{3}(1-\cos\theta)+n_{1}\sin\theta \\ n_{1}n_{3}(1-\cos\theta)+n_{2}\sin\theta&n_{2}n_{3}(1-\cos\theta)-n_{1}\sin\theta&n_{3}^{2}(1-\cos\theta)+\cos\theta\end{pmatrix}
\end{align}
と書ける。
例題1
例題1
ロドリゲスの回転公式を利用して、x軸まわり、y軸まわり、z軸まわりの回転行列を導出せよ。
ただし回転角を\(\theta\)とし、軸の向き(回転に対して右ねじが進む向き)は各軸の正の向きとする。
解説
まずx軸まわりの回転行列を求める。
\(\vec{n}=(1,0,0)\)より、ロドリゲスの回転公式を利用するとx軸まわりの回転行列\(\mathsf{R}_{x}(\theta)\)は
\begin{gather}
\mathsf{R}_{x}(\theta)=\begin{pmatrix}
(1-\cos\theta)+\cos\theta & 0 & 0\\
0 & \cos\theta & -\sin\theta \\
0 & \sin\theta & \cos\theta
\end{pmatrix}=\begin{pmatrix}
1 & 0 & 0\\
0 & \cos\theta & -\sin\theta \\
0 & \sin\theta & \cos\theta
\end{pmatrix}\\
\boxed{\mathsf{R}_{x}(\theta)=\begin{pmatrix}
1 & 0 & 0\\
0 & \cos\theta & -\sin\theta \\
0 & \sin\theta & \cos\theta
\end{pmatrix}}
\end{gather}
となる。
続いてy軸まわりの回転行列を求める。
\(\vec{n}=(0,1,0)\)より、ロドリゲスの回転公式を利用するとy軸まわりの回転行列\(\mathsf{R}_{y}(\theta)\)は
\begin{gather}
\mathsf{R}_{y}(\theta)=\begin{pmatrix}
\cos\theta & 0 & \sin\theta\\
0 & (1-\cos\theta)+\cos\theta & 0 \\
-\sin\theta & 0 & \cos\theta
\end{pmatrix}=\begin{pmatrix}
\cos\theta & 0 & \sin\theta\\
0 & 1 & 0 \\
-\sin\theta & 0 & \cos\theta
\end{pmatrix}\\
\boxed{\mathsf{R}_{y}(\theta)=\begin{pmatrix}
\cos\theta & 0 & \sin\theta\\
0 & 1 & 0 \\
-\sin\theta & 0 & \cos\theta
\end{pmatrix}}
\end{gather}
となる。
最後にz軸まわりの回転行列を求める。
\(\vec{n}=(0,0,1)\)より、ロドリゲスの回転公式を利用するとy軸まわりの回転行列\(\mathsf{R}_{z}(\theta)\)は
\begin{gather}
\mathsf{R}_{z}(\theta)=\begin{pmatrix}
\cos\theta & -\sin\theta & 0\\
\sin\theta & \cos\theta & 0 \\
0 & 0 & (1-\cos\theta)+\cos\theta
\end{pmatrix}=\begin{pmatrix}
\cos\theta & -\sin\theta & 0\\
\sin\theta & \cos\theta & 0 \\
0 & 0 & 1
\end{pmatrix}\\
\boxed{\mathsf{R}_{z}(\theta)=\begin{pmatrix}
\cos\theta & -\sin\theta & 0\\
\sin\theta & \cos\theta & 0 \\
0 & 0 & 1
\end{pmatrix}}
\end{gather}
となる。
例題2
例題2
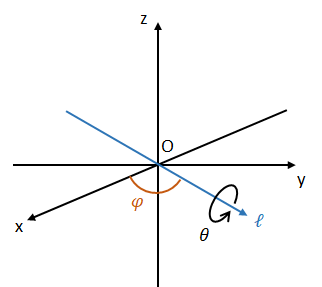
x軸をy軸の方向へ角度\(\varphi\)だけ回転させてできる軸を\(\ell\)と置く。
この軸\(\ell\)のまわりで角度\(\theta\)だけ回転させたとき、点A:\((\alpha,\beta,\gamma)\)が移動する点の座標を求めよ。
解説
まず軸\(\ell\)まわりの回転を表すロドリゲスの回転公式を求める。
軸\(\ell\)はx軸をy軸の方向へ角度\(\varphi\)だけ回転させてできるため、軸\(\ell\)の向きを表す単位ベクトルは\(\vec{n}=(\cos\varphi,\sin\varphi,0)\)となる。
よって軸\(\ell\)まわりの回転を表すロドリゲスの回転公式\(\mathsf{R}_{\ell}(\theta)\)は
\begin{gather}
\mathsf{R}_{\ell}(\theta)=\begin{pmatrix}
\cos^{2}\varphi(1-\cos\theta)+\cos\theta & \cos\varphi\sin\varphi(1-\cos\theta) & \sin\varphi\sin\theta \\
\cos\varphi\sin\varphi(1-\cos\theta) & \sin^{2}\varphi(1-\cos\theta)+\cos\theta & -\cos\varphi\sin\theta \\
-\sin\varphi\sin\theta & \cos\varphi\sin\theta & \cos\theta
\end{pmatrix}
\end{gather}
となる。
よって、この回転によって点A:\((\alpha,\beta,\gamma)\)が移動する点の座標は
\begin{gather}
&\begin{pmatrix}
\cos^{2}\varphi(1-\cos\theta)+\cos\theta & \cos\varphi\sin\varphi(1-\cos\theta) & \sin\varphi\sin\theta \\
\cos\varphi\sin\varphi(1-\cos\theta) & \sin^{2}\varphi(1-\cos\theta)+\cos\theta & -\cos\varphi\sin\theta \\
-\sin\varphi\sin\theta & \cos\varphi\sin\theta & \cos\theta
\end{pmatrix}\begin{pmatrix}\alpha \\ \beta \\ \gamma\end{pmatrix}\\
=&\boxed{\begin{pmatrix}\alpha\{\cos^{2}\varphi(1-\cos\theta)+\cos\theta\}+\beta\cos\varphi\sin\varphi(1-\cos\theta)+\gamma\sin\varphi\sin\theta \\
\alpha\cos\varphi\sin\varphi(1-\cos\theta)+\beta\{\sin^{2}\varphi(1-\cos\theta)+\cos\theta\}-\gamma\cos\varphi\sin\theta \\
-\alpha\sin\varphi\sin\theta+\beta\cos\varphi\sin\theta+\gamma\cos\theta\end{pmatrix}}
\end{gather}
となる。
終わりに
この公式、仕事でデータの解析をする際に「あったら便利だなぁ」くらいのノリで調べて初めて知ったものだ。
3次元系の回転行列の一般形なので、大学で数学を勉強しているときに味わった「ちょっと得をした気分」を久々に味わっている。
(一般化された公式はあらゆる場面で使えるので、それ1つをものにするだけで幅広く応用がきく。)
数学に関しては今後を見据えて統計学と情報理論あたりを勉強したいが、今は長期にわたる最重要タスクを抱えていて最短でも2~3か月後にならないと落ち着いて勉強ができそうにない。
なんて言い訳している時点でアカンのかもしれんが…
END




コメント