【微積分】多重積分⑤～問題演習②(逐次積分②)～

　前回

からの続き。

　今回も逐次積分の問題演習だが、積分領域の与えられ方が前回とは異なり、自分で計算式を立式する必要があるので注意。

被積分関数が変数分離できる場合

解説

(1)

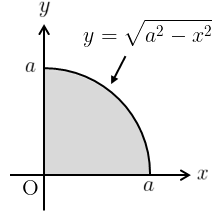
　積分領域は右図のようになり、求める積分は

\begin{align}
\int_{0}^{a}dx\int_{0}^{\sqrt{a^{2}-x^{2}}}dy\,xy
\end{align}

となる。

　まず\(y\)での積分が\(x\)に依存しているため、\(y\)での積分から実行して

\begin{align}
\int_{0}^{a}dx\int_{0}^{\sqrt{a^{2}-x^{2}}}dy\,xy&=\int_{0}^{a}dx\,x\biggl[\frac{1}{2}y^{2}\biggr]_{0}^{\sqrt{a^{2}-x^{2}}}\notag \\
&=\frac{1}{2}\int_{0}^{a}dx\,x(a^{2}-x^{2}) \notag
\end{align}

となる。

　続いて\(x\)で積分する。

\begin{align}
\frac{1}{2}\int_{0}^{a}dx\,x(a^{2}-x^{2})&=\frac{1}{2}\biggl[\frac{a^{2}}{2}x^{2}-\frac{1}{4}x^{4}\biggr]_{0}^{a} \notag \\
&=\frac{1}{2}\left(\frac{a^{4}}{2}-\frac{a^{4}}{4}\right)=\boxed{\frac{a^{4}}{8}}
\end{align}

　

(2)

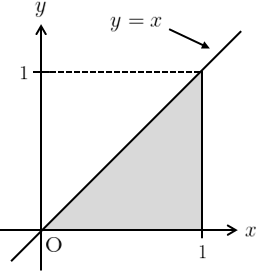
　積分領域は右図のようになり、求める積分は

\begin{align}
\int_{0}^{1}dx\int_{0}^{x}dy\,x\tan^{-1}y
\end{align}

となる。

　まず\(y\)での積分が\(x\)に依存しているため、\(y\)での積分から実行する。\(f(y)=\tan^{-1}y,\,g(y)=y\)として部分積分法を用いて

\begin{align}
&\int_{0}^{1}dx\int_{0}^{x}dy\,x\tan^{-1}y\\
=&\int_{0}^{1}dx\,x\left\{\biggl[y\tan^{-1}y\biggr]_{0}^{x}-\int_{0}^{x}dy\frac{y}{1+y^{2}}\right\} \notag \\
=&\int_{0}^{1}dx\,x\left\{x\tan^{-1}x-\left[\frac{1}{2}\log(1+y^{2})\right]_{0}^{x}\right\} \notag \\
=&\int_{0}^{1}dx\,\left\{x^{2}\tan^{-1}x-\frac{1}{2}x\log(1+x^{2})\right\}
\end{align}

となる。

　次に\(x\)で積分する。

\begin{align}
\int_{0}^{1}dx\,\left\{x^{2}\tan^{-1}x-\frac{1}{2}x\log(1+x^{2})\right\}&=\int_{0}^{1}dx\,x^{2}\tan^{-1}x-\frac{1}{2}\int_{0}^{1}dx\,x\log(1+x^{2})
\end{align}

　ここで\(\displaystyle{I_{1}=\int_{0}^{1}dx\,x^{2}\tan^{-1}x,\,I_{2}=\int_{0}^{1}dx\,x\log(1+x^{2})}\)として別々で計算する。まず\(I_{1}\)については、\(f(x)=\tan^{-1}x,\,g(x)=x^{3}/3\)として部分積分法を用いて

\begin{align}
I_{1}&=\int_{0}^{1}dx\,x^{2}\tan^{-1}x \notag \\
&=\left[\frac{1}{3}x^{3}\tan^{-1}x\right]_{0}^{1}-\frac{1}{3}\int_{0}^{1}dx\frac{x^{3}}{1+x^{2}} \notag \\
&=\frac{\pi}{12}-\frac{1}{3}\int_{0}^{1}dx\left(x-\frac{x}{1+x^{2}}\right) \notag \\
&=\frac{\pi}{12}-\frac{1}{3}\left[\frac{1}{2}x^{2}-\frac{1}{2}\log(1+x^{2})\right]_{0}^{1} \notag \\
&=\frac{\pi}{12}-\frac{1}{6}(1-\log2)
\end{align}

となる。続いて\(I_{2}\)については、\(f(x)=\log (1+x^{2}),\,g(x)=x^{2}/2\)として部分積分法を用いて

\begin{align}
I_{2}&=\int_{0}^{1}dx\,x\log(1+x^{2}) \notag \\
&=\left[\frac{1}{2}x^{2}\log (1+x^{2})\right]_{0}^{1}-\int_{0}^{1}dx\,\frac{1}{2}x^{2}\cdot\frac{2x}{1+x^{2}} \notag \\
&=\frac{1}{2}\log2-\int_{0}^{1}dx\frac{x^{3}}{1+x^{2}} \notag \\
&=\frac{1}{2}\log2-\frac{1}{2}(1-\log2) \notag \\
&=\log2-\frac{1}{2}
\end{align}

となる。途中\(I_{1}\)での計算結果を流用した。よって求めた\(I_{1},I_{2}\)を利用して

\begin{align}
\int_{0}^{1}dx\,\left\{x^{2}\tan^{-1}x-\frac{1}{2}x\log(1+x^{2})\right\}&=I_{1}-\frac{1}{2}I_{2} \notag \\
&=\frac{\pi}{12}-\frac{1}{6}(1-\log2)-\frac{1}{2}\left(\log2-\frac{1}{2}\right) \notag \\
&=\boxed{\frac{\pi}{12}-\frac{1}{3}\log2+\frac{1}{12}}
\end{align}

となる。

被積分関数が変数分離できない場合

解説

(1)

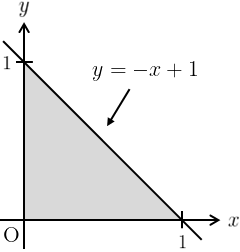
　積分領域は右図のようになり、求める積分は

\begin{align}
\int_{0}^{1}dx\int_{0}^{-x+1}dy\,(x^{2}+y^{2})
\end{align}

となる。

　まず\(y\)での積分が\(x\)に依存しているため、\(y\)での積分から実行する。

\begin{align}
&\int_{0}^{1}dx\int_{0}^{-x+1}dy\,(x^{2}+y^{2})\\
=&\int_{0}^{1}dx\left[x^{2}y+\frac{1}{3}y^{3}\right]_{0}^{-x+1} \notag \\
=&\int_{0}^{1}dx\left\{x^{2}(-x+1)+\frac{1}{3}(-x+1)^{3}\right\} \notag \\
=&-\frac{1}{3}\int_{0}^{1}dx\,(4x^{3}-6x^{2}+3x-1)
\end{align}

となる。

　次に\(x\)で積分する。

\begin{align}
-\frac{1}{3}\int_{0}^{1}dx\,(4x^{3}-6x^{2}+3x-1)&=-\frac{1}{3}\left[x^{4}-2x^{3}+\frac{3}{2}x^{2}-x\right]_{0}^{1} \notag \\
&=-\frac{1}{3}\left(1-2+\frac{3}{2}-1\right)=\boxed{\frac{1}{6}}
\end{align}

　

(2)

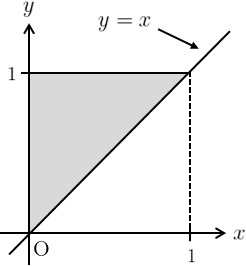
　積分領域は右図のようになり、求める積分は

\begin{align}
\int_{0}^{1}dy\int_{0}^{y}dx\,\sqrt{4y^{2}-x^{2}}
\end{align}

となる。

　まず\(x\)での積分が\(y\)に依存しているため、\(x\)での積分から実行する。\(x=2y\sin\theta\)として置換積分すると、\(\displaystyle{\frac{dx}{d\theta}=2y\cos\theta,\,0\leq\theta\leq\frac{\pi}{6}}\)より

\begin{align}
&\int_{0}^{1}dy\int_{0}^{y}dx\,\sqrt{4y^{2}-x^{2}}\\
=&\int_{0}^{1}dy\int_{0}^{\pi/6}2y\cos\theta d\theta\sqrt{4y^{2}-4y^{2}\sin^{2}\theta} \notag \\
=&\int_{0}^{1}dy\int_{0}^{\pi/6}d\theta\,4y^{2}\cos^{2}\theta
\end{align}

となり、積分領域が定数のみで決まり、被積分関数が変数分離可能なパターンに変形できる。よってそれぞれの変数で並行して積分できるようになり

\begin{align}
\int_{0}^{1}dy\int_{0}^{\pi/6}d\theta\,4y^{2}\cos^{2}\theta&=4\int_{0}^{1}dy\,y^{2}\int_{0}^{\pi/6}d\theta\,\frac{1}{2}(1+\cos2\theta) \notag \\
&=2\left[\frac{1}{3}y^{3}\right]_{0}^{1}\left[\theta+\frac{1}{2}\sin2\theta\right]_{0}^{\pi/6} \notag \\
&=2\cdot\frac{1}{3}\left(\frac{\pi}{6}+\frac{\sqrt{3}}{4}\right)=\boxed{\frac{\pi}{9}+\frac{\sqrt{3}}{6}}
\end{align}

となる。

　

　今回で逐次積分の問題演習を終了する。

　次回は変数変換を必要とする多重積分の問題を扱う。

　

　続きはこちら。