前回
からの続き。
クラスタリングの実装例の解説は終わっているが、最後にクラスタの数を決める指標になる「エルボー法」について書く。
エルボー法
エルボー法とは、クラスタの数に応じてSSEを計算してグラフ化し、その形状から最適と思われるクラスタの数を選択する手法である。
SSE(Sum of Squared errors of prediction)とは「クラスタ内誤差平方和」と呼ばれる量であり、イメージとしては各クラスタの重心から各点までの距離の総和と思っておけばよい。
例として、下図のグラフを示す。
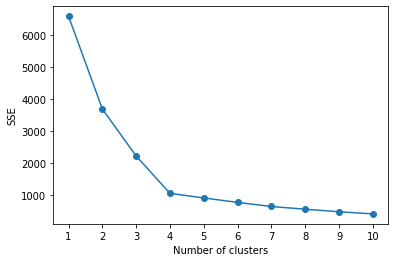
このグラフを見ながら、SSEとクラスタ数がともになるべく小さい組み合わせを見つける。
今回の例では、クラスタ数4のときがそれに該当すると言えそうだ。
さらによく見ると、クラスタ数が4のときにグラフの変化の仕方が急激に変わっていることがわかる。
このグラフの変化の仕方が大きく変わる部分が、腕を曲げた際の肘に似ていることから「エルボー法」という名前がついている。
実装例
実装例
# モジュールのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import sklearn
from sklearn.cluster import KMeans
# データセットのインポート
file=pd.read_csv('k-means.csv')
# データの割り振り
X=file.iloc[:,0:2]
# SSEの算出
SSE=[]
for i in range(1,11):
model = KMeans(n_clusters=i,
init='k-means++',
n_init=5,
max_iter=10,
random_state=0)
model.fit(X)
SSE.append(model.inertia_)
# グラフの描画
plt.plot(range(1,11), SSE, marker='o')
plt.xticks(np.arange(1,11,1))
plt.xlabel('Number of clusters')
plt.ylabel('SSE')
plt.show()出力例

実際にプログラムを実行したい場合は、下記ボタンよりcsvファイル「k-means.csv」をダウンロードしてプログラムの保存先に保存すること。
コード詳説
半分ほどは前回の流用なので、下記を参照。
# SSEの算出
SSE=[]
for i in range(1,11):
model = KMeans(n_clusters=i,
init='k-means++',
n_init=5,
max_iter=10,
random_state=0)
model.fit(X)
SSE.append(model.inertia_)⇒クラスタ数が1~10のときのSSEを計算し、その値を「SSE」という名前のリストに収納するコード。
最初に「SSE=[]」で、「SSE」という名の空のリストを作る。
次にクラスタ数がiのときのクラスタリングを実行し、そのときのSSEを「model.inertia_」で計算して「SSE.apend()」でリスト「SSE」に追加する。
このiを1~10まで変化させてそれぞれSSEを計算させ、順次その値をリスト「SSE」に格納していく。
# グラフの描画
plt.plot(range(1,11), SSE, marker='o')
plt.xticks(np.arange(1,11,1))
plt.xlabel('Number of clusters')
plt.ylabel('SSE')
plt.show()⇒縦軸をSSE、横軸をクラスタ数のグラフを描画するためのコード。
このコードによって下図のグラフが得られる。

終わりに
教師あり学習の分類問題も含めて、データをカテゴリーごとに分ける機械学習の代表格は大方抑えられたと思う。
しかし、教師なし学習にはもう1つ「次元削減」という代表的なアルゴリズムがある。
最後にこの次元削減を紹介して。教師なし学習の記事を締めようと思う。
参考文献
私が受講した通信講座。
機械学習とはなんぞやという体系的な話からPython操作の基礎、各アルゴリズムの理論、プログラムの実装例まで取り上げ、短期間で最低限の実用レベルまで学ぶことができるようになっている。
最低限の知識で全体を俯瞰しながら実装レベルまで学びたかった私にとって、最適な「足掛かり」となる講座だった。
END




コメント