【AI】機械学習 by Python：回帰分析編②～モジュールのインポート～

　前回

の続き。

　今回から、前回紹介した回帰分析の実装例のコード解説に入る。
　下記にもう一度、プログラムの実装例とその出力例を示しておく。

　

実装例

# モジュールのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import sklearn
from sklearn.linear_model import LinearRegression

# データセットのインポート
file=pd.read_csv('apartment.csv',encoding='cp932')
#データセットのサイズ確認
print('データセットのサイズ：',file.shape)

# 説明変数
X=file.iloc[:,1:]
# 目的変数
Y=file.iloc[:,0]

# 説明変数Xと目的変数を、学習データ（8割）とテストデータ（2割）に分割（random_stateは0）
X_train, X_test, Y_train, Y_test = sklearn.model_selection.train_test_split(X, Y, test_size=0.2, random_state=0)
# 分割の確認
print('分割の確認：',X_train.shape, X_test.shape, Y_train.shape, Y_test.shape)

# 回帰分析実行
# インスタンスの作成
model = LinearRegression()
# モデルの作成
model.fit(X_train, Y_train)

# 回帰直線の確認
# 切片
print('切片の値 = ', model.intercept_)
# 係数
print('係数の値 = ', model.coef_)

# 学習データからの予測値
pred_train = model.predict(X_train)
# テストデータからの予測値
pred_test = model.predict(X_test)

# 結果確認
print('学習データの平均二乗誤差： ', np.mean((Y_train - pred_train) ** 2))
print('テストデータの平均二乗誤差： ', np.mean((Y_test - pred_test) ** 2))
print('決定係数：',model.score(X_test,Y_test))

# モデルを使った計算
Xs=35 # 部屋の広さ[m^2]
Xt=10 # 駅から建物までの所要時間[min]
Xo=5 # 築年数[year]
price=model.intercept_+model.coef_[0]*Xs+model.coef_[1]*Xt+model.coef_[2]*Xo
print('部屋の広さ',Xs,'m^2、徒歩',Xt,'分、築',Xo,'年の建物の部屋の家賃は約',round(price,1),'万円である。')

　

出力例

データセットのサイズ： (100, 4)
分割の確認： (80, 3) (20, 3) (80,) (20,)
切片の値 =  7.506892589329363
係数の値 =  [ 0.15930654 -0.10031788 -0.14080724]
学習データの平均二乗誤差：  0.0006406930013219009
テストデータの平均二乗誤差：  0.0009590840329186921
決定係数： 0.999959366829125
部屋の広さ 35 m^2、徒歩 10 分、築 5 年の建物の部屋の家賃は約 11.4 万円である。

1. モジュールのインポート

　最初に書かれているのは、モジュールを読み込む(インポートする)ためのコードだ。

# モジュールのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import sklearn
from sklearn.linear_model import LinearRegression

　モジュールとは、端的に言うとプログラムが書かれたファイルのことである。

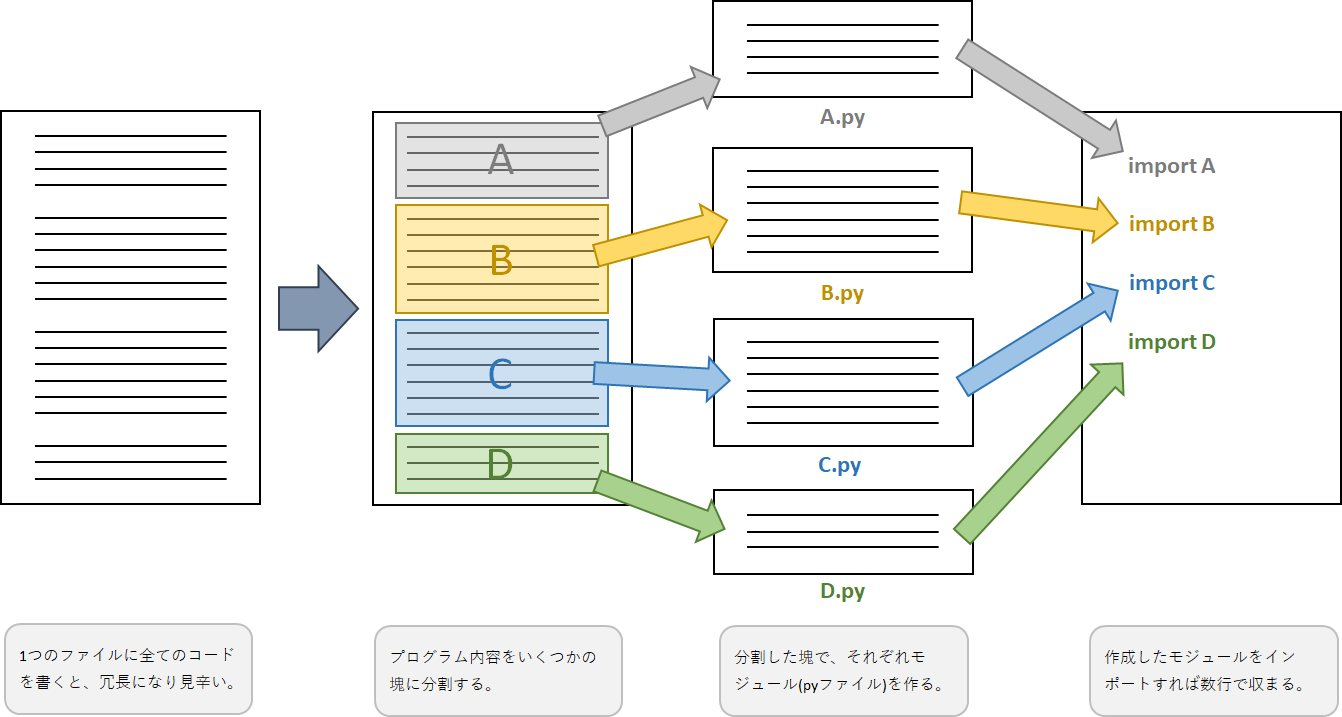
　前回少し述べたように、Pythonコードでプログラムが書かれたファイルにはいくつか種類があるが、ここでは拡張子が「.py」のPythonファイル(pyファイル)をモジュールと呼ぶことにする。

　Pythonでは、プログラムが書かれたpyファイルを別のファイルに読み込むことで、そのプログラムを実行することができる。
　これは、プログラムそのものが冗長になることを防ぎ、バグの発見にも役立つ。

　

　モジュールには大きく

・自作モジュール：自分が作ったモジュール。
・標準モジュール：Pythonに標準搭載されているモジュール。いわゆる組み込み関数。
・拡張モジュール：他言語で開発されたモジュール。いわゆるライブラリ。Anacondaインストールで使用可。

の3種類があり、今回の例でインポートしているのはすべて拡張モジュールだ。

　

　モジュールをインポートするコードは、例の上3行に書かれているように

である。

　○○にモジュール名が入り、△△にプログラム内でモジュールを使用する際の呼び出し名(大概は略名)が入る。
　この呼び出し名は自分で自由に決めてよい。

　

　また、あるモジュールから特定の関数だけをインポートしたい場合は、

を使う。

　○○にモジュール名、□□に関数名が入る。

　

　以上を踏まえて、例のコードを詳しく見ていくと次のようになる。

import numpy as np

⇒「NumPy」というライブラリをインポートし、「np」という名前で使うためのコード。
　「NumPy」はデータ分析に有効な関数を数多く揃えるライブラリである。

　

import pandas as pd　

⇒「pandas」というライブラリをインポートし、「pd」という名前で使うためのコード。
　「pandas」には大量のデータを効率よく扱うための関数が用意されている。

　

import matplotlib.pyplot as plt　
%matplotlib inline

⇒「matplotlib」というライブラリの「pyplot」というモジュールをインポートし、「plt」という名前で使うためのコード。
　「matplotlib」はグラフの描画に用いられるライブラリである。
　2行目の「%」以下はJupyter Notebook上に図表を表示させるためのコードである。

　

import sklearn
from sklearn.linear_model import LinearRegression

⇒　「scikit-learn」というライブラリをインポートし、その中にある「LinearRegression」というクラスをインポートするためのコード。
　「scikit-learn」は機械学習の手法を簡単に扱える関数が揃ったライブラリである。
　「LinearRegression」はその中でも、線形回帰モデルのクラスである。
　「クラス」とは今のところは仕様書(設計図)のようなものと認識しておけばよい。
　つまり「LinearRegression」は線形回帰モデルの仕様書(設計図)である。

次回予告

　モジュールのインポートだけでかなりの分量になったのでここで一旦区切る。

　次回は「データセットのインポート」から「説明変数と目的変数」まで一気に進める予定だ。

　

　END

　

　※追記
　データセットのインポートについて解説。