久々の力学。
3問目は運動のイメージがしやすい減衰振動を扱う。
問題
ばねは壁から垂直に立っており、ばね定数を\(k>0\)とする。
液体の粘性抗力係数を\(\mu>0\)とし、ばねはこの液体から速度\(v\)に比例する抵抗力\(-\mu v\)を受ける。
図の右向きを正として、自然長での球の位置を\(x=0\)する。
重力は考慮しなくてよい。
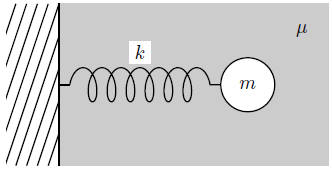
(1) ばねと液体から受ける力による球の運動は、時間\(t\)での球の位置を\(x(t)\)として、下記の形の微分方程式で記述できることを示せ。
\begin{align}
\frac{d^{2}x(t)}{dt^{2}}+2\gamma\frac{dx(t)}{dt}+\omega^{2}x(t)=0 \tag{Q1}\label{xhouteishiki}
\end{align}
(2) \(y(t)\)を実数値関数として複素数値関数\(z(t)=x(t)+iy(t)\)を定義する。この\(z(t)\)が
\begin{align}
\frac{d^{2}z(t)}{dt^{2}}+2\gamma\frac{dz(t)}{dt}+\omega^{2}z(t)=0 \tag{Q2}\label{zhouteishiki}
\end{align}
を満たすとき、\(x(t)\)が(\ref{xhouteishiki})を満たすことを示せ。
(3) \(\lambda\)を複素数として\(z(t)=e^{\lambda t}\)と置いたとき、\(z(t)\)が(\ref{zhouteishiki})を満たすなら
\begin{align}
\lambda=\begin{cases}
-\gamma\pm\sqrt{\gamma^{2}-\omega^{2}} &(\gamma>\omega) \\
-\gamma\pm i\sqrt{\omega^{2}-\gamma^{2}} &(\gamma<\omega)
\end{cases} \tag{Q3} \label{lambda}
\end{align}
となることを示せ。
(4)
(a) \(\gamma>\omega\)の条件下で\(x(t)\)を求めよ。ただし、\(t=0\)のとき球の位置を\(x(0)=x_{0}\)、速度を\(v(0)=dx(t)/dt|_{t=0}=v_{0}\)とする。
(b) 下記の場合について、それぞれ \(t=0\)以降の球の位置の時間変化を、 縦軸を変位\(x(t)\)、横軸を時間\(t\)のグラフで示せ。
(i) \(x_{0}=L>0, v_{0}=0\)
(ii) \(x_{0}=0, v_{0}=V>0\)
(5)
(a) \(\gamma<\omega\)の条件下で\(x(t)\)を求めよ。ただし、\(t=0\)のとき球の位置を\(x(0)=x_{0}\)、速度を\(v(0)=dx(t)/dt|_{t=0}=v_{0}\)とする。
(b) 下記の場合について、それぞれ \(t=0\)以降の球の位置の時間変化を、 縦軸を変位\(x(t)\)、横軸を時間\(t\)のグラフで示せ。
(i) \(x_{0}=L>0, v_{0}=0\)
(ii) \(x_{0}=0, v_{0}=V>0\)
解答(1)
重力は考慮しなくてよいため、球に加わる力は液体からの抵抗力とばねからの復元力の2つである。
よって運動方程式は
\begin{align}
m\frac{d^{2}x(t)}{dt^{2}}=-\mu\frac{dx(t)}{dt}-kx(t) \tag{1-1}\label{運動方程式1}
\end{align}
と書ける。
この(\ref{運動方程式1})を変形すれば、
\begin{align}
\frac{d^{2}x(t)}{dt^{2}}+2\gamma\frac{dx(t)}{dt}+\omega^{2}x(t)=0 \tag{1-2}\label{運動方程式2}
\end{align}
と書け、(\ref{xhouteishiki})と同じ形になる。ただし、\(\gamma=\mu/2m, \omega=\sqrt{k/m}\)である。
解答(2)
\(z(t)=x(t)+iy(t)\)を(\ref{zhouteishiki})に代入すると、
\begin{align}
\frac{d^{2}}{dt^{2}}\left\{ x(t)+iy(t) \right\}+2\gamma\frac{d}{dt}\left\{ x(t)+iy(t) \right\}+\omega^{2}\left\{ x(t)+iy(t) \right\}=0 \tag{2-2}\label{hosoku1-1}
\end{align}
となる。(\ref{hosoku1-1})を実部と虚部でわけて整理すると、
\begin{align}
\left\{\frac{d^{2}x(t)}{dt^{2}}+2\gamma\frac{dx(t)}{dt}+\omega^{2}x(t)\right\}+i\left\{\frac{d^{2}y(t)}{dt^{2}}+2\gamma\frac{dy(t)}{dt}+\omega^{2}y(t)\right\}=0 \tag{2-3}\label{hosoku1-2}
\end{align}
となる。(\ref{hosoku1-2})が成立するためには、実部と虚部がそれぞれ\(0\)でなければならないため、
\begin{gather}
\frac{d^{2}x(t)}{dt^{2}}+2\gamma\frac{dx(t)}{dt}+\omega^{2}x(t)=0 \tag{2-4}\label{hosoku1-3}\\
\frac{d^{2}y(t)}{dt^{2}}+2\gamma\frac{dy(t)}{dt}+\omega^{2}y(t)=0 \tag{2-5}\label{hosoku1-4}
\end{gather}
が成立する。(\ref{hosoku1-3})は(\ref{xhouteishiki})そのものである。
よって(\ref{zhouteishiki})を満たす\(z(t)\)が求まれば、\(z(t)\)の実部を取れば(\ref{xhouteishiki})を満たす\(x(t)\)を求められることがわかる。
解答(3)
複素数\(\lambda\)を用いて\(z(t)=e^{\lambda t}\)と置いたとき、\(dz(t)/dt=\lambda e^{\lambda t} , d^{2}z(t)/dt^{2}=\lambda^{2}e^{\lambda t}\)となるため、これを(\ref{zhouteishiki})に代入すると、
\begin{align}
\lambda^{2}e^{\lambda t}+2\gamma \lambda e^{\lambda t}+\omega^{2}e^{\lambda t}=0 \tag{3-1}\label{複素方程式2}
\end{align}
と書ける。さらにすべての項に\(e^{\lambda t}\)が含まれるため、
\begin{align}
\lambda^{2}+2\gamma \lambda+\omega^{2}=0 \tag{3-2}\label{複素方程式3}
\end{align}
と整理できる。
(\ref{複素方程式3})はお馴染みの二次方程式であるため、解の公式を使えば一発で
\begin{align}
\lambda=\begin{cases}
-\gamma\pm\sqrt{\gamma^{2}-\omega^{2}} &(\gamma>\omega) \\
-\gamma\pm i\sqrt{\omega^{2}-\gamma^{2}} &(\gamma<\omega)
\end{cases} \tag{3-3} \label{lambda2}
\end{align}
と解を求められる。
続きはこちら。





コメント