【力学】減衰振動②

　前回

の続き。

　今回から本格的に球の運動について考えていく。

解答(4)-(a)

　\(z(t)\)に関する微分方程式

\begin{align}
\frac{d^{2}z(t)}{dt^{2}}+2\gamma\frac{dz(t)}{dt}+\omega^{2}z(t)=0 \tag{Q2}\label{複素方程式1}
\end{align}

に\(z(t)=e^{\lambda t}\)を代入して得られた

\begin{align}
\lambda=\begin{cases}
-\gamma\pm\sqrt{\gamma^{2}-\omega^{2}} &(\gamma>\omega) \\
-\gamma\pm i\sqrt{\omega^{2}-\gamma^{2}} &(\gamma<\omega)
\end{cases} \tag{Q3} \label{sollambda}
\end{align}

の内、\(\gamma>\omega\)の場合の解を利用する。

　\(A,B\)を複素任意定数として、\(\gamma>\omega\)の場合の\(\lambda\)から得られる解の線形結合

\begin{align}
z(t)=Ae^{(-\gamma+\sqrt{\gamma^{2}-\omega^{2}})t}+Be^{(-\gamma-\sqrt{\gamma^{2}-\omega^{2}})t} \tag{4-1}\label{6ippan}
\end{align}

は(\ref{複素方程式1})の解であり、(\ref{複素方程式1})が二階の常微分方程式かつ(\ref{6ippan})に含まれる任意定数が2つであるため、(\ref{6ippan})は(\ref{複素方程式1})の一般解でもある。

　しかし\(\gamma>\omega\)のとき、根号の中身は正であるため\(\lambda\)は実数となる。
　その結果\(z(t)=e^{\lambda t}\)そのものが実数値関数になってしまうため、\(x(t)\)の一般解も結局(\ref{6ippan})と全く同じ形とる。
　よって任意定数を\(C_{1},D_{1}\)として、

\begin{align}
x(t)=C_{1}e^{(-\gamma+\sqrt{\gamma^{2}-\omega^{2}})t}+D_{1}e^{(-\gamma-\sqrt{\gamma^{2}-\omega^{2}})t} \tag{4-2}\label{gammadaiippan}
\end{align}

となる。

　ここで初期条件\(x(0)=x_{0}, dx(t)/dt|_{t=0}=v_{0}\)を利用して、任意定数を求めていく。
　(\ref{gammadaiippan})を利用すると、

\begin{align}
x(0)&=C_{1}e^{(-\gamma+\sqrt{\gamma^{2}-\omega^{2}})\cdot 0}+D_{1}e^{(-\gamma-\sqrt{\gamma^{2}-\omega^{2}})\cdot 0}\\
&=C_{1}+D_{1}=x_{0} \\
\left. \frac{dx(t)}{dt}\right|_{t=0}&=\left(-\gamma+\sqrt{\gamma^{2}-\omega^{2}}\right) C_{1}e^{(-\gamma+\sqrt{\gamma^{2}-\omega^{2}})\cdot -0}+ \left(-\gamma-\sqrt{\gamma^{2}-\omega^{2}}\right) D_{1}e^{(-\gamma-\sqrt{\gamma^{2}-\omega^{2}})\cdot 0} \\
&= \left(-\gamma+\sqrt{\gamma^{2}-\omega^{2}}\right) C_{1} + \left(-\gamma-\sqrt{\gamma^{2}-\omega^{2}}\right) D_{1}=v_{0}
\end{align}

すなわち

\begin{align}
&C_{1}+D_{1}=x_{0} \tag{4-3}\label{renritu1-1}\\
&\left(-\gamma+\sqrt{\gamma^{2}-\omega^{2}}\right) C_{1} + \left(-\gamma-\sqrt{\gamma^{2}-\omega^{2}}\right) D_{1}=v_{0} \tag{4-4}\label{renritu1-2}
\end{align}

となる。(\ref{renritu1-1})と(\ref{renritu1-2})を\(C_{1}, D_{1}\)について解けば、

\begin{align}
&C_{1}=\frac{(\gamma+\sqrt{\gamma^{2}-\omega^{2}})x_{0}+v_{0}}{2\sqrt{\gamma^{2}-\omega^{2}}} \tag{4-5}\label{C1} \\
&D_{1}=\frac{(-\gamma+\sqrt{\gamma^{2}-\omega^{2}})x_{0}-v_{0}}{2\sqrt{\gamma^{2}-\omega^{2}}} \tag{4-6}\label{D1}
\end{align}

となる。

　以上より、\(\gamma>\omega\)のとき\(x(t)\)は

\begin{align}
x(t)=\frac{(\gamma+ \alpha )x_{0}+v_{0}}{2 \alpha } e^{(-\gamma+ \alpha )t}+ \frac{(-\gamma+ \alpha )x_{0}-v_{0}}{2 \alpha } e^{(-\gamma- \alpha )t} \tag{4-7} \label{xgo}
\end{align}

となる。ただし\( \alpha =\sqrt{\gamma^{2}-\omega^{2}}\)と置いた。

解答(4)-(b)

　(i)のとき、すなわち\(x_{0}=L>0, v_{0}=0\)のとき、(\ref{xgo})は

\begin{align}
x(t)=\frac{(\gamma+ \alpha )L}{2 \alpha } e^{(-\gamma+ \alpha )t}+ \frac{(-\gamma+ \alpha )L}{2 \alpha } e^{(-\gamma- \alpha )t} \tag{4-8} \label{xgo1}
\end{align}

となる。

　(ii)のとき、すなわち\(x_{0}=0, v_{0}=V>0\)のとき、(\ref{xgo})は

\begin{align}
x(t)=\frac{V}{2 \alpha } \left\{e^{(-\gamma+ \alpha )t}-e^{(-\gamma- \alpha )t} \right\} \tag{4-9} \label{xgo2}
\end{align}

となる。

　これら(\ref{xgo1})と(\ref{xgo2})をグラフ化すると下図のようになる。

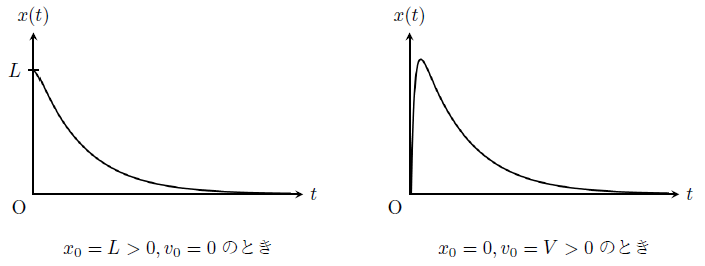
　(\ref{xgo1})は、球を\(x=L\)の位置まで引っ張ってきて、そこからそのまま(速度を与えず)手を離して運動させたときの変位の時間変化を表す。
　グラフを見ると、初期位置\(x(0)=L\)から時間をかけて自然長の位置まで戻っているのがわかる。
　よって\(\gamma>\omega\)のとき、球が浸っている液体はばねが振動できないほど粘性が大きいことがわかる。

　(\ref{xgo2})は、自然長の位置で球に速度\(V\)を与えて\(x>0\)の向きに運動させたときの変位の時間変化である。
　グラフを見ると、最初は右向きの速度を与えたことによって球が\(x>0\)の向きに運動するが、途中からばねに引き戻され、ゆっくりと自然長に戻っていることがわかる。

　

　続きはこちら。