にてアンペール・マクスウェルの法則、アンペールの法則、ビオ・サバールの法則を紹介した。
今回から、演習でよく取り上げられるビオ・サバールの法則とアンペールの法則の典型問題を解説していく。
まずは、ビオ・サバールの法則で解ける系から見ていく。
ビオ・サバールの法則
\begin{gather}
\vec{B}(\vec{r})=\frac{\mu_{0}I}{4\pi}\int_{C}\frac{d\vec{r}\,’\times(\vec{r}-\vec{r}\,’)}{|\vec{r}-\vec{r}\,’|^{3}} \label{bio1} \tag{1}
\end{gather}
無限長の直線電流が作る磁場
問題1
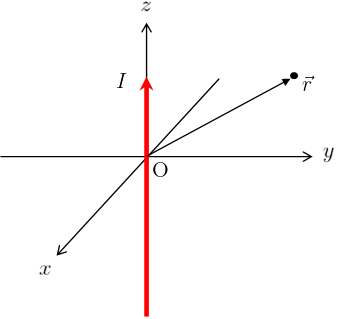
z軸上に太さを無視できる無限長の導線があり、その導線にz軸正の向きに定常電流\(I\)が流れている。
このとき、定常電流\(I\)が位置\(\vec{r}\)に作る磁場\(\vec{B}(\vec{r})\)を求めよ。
解説

本問題において、(\ref{bio1})に登場するパラメータを図示すると右図のようになる。
ここから
\begin{align}
&d\vec{r}\,’=(0,0,dz’) \label{drp}\tag{2}\\
&\vec{r}\,’=(0,0,z’) \label{rp}\tag{3}
\end{align}
となる。
よって(\ref{drp})と(\ref{rp})より
\begin{align}
&d\vec{r}\,’\times(\vec{r}-\vec{r}\,’)\\
=&(0,0,dz’)\times(x,y,z-z’)\\
=&(-ydz’,xdz’,0)\\
=&dz'(-y,x,0) \label{gaiseki1}\tag{4}
\end{align}
となるため、これを(\ref{bio1})に代入すると、
\begin{align}
\vec{B}(\vec{r})&=\frac{\mu_{0}I}{4\pi}\int_{C}\frac{d\vec{r}\,’\times(\vec{r}-\vec{r}\,’)}{|\vec{r}-\vec{r}\,’|^{3}}\\
&=\frac{\mu_{0}I}{4\pi}\int_{-\infty}^{\infty}\frac{dz'(-y,x,0)}{|\vec{r}-\vec{r}\,’|^{3}}\\
&=\frac{\mu_{0}I}{4\pi}\int_{-\infty}^{\infty}\frac{dz’}{|\vec{r}-\vec{r}\,’|^{3}}(-y,x,0) \label{linibio1}\tag{5}
\end{align}
となるため、後は定積分\(\displaystyle{\int_{-\infty}^{\infty}\frac{dz’}{|\vec{r}-\vec{r}\,’|^{3}}}\)を求めればよいが、そのままでは手が付けられないので次のように考える。
\(\vec{r}-\vec{r}\,’\)と\(d\vec{r}\,’\)がなす角度を\(\theta’\)とし、位置\(\vec{r}\)からz軸までの距離を\(r\)とすると図より
\begin{gather}
|\vec{r}-\vec{r}\,’|\sin\theta’=r\\
|\vec{r}-\vec{r}\,’|=\frac{r}{\sin\theta’} \label{r-rpoo1}\tag{6}
\end{gather}
となる。さらに図より、
\begin{gather}
\tan\theta’=\frac{r}{z-z’} \\
z’=z-\frac{r}{\tan\theta’} \label{tantheta}\tag{7}
\end{gather}
となるため、(\ref{tantheta})の両辺を\(\theta’\)で微分すると
\begin{align}
\frac{dz’}{d\theta’}=\frac{r}{\sin^{2}\theta’} \label{drdtheta}\tag{8}
\end{align}
となる。
よって、(\ref{r-rpoo1})と(\ref{drdtheta})を利用すると、
\begin{align}
\int_{-\infty}^{\infty}\frac{dz’}{|\vec{r}-\vec{r}\,’|^{3}}=\int_{0}^{\pi}\frac{\sin^{3}\theta’}{r^{3}}\cdot\frac{r}{\sin^{2}\theta’}d\theta’=\frac{1}{r^{2}}\int_{0}^{\pi}\sin\theta’d\theta’=\frac{2}{r^{2}} \label{sekibun1}\tag{9}
\end{align}
となるため、この(\ref{sekibun1})を(\ref{linibio1})に代入すると
\begin{align}
\vec{B}(\vec{r})=\frac{\mu_{0}I}{4\pi}\cdot\frac{2}{r^{2}}(-y,x,0)=\frac{\mu_{0}I}{2\pi r^{2}}(-y,x,0) \label{linibiokai1} \tag{10}
\end{align}
となる。
ここでさらに円筒座標系を導入すると、(\ref{linibiokai1})はさらに次のように書き換えられる。
\begin{align}
\vec{B}(\vec{r})=\frac{\mu_{0}I}{2\pi r^{2}}(-r\sin\theta,r\cos\theta,0) \qquad\therefore\boxed{\vec{B}(\vec{r})=\frac{\mu_{0}I}{2\pi r}(-\sin\theta,\cos\theta,0)}
\end{align}
この結果から、直線電流が作る磁場は大きさが\(\displaystyle{\frac{\mu_{0}I}{2\pi r}}\)であり、向きは電流の向きに対して右ねじの向きになることがわかる。
\(\displaystyle{H=\frac{B}{\mu_{0}}}\)を使えば、高校物理で直線電流が作る磁場の大きさとして暗記させられる関係式\(\displaystyle{H=\frac{I}{2\pi r}}\)が求められる。
また、この問題はアンペールの法則を用いても解くことができる。
詳細は下記を参照。
正方形電流が作る磁場
問題2
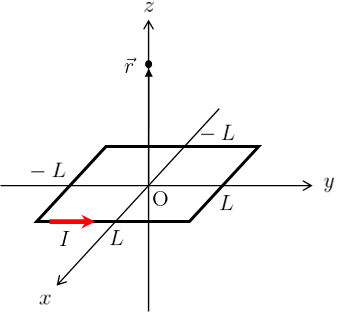
x-y平面上に一辺の長さが\(2L\)の正方形コイルが下図のように置かれ、z軸に対して右ねじの向きに定常電流\(I\)が流れている。
このとき、z軸上の点\(\vec{r}=(0,0,z)\)上に定常電流が作る磁場\(\vec{B}(\vec{r})\)を求めよ。
解説
各辺の名前を次のように命名する。
\begin{align}
&(-L,-L,0)-(L,-L,0)\,\to\,辺\text{a}\\
&(L,-L,0)-(L,L,0)\,\to\,辺\text{b}\\
&(L,L,0)-(-L,L,0)\,\to\,辺\text{c}\\
&(-L,L,0)-(-L,-L,0)\,\to\,辺\text{d}
\end{align}
正方形コイルの各辺が作る磁場をビオ・サバールの法則で求め、最後に求めた磁場をすべて足し上げればよい。
とはいえ、単純に全ての辺の寄与を求めるのは面倒なので、次のように考える。
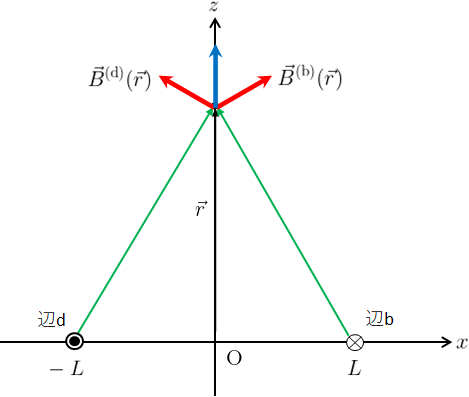
対辺同士が作る磁場は、対称性から図4のようにz軸方向以外の磁場は打ち消しあう。
また同様に対称性から、4つの辺がz軸上の同じ位置に作る磁場のz成分は、すべて同じ大きさになる。
よって、1辺が作る磁場のz成分のみを求めてそれを4倍すればよい。
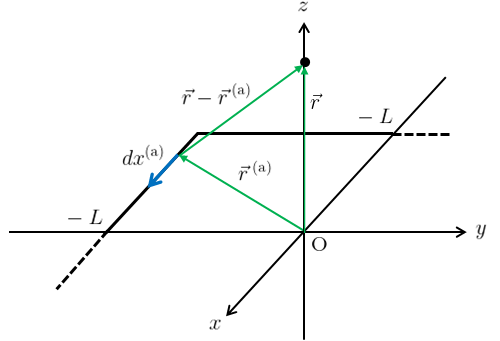
ここでは、辺aが作る磁場を4倍することにする。
辺aが作る磁場を\(\vec{B}^{\text{(a)}}(\vec{r})\)とすると(\ref{bio1})より
\begin{align}
\vec{B}^{\text{(a)}}(\vec{r})&=\frac{\mu_{0}I}{4\pi}\int_{\text{(a)}}\frac{d\vec{r}^{\text{(a)}}\times\{\vec{r}-\vec{r}^{\text{(a)}}\}}{|\vec{r}-\vec{r}^{\text{(a)}}|^{3}} \label{ba}\tag{11}
\end{align}
であり、積分の中身は
\begin{align}
d\vec{r}^{\text{(a)}}\times\{\vec{r}-\vec{r}^{\text{(a)}}\}&=(dx^{\text{(a)}},0,0)\times\{(0,0,z)-(x^{\text{(a)}},-L,0)\}\\
&=(dx^{\text{(a)}},0,0)\times(-x^{\text{(a)}},L,z)\\
&=(0,-zdx^{\text{(a)}},Ldx^{\text{(a)}}) \label{banakami}\tag{12}
\end{align}
となるため、\(\vec{B}^{\text{(a)}}(\vec{r})\)のz成分\(B_{z}^{\text{(a)}}(\vec{r})\)は
\begin{align}
B_{z}^{\text{(a)}}(\vec{r})=\frac{\mu_{0}I}{4\pi}\int_{-L}^{L}\frac{Ldx^{\text{(a)}}}{|\vec{r}-\vec{r}^{\text{(a)}}|^{3}}=\frac{\mu_{0}IL}{4\pi}\int_{-L}^{L}\frac{dx^{\text{(a)}}}{|\vec{r}-\vec{r}^{\text{(a)}}|^{3}} \label{bza}\tag{13}
\end{align}
となる。
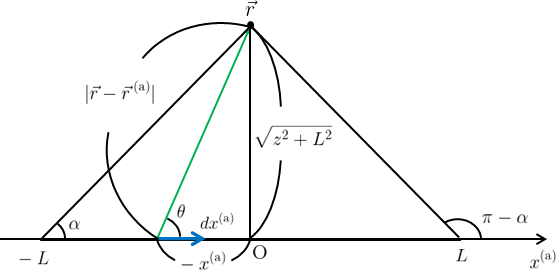
よって後は定積分\(\displaystyle{\int_{-L}^{L}\frac{dx^{\text{(a)}}}{|\vec{r}-\vec{r}^{\text{(a)}}|^{3}}}\)を求めればよい。
求め方は先の無限長の直線電流とほぼ同じだが、今回は長さが有限長であることに注意が必要である。
図6のように設定し、\(x^{\text{(a)}}\)の積分を\(\theta\)の積分に置換する。
このとき、
\begin{gather}
|\vec{r}-\vec{r}^{\text{(a)}}|\sin\theta=\sqrt{z^{2}+L^{2}}\\
|\vec{r}-\vec{r}^{\text{(a)}}|=\frac{\sqrt{z^{2}+L^{2}}}{\sin\theta} \label{yugenookisa}\tag{14}
\end{gather}
であり、
\begin{gather}
\tan{\theta}=\frac{\sqrt{z^{2}+L^{2}}}{-x^{\text{(a)}}}\\
x^{\text{(a)}}=-\frac{\sqrt{z^{2}+L^{2}}}{\tan\theta}\\
\frac{dx^{\text{(a)}}}{d\theta}=\frac{\sqrt{z^{2}+L^{2}}}{\sin^{2}\theta}\\
dx^{\text{(a)}}=\frac{\sqrt{z^{2}+L^{2}}}{\sin^{2}\theta}d\theta \label{dxadtheta}\tag{15}
\end{gather}
となるため、この(\ref{yugenookisa})と(\ref{dxadtheta})を(\ref{bza})に代入すると、
\begin{align}
B_{z}^{\text{(a)}}(\vec{r})&=\frac{\mu_{0}IL}{4\pi}\int_{\alpha}^{\pi-\alpha}\frac{\sin^{3}\theta}{(z^{2}+L^{2})^{\frac{3}{2}}}\cdot\frac{\sqrt{z^{2}+L^{2}}}{\sin^{2}\theta}d\theta\\
&=\frac{\mu_{0}IL}{4\pi(z^{2}+L^{2})}\int_{\alpha}^{\pi-\alpha}\sin\theta\,d\theta\\
&=\frac{\mu_{0}IL}{4\pi(z^{2}+L^{2})}\cdot 2\cos\alpha\\
&=\frac{\mu_{0}IL}{2\pi(z^{2}+L^{2})}\cdot\frac{L}{\sqrt{z^{2}+2L^{2}}}\\
&=\frac{\mu_{0}IL^{2}}{2\pi(z^{2}+L^{2})\sqrt{z^{2}+2L^{2}}} \label{bzaans}\tag{16}
\end{align}
と求められる。
以上より、後は(\ref{bzaans})を4倍すればよいため求める磁場は
\begin{gather}
\vec{B}(\vec{r})=(0,0,4B_{z}^{\text{(a)}}(\vec{r}))=\frac{2\mu_{0}IL^{2}}{\pi(z^{2}+L^{2})\sqrt{z^{2}+2L^{2}}}(0,0,1)\\
\therefore\boxed{\vec{B}(\vec{r})=\frac{2\mu_{0}IL^{2}}{\pi(z^{2}+L^{2})\sqrt{z^{2}+2L^{2}}}(0,0,1)}
\end{gather}
となる。
長くなるのでここで一旦区切る。
次回は円形電流とソレノイドが作る磁場をビオ・サバールの法則で求めていく。
続きはこちら。




コメント