【力学】2質点の連成振動～行列の力～②

　下記の続き。

　今回から本格的に、各球の運動を調べていく。

解答(3)

　ここで、$\vec{y}(t)=\mathsf{O}^{\text{T}}\vec{x}(t)$を満たすベクトル$\vec{y}(t) =(y_{\text{a}}(t), y_{\text{b}}(t) ) ^{\text{T}}$を導入する。 このとき、

$$\begin{align} \frac{d^{2}}{dt^{2}}\vec{y}(t)&=\frac{d^{2}}{dt^{2}}\mathsf{O}^{\text{T}}\vec{x}(t)=\mathsf{O}^{\text{T}}\frac{d^{2}}{dt^{2}}\vec{x}(t)=\mathsf{O}^{\text{T}}\left\{-\frac{k}{m}\,\mathsf{A}\,\vec{x}(t)\right\}=-\frac{k}{m}\, \mathsf{O}^{\text{T}}\mathsf{A}\,\vec{x}(t) \\ &=-\frac{k}{m}\, \mathsf{O}^{\text{T}}\mathsf{O}\Lambda\mathsf{O}^{\text{T}}\,\vec{x}(t)=-\frac{k}{m}\,\Lambda\mathsf{O}^{\text{T}}\,\vec{x}(t)=-\frac{k}{m}\,\Lambda\,\vec{y}(t) \end{align}$$

すなわち

$$\begin{align} \frac{d^{2}}{dt^{2}}\vec{y}(t)=-\frac{k}{m}\begin{pmatrix}1&0\\0&3\end{pmatrix}\vec{y}(t)\quad\Longrightarrow\quad\begin{cases} \displaystyle{\frac{d^{2}}{dt^{2}}y_{\text{a}}(t)=-\frac{k}{m}y_{\text{a}}(t)} \\ \displaystyle{\frac{d^{2}}{dt^{2}}y_{\text{b}}(t)=-\frac{3k}{m}y_{\text{b}}(t) } \end{cases} \tag{3-1}\label{ybibun} \end{align}$$

が成立する。

　この2つの微分方程式($\ref{ybibun}$)をそれぞれ解くと、一般解は

$$\begin{align} \begin{cases} y_{\text{a}}(t)=C_{\text{a}}\cos(\omega t+\phi_{\text{a}}) \\ y_{\text{b}}(t)=C_{\text{b}}\cos\left(\sqrt{3}\,\omega t+\phi_{\text{b}}\right) \end{cases} \tag{3-2}\label{yippan} \end{align}$$

となる。ただし$\omega=\sqrt{k/m}$、$C_{\text{a}}, C_{\text{b}} , \phi_{\text{a}} , \phi_{\text{b}}$は任意定数である。

　もともと$\vec{y}(t)=\mathsf{O}^{\text{T}}\vec{x}(t)$と定義していたため、

$$\begin{align} \vec{x}(t)=\mathsf{O}\,\vec{y}(t)=\frac{1}{\sqrt{2}}\begin{pmatrix}1 & -1\\1 &1\end{pmatrix}\begin{pmatrix} C_{\text{a}}\cos(\omega t+\phi_{\text{a}}) \\ C_{\text{b}}\cos\left(\sqrt{3}\,\omega t+\phi_{\text{b}}\right) \end{pmatrix} \end{align}$$

すなわち

$$\begin{align} \begin{cases} \displaystyle{x_{\text{a}}(t)=\frac{1}{\sqrt{2}}\left\{ C_{\text{a}}\cos(\omega t+\phi_{\text{a}})- C_{\text{b}}\cos\left(\sqrt{3}\,\omega t+\phi_{\text{b}}\right) \right\}}\\ \displaystyle{x_{\text{b}}(t)=\frac{1}{\sqrt{2}}\left\{ C_{\text{a}}\cos(\omega t+\phi_{\text{a}})+ C_{\text{b}}\cos\left(\sqrt{3}\,\omega t+\phi_{\text{b}}\right) \right\}} \end{cases}\tag{3-3}\label{aippan} \end{align}$$

と求められる。

　

　ここで初期条件を代入し、各任意定数を決定していく。

　(i)のとき、

$$\begin{align} &x_{\text{a}}(0)=\frac{1}{\sqrt{2}}\left\{ C_{\text{a}}\cos\phi_{\text{a}}- C_{\text{b}}\cos\phi_{\text{b}} \right\}=L \\ &\left.\frac{dx_{\text{a}}(t)}{dt}\right|_{t=0}=-\frac{\omega}{\sqrt{2}}\left\{ C_{\text{a}}\sin\phi_{\text{a}}- \sqrt{3}\,C_{\text{b}}\sin\phi_{\text{b}}\right\}=0\\ &x_{\text{b}}(0)=\frac{1}{\sqrt{2}}\left\{ C_{\text{a}}\cos\phi_{\text{a}}+C_{\text{b}}\cos\phi_{\text{b}} \right\}=L\\ &\left.\frac{dx_{\text{b}}(t)}{dt}\right|_{t=0}=-\frac{\omega}{\sqrt{2}}\left\{ C_{\text{a}}\sin\phi_{\text{a}}+ \sqrt{3}\, C_{\text{b}}\sin\phi_{\text{b}}\right\}=0 \end{align}$$

すなわち

$$\begin{align} &C_{\text{a}}\cos\phi_{\text{a}}- C_{\text{b}}\cos\phi_{\text{b}}=\sqrt{2}\,L \tag{3-4}\label{ixa0} \\ &C_{\text{a}}\sin\phi_{\text{a}}- \sqrt{3}\, C_{\text{b}}\sin\phi_{\text{b}}=0 \tag{3-5}\label{iva0} \\ &C_{\text{a}}\cos\phi_{\text{a}}+C_{\text{b}}\cos\phi_{\text{b}}=\sqrt{2}\,L \tag{3-6}\label{ixb0} \\ &C_{\text{a}}\sin\phi_{\text{a}}+ \sqrt{3}\, C_{\text{b}}\sin\phi_{\text{b}}=0 \tag{3-7}\label{ivb0} \end{align}$$

　これら($\ref{ixa0}$)～($\ref{ivb0}$)を$C_{\text{a}}, C_{\text{b}} , \phi_{\text{a}} , \phi_{\text{b}}$の連立方程式として解くと、$C_{\text{a}}=\sqrt{2}\,L,\,C_{\text{b}}=0,\,\phi_{\text{a}}=0$となる。($C_{\text{b}}=0$より$\phi_{\text{b}}$は考えなくてよい。)

　よってこれらを代入すると、

$$\begin{align} \begin{cases} x_{\text{a}}(t)=L\cos(\omega t) \\ x_{\text{b}}(t)=L\cos(\omega t) \end{cases}\tag{3-8}\label{ikai} \end{align}$$

となる。

　続いて(ii)のとき、

$$\begin{align} &x_{\text{a}}(0)=\frac{1}{\sqrt{2}}\left\{ C_{\text{a}}\cos\phi_{\text{a}}- C_{\text{b}}\cos\phi_{\text{b}} \right\}=0 \\ &\left.\frac{dx_{\text{a}}(t)}{dt}\right|_{t=0}=-\frac{\omega}{\sqrt{2}}\left\{ C_{\text{a}}\sin\phi_{\text{a}}- \sqrt{3}\,C_{\text{b}}\sin\phi_{\text{b}}\right\}=V\\ &x_{\text{b}}(0)=\frac{1}{\sqrt{2}}\left\{ C_{\text{a}}\cos\phi_{\text{a}}+C_{\text{b}}\cos\phi_{\text{b}} \right\}=0\\ &\left.\frac{dx_{\text{b}}(t)}{dt}\right|_{t=0}=-\frac{\omega}{\sqrt{2}}\left\{ C_{\text{a}}\sin\phi_{\text{a}}+ \sqrt{3}\, C_{\text{b}}\sin\phi_{\text{b}}\right\}=0 \end{align}$$

すなわち

$$\begin{align} &C_{\text{a}}\cos\phi_{\text{a}}- C_{\text{b}}\cos\phi_{\text{b}}=0 \tag{3-9}\label{iixa0} \\ &C_{\text{a}}\sin\phi_{\text{a}}- \sqrt{3}\, C_{\text{b}}\sin\phi_{\text{b}}=-\frac{\sqrt{2}\,V}{\omega} \tag{3-10}\label{iiva0} \\ &C_{\text{a}}\cos\phi_{\text{a}}+C_{\text{b}}\cos\phi_{\text{b}}=0 \tag{3-11}\label{iixb0} \\ &C_{\text{a}}\sin\phi_{\text{a}}+ \sqrt{3}\, C_{\text{b}}\sin\phi_{\text{b}}=0 \tag{3-12}\label{iivb0} \end{align}$$

　これら($\ref{iixa0}$)～($\ref{iivb0}$)を$C_{\text{a}}, C_{\text{b}} , \phi_{\text{a}} , \phi_{\text{b}}$の連立方程式として解くと、$C_{\text{a}}=V/(\sqrt{2}\,\omega),\,$$C_{\text{b}}=-V/(\sqrt{6}\,\omega),\,\phi_{\text{a}}=\phi_{\text{b}}=-\pi/2$となる。

　よってこれらを代入すると、

$$\begin{align} \begin{cases} \displaystyle{x_{\text{a}}(t)=\frac{V}{2\,\omega}\left\{\cos\left(\omega t-\frac{\pi}{2}\right)+\frac{1}{\sqrt{3}}\cos\left(\sqrt{3}\,\omega t-\frac{\pi}{2}\right) \right\}}\\ \displaystyle{x_{\text{a}}(t)=\frac{V}{2\,\omega}\left\{\cos\left(\omega t-\frac{\pi}{2}\right)-\frac{1}{\sqrt{3}}\cos\left(\sqrt{3}\,\omega t-\frac{\pi}{2}\right) \right\}} \end{cases}\tag{3-13}\label{iikai} \end{align}$$

となる。

　

　以上をまとめると

となる。

　

　ここで、(i)、(ii)それぞれの運動について考える。

　(i)は下図のように、2つの球ともに右側に長さ$L$だけ移動させてから、手を離して運動させることに相当する。

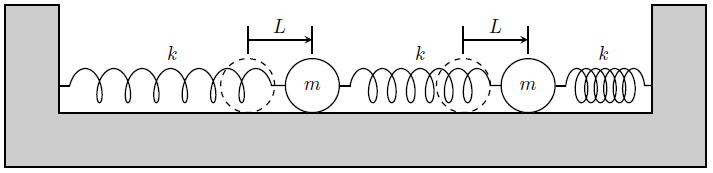
　この場合、2つの球とその間のばねが一体となって単振動すると予想できる。
　そして実際に計算するとその予想通り、$x_{\text{a}}(t)=x_{\text{b}}(t)=L\cos(\sqrt{k/m}\,t)$となり、2つの球がともに振幅$L$の単振動をすることがわかる。

　続いて(ii)だが、これは球aにのみ初速度$V>0$を与えて運動させる場合に相当する。
　得られた$x_{\text{a}}(t) , x_{\text{b}}(t)$をグラフにすると下図のようになる。

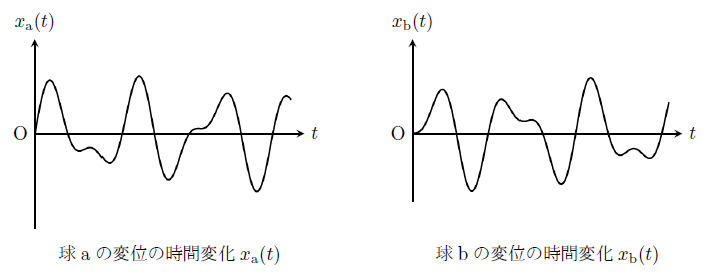
　(ii)では球aのみに初速度を与えるため、球aと球bで異なる運動をする。
　予想では、両者が全く予測がつかない不規則な振動をするように思える。
　しかし実際は、一見数式化できないように思える運動でも数式で表現できてしまい、時間変化を把握することができる。

終わりに

　今回は2つの球の連成振動を扱った。

　だが今回の問題を見てもらうとわかるように、問題設定が変わっても基本的な解き方は変わらない。

　運動方程式を行列で書き直し、対角化し、単振動の運動方程式の形に落とし込み、微分方程式を解く。
　球の数が増えようが、その質量が変わろうが、ばね定数が変わろうが、連成振動はこの解き方で運動を記述できる。

　これも行列の強みである。

　次回は別のさらに便利な道具を導入し、今回より少し複雑な系の問題を考えようと思う。

　

　END