【解析力学】オイラー・ラグランジュ方程式①

　大学で物理を専攻すると、古典力学(高校物理で言う力学)の後に解析力学を履修することになるだろう。

　解析力学とは簡単に言えば「古典力学の問題の解き方を画一化して機械的に解くことを目指す学問」である。
　力学に登場する種々の問題(落下、衝突、ばね振り子といったあらゆる問題)を、すべて1つの方法で楽に解いてしまおうというわけだ。

　そして、その解析力学の初歩として登場するのがオイラー・ラグランジュ方程式だ。

　本記事では、そのオイラー・ラグランジュ方程式を導入し、その利用例を簡単に見ていきたい。

導入

　今回は簡単のため、一次元系での運動のみを考える。

　系の全運動エネルギーを\(T\)、全ポテンシャルエネルギーを\(U\)として、ラグランジアン\(L\)という量を次式で定義する。

\begin{align}
L=T-U \tag{1}\label{lagteigi}
\end{align}

　このとき、ある物体の位置を\(x_{i}\)、速度を\(v_{i}\)とすると、オイラー・ラグランジュ方程式は

\begin{align}
\frac{d}{dt}\left(\frac{\partial L}{\partial v_{i}}\right)-\frac{\partial L}{\partial x_{i}}=0 \tag{2}\label{elteigi}
\end{align}

と書ける。

　このオイラー・ラグランジュ方程式は運動方程式と等価である。

例

　前回取り上げた、2質点の連成振動を考えよう。

　この系では、下図のように質量\(m\)の2つの球がばね定数\(k>0\)のばねに繋がれ、ばねの両端は壁に取り付けられている。

　

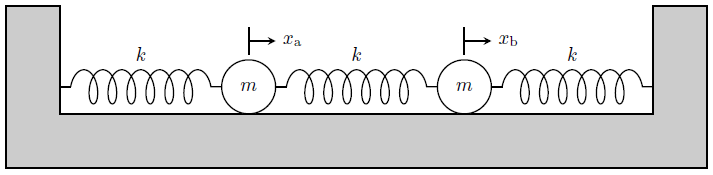
　この系の運動方程式を、オイラー・ラグランジュ方程式を使って導く。

　まず、系の全運動エネルギー\(T\)は、球aと球bの速度をそれぞれ\(v_{\text{a}},v_{\text{b}}\)として

\begin{align}
T=\frac{1}{2}mv_{\text{a}}^{2}+\frac{1}{2}mv_{\text{b}}^{2} \tag{3}\label{expt}
\end{align}

となる。
　続いて系の全ポテンシャルエネルギーは\(U\)は、3つのばねの弾性エネルギーを考えればよいため、球aと球bの変位をそれぞれ\(x_{\text{a}},x_{\text{b}}\)として

\begin{align}
U=\frac{1}{2}kx_{\text{a}}^{2}+ \frac{1}{2}k(x_{\text{a}}- x_{\text{b}})^{2} + \frac{1}{2}kx_{\text{b}}^{2} \tag{4}\label{expu}
\end{align}

と書ける。

　以上より、ラグランジアン\(L\)は(\ref{lagteigi})、(\ref{expt})、(\ref{expu})より

\begin{align}
L=\frac{1}{2}mv_{\text{a}}^{2}+\frac{1}{2}mv_{\text{b}}^{2}-\frac{1}{2}kx_{\text{a}}^{2}-\frac{1}{2}k(x_{\text{a}}- x_{\text{b}})^{2}-\frac{1}{2}kx_{\text{b}}^{2} \tag{5}\label{expl}
\end{align}

となる。

　

　続いて、上で求めた(\ref{expl})を(\ref{elteigi})に代入して運動方程式を求める。

　まずは球aについて考えると、

\begin{align}
&\frac{d}{dt}\left(\frac{\partial L}{\partial v_{\text{a}}}\right)=\frac{d}{dt}\left\{\frac{\partial}{\partial v_{\text{a}}}\left(\frac{1}{2}mv_{\text{a}}^{2}\right)\right\}=\frac{d}{dt}mv_{\text{a}}=m\frac{d^{2} x_{\text{a}} }{dt^{2}} \\
&\frac{\partial L}{\partial x_{\text{a}}}=\frac{\partial}{\partial x_{\text{a}}}\left\{ -\frac{1}{2}kx_{\text{a}}^{2}-\frac{1}{2}k(x_{\text{a}} – x_{\text{b}})^{2} \right\}=-kx_{\text{a}}-k (x_{\text{a}} – x_{\text{b}})
\end{align}

であるため、オイラー・ラグランジュ方程式は

\begin{gather}
\frac{d}{dt}\left(\frac{\partial L}{\partial v_{\text{a}}}\right)-\frac{\partial L}{\partial x_{\text{a}}}=0 \\
m\frac{d^{2} x_{\text{a}} }{dt^{2}}-\left\{ -kx_{\text{a}}-k (x_{\text{a}} – x_{\text{b}}) \right\}=0 \\
\boxed{m\frac{d^{2} x_{\text{a}} }{dt^{2}}=-kx_{\text{a}}-k (x_{\text{a}} – x_{\text{b}})} \tag{6}\label{aeq}
\end{gather}

となる。

　続いて球bについて考えると

\begin{align}
&\frac{d}{dt}\left(\frac{\partial L}{\partial v_{\text{b}}}\right)=\frac{d}{dt}\left\{\frac{\partial}{\partial v_{\text{b}}}\left(\frac{1}{2}mv_{\text{b}}^{2}\right)\right\}=\frac{d}{dt}mv_{\text{b}}=m\frac{d^{2} x_{\text{b}} }{dt^{2}} \\
&\frac{\partial L}{\partial x_{\text{b}}}=\frac{\partial}{\partial x_{\text{b}}}\left\{-\frac{1}{2}k(x_{\text{a}}- x_{\text{b}})^{2}-\frac{1}{2}kx_{\text{b}}^{2}\right\}=k (x_{\text{a}} – x_{\text{b}}) -kx_{\text{b}}
\end{align}

であるため、オイラー・ラグランジュ方程式は

\begin{gather}
\frac{d}{dt}\left(\frac{\partial L}{\partial v_{\text{b}}}\right)-\frac{\partial L}{\partial x_{\text{b}}}=0 \\
m\frac{d^{2} x_{\text{b}} }{dt^{2}}-\left\{ k (x_{\text{a}} – x_{\text{b}}) -kx_{\text{b}} \right\}=0 \\
\boxed{m\frac{d^{2} x_{\text{b}} }{dt^{2}}= k (x_{\text{a}} – x_{\text{b}}) -kx_{\text{b}} } \tag{7}\label{beq}
\end{gather}

となる。

　これら(\ref{aeq})と(\ref{beq})はそれぞれ、球aと球bに関する運動方程式である。

感動

　私が初めてオイラー・ラグランジュ方程式の使い方を知ったとき、最初に覚えたのは感動だった。

　恥ずかしい話、ばねの両端に質点がある問題で運動方程式を立てるときに、私は弾性力の符号を決めるのに時間がかかる。

　上記のような思考実験を問題の度に繰り返すのは、正直言って面倒くさかった。

　

　しかし、オイラー・ラグランジュ方程式を使えば上記のような思考実験は一切不要だ。

　やることは
　①全運動エネルギーから全ばねの弾性エネルギーを引いたラグランジアンを導入。
　②ラグランジアンを変位と速度で偏微分する。
　という機械的な計算だけ。

　これだけで運動方程式を求められてしまうのだ。

　微分方程式と行列の強力さを知ったときも驚いたが、まだまだ便利で強力な武器が存在することを知り、より物理を面白く感じたのを覚えている。

終わりに

　表題では①としているが、一旦ここで区切りをつける。

　①としたのは、オイラー・ラグランジュ方程式のもう1つのスゴさを紹介しきれていないからだ。
　だがここで紹介すると長くなるので次回以降に持ち越す。

　まずは今回導入したオイラー・ラグランジュ方程式を使って、1次元系のさまざまな力学の問題を解いていこうと思う。

　

　END