今まではは質点が1つの系しか扱ってこなかったが、今回は初めて質点が複数存在する系を扱う。
高校物理では、複数の質点を相手にするのは衝突の問題(運動量保存、反発係数)ぐらいしかない。
しかも、互いが同時に運動に関与するのは衝突する一瞬だけであり、その前後は今までの1つの質点による運動と同じである。
しかし、大学では複数の質点が時間的に連続して互いに互いの運動に関与する問題を扱う。
その際に力を発揮するのが行列である。
今回は、その行列が威力を発揮する良い例として2質点の連成振動を扱う。
問題
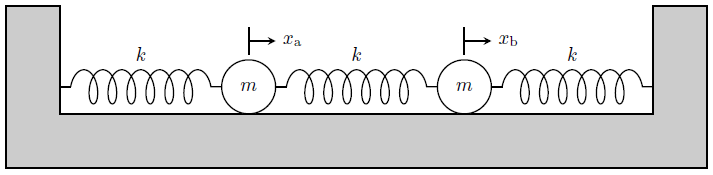
下図のように、質量\(m\)の2つの球が自然長の3つのばねにつながれ、両端のばねが壁に取り付けられている。
それぞれ自然長の位置を基準に、図の左側の球の変位を\(x_{\text{a}}\)、右側の球の変位を\(x_{ \text{b} }\)とする。
2つの球は質点とし、3つのばねのばね定数はすべて\(k>0\)とする。
また、重力、空気抵抗、床との摩擦は考慮しなくてよい。
(1) 各球に関する運動方程式を立てよ。
(2) \(\vec{x}(t) =(x_{\text{a}}(t), x_{\text{b}}(t) ) ^{\text{T}} \)と置き、(1)で求めた2つの運動方程式を
\begin{align}
m\frac{d^{2}}{dt^{2}}\vec{x}(t)=-k\,\mathsf{A}\,\vec{x}(t) \tag{Q1}\label{Aundou}
\end{align}
の形にまとめ、行列\(\mathsf{A}\)を対角化せよ。
(3) 初期条件が下記のとき、2つの球の変位の時間変化\(x_{ \text{a} }(t), x_{ \text{b} }(t)\)をそれぞれ求めよ。
(i) \(x_{ \text{a}}(0)=x_{ \text{b}}(0)=L>0,\quad\displaystyle{\left.\frac{dx_{\text{a}}(t)}{dt}\right|_{t=0}= \left.\frac{dx_{\text{b}}(t)}{dt}\right|_{t=0}=0}\)
(ii) \(x_{ \text{a}}(0)=x_{ \text{b}}(0)=0, \quad\displaystyle{\left.\frac{dx_{\text{a}}(t)}{dt}\right|_{t=0}}=V>0,\quad\displaystyle{\left.\frac{dx_{\text{b}}(t)}{dt}\right|_{t=0}}=0\)
解答(1)
まずは、各球の運動方程式を立てる。
球a、球bともに両隣のばねから受ける力のみを考えればよい。
球aに関しては、左側のばねからは球aの変位のみの影響を受けて\(-kx_{\text{a}}\)の力を、右側のばねからは球aと球bの両方の変位を考慮して \(-k(x_{\text{a}}- x_{\text{b}} )\)の力を受ける。
よって球aに関する運動方程式は
\begin{align}
m\frac{d^{2}x_{\text{a}}(t)}{dt^{2}}=-kx_{\text{a}}(t)-k\{x_{\text{a}}(t)- x_{\text{b}}(t)\} \tag{1-1}\label{aundou1}
\end{align}
と書ける。
球b関しては、左側のばねからは球aと球bの両方の変位を考慮して\(-k(x_{\text{b}}-x_{\text{a}})\)の力を、右側のばねからは球bの変位のみの影響を受けて\(-kx_{\text{b}}\)の力を受ける。
よって球bに関する運動方程式は
\begin{align}
m\frac{d^{2}x_{\text{b}}(t)}{dt^{2}}=-k\{x_{\text{b}} (t) -x_{\text{a}} (t) \}-kx_{\text{b}} (t) \tag{1-2}\label{bundou1}
\end{align}
と書ける。
以上をまとめると、
\begin{gather}
\begin{cases}
\displaystyle{m\frac{d^{2}x_{\text{a}}(t)}{dt^{2}}=-k\{2x_{\text{a}}(t)-x_{\text{b}}(t)}\} \\
\displaystyle{m\frac{d^{2}x_{\text{b}}(t)}{dt^{2}}=-k\{-x_{\text{a}}(t)+2kx_{\text{b}}(t)}\}
\end{cases} \tag{1-3}\label{undoumatome}
\end{gather}
となる。
解答(2)
\(\vec{x}(t) =(x_{\text{a}}(t), x_{\text{b}}(t) ) ^{\text{T}} \)と置くと(\ref{undoumatome})は
\begin{align}
m\frac{d^{2}}{dt^{2}}\vec{x}(t)=-k\begin{pmatrix}2 & -1 \\ -1 & 2\end{pmatrix}\vec{x}(t)=-k\,\mathsf{A}\,\vec{x}(t) \tag{2-1}\label{matateigi}
\end{align}
と書き直せる。
この行列\(\mathsf{A}\)を対角化する。
\(\mathsf{A}\)の固有値を\(\lambda\)、単位行列を\(\mathsf{I}\)とすると、特性方程式より
\begin{gather}
\text{det}[\mathsf{A}-\lambda\mathsf{I}]=0 \\
\text{det}\left[\begin{pmatrix}2-\lambda & -1 \\ -1 &2-\lambda\end{pmatrix}\right]=0 \\
(2-\lambda)^{2}-1=0 \\
\lambda^{2}-4\lambda+3=0 \\
(\lambda-1)(\lambda-3)=0 & \therefore \lambda_{1}=1, \lambda_{2}=3 \tag{2-2}\label{lambda}
\end{gather}
となる。
さらに\(\mathsf{A}\)の固有ベクトルを\(\vec{q}_{1}=(a,b)^{\text{T}}, \vec{q}_{2}=(c,d)^{\text{T}}\)とし、それぞれ\(\mathsf{A}\,\vec{q}_{1}=\lambda_{1}\vec{q}_{1},\,\mathsf{A}\,\vec{q}_{2}=\lambda_{2}\vec{q}_{2}\)を満たすとする。
さらに\(\mathsf{A}\)は実対称行列であるため、固有ベクトルは正規直交基底をなすようにることができ、
\begin{align*}
&\begin{pmatrix}2 & -1 \\ -1 &2\end{pmatrix}\begin{pmatrix}a \\ b\end{pmatrix}=\begin{pmatrix}a \\ b\end{pmatrix} \quad\Longrightarrow\quad\begin{cases}2a-b=a \\ -a+2b=b\end{cases} &&\therefore \vec{q}_{1}=\frac{1}{\sqrt{2}}\begin{pmatrix}1 \\1\end{pmatrix} \tag{2-3}\label{q1}\\
&\begin{pmatrix}2 & -1 \\ -1 &2\end{pmatrix}\begin{pmatrix}c \\ d\end{pmatrix}=3\begin{pmatrix}c \\ d\end{pmatrix} \quad\Longrightarrow\quad\begin{cases}2c-d=3c \\ -c+2d=3d\end{cases} &&\therefore \vec{q}_{2}=\frac{1}{\sqrt{2}}\begin{pmatrix}-1 \\1\end{pmatrix} \tag{2-4}\label{q2}
\end{align*}
と求められる。
ここで行列\(\mathsf{O}\)を次式で定義する。
\begin{align}
\mathsf{O}=(\vec{q}_{1}\quad\vec{q}_{2})=\frac{1}{\sqrt{2}}\begin{pmatrix}1 & -1\\1 &1\end{pmatrix} \tag{2-5}\label{gyouretuo}
\end{align}
\(\mathsf{O}\)は直交行列であるため、その逆行列\(\mathsf{O}^{-1}\)は転置行列\(\mathsf{O}^{\text{T}}\)に等しい。
\begin{align}
\mathsf{O}^{-1}=\mathsf{O}^{\text{T}}=\frac{1}{\sqrt{2}}\begin{pmatrix}1&1\\-1&1\end{pmatrix} \tag{2-6}\label{ogyaku}
\end{align}
このとき、
\begin{align}
\mathsf{O}^{\text{T}}\mathsf{AO}=\begin{pmatrix}1&0\\0&3\end{pmatrix}=\begin{pmatrix}\lambda_{1}&0\\0&\lambda_{2}\end{pmatrix}=\Lambda \tag{2-7}\label{lambdagyo}
\end{align}
が成り立ち、
\begin{align}
\mathsf{A}=\mathsf{O}\Lambda\mathsf{O}^{\text{T}} \tag{2-8}\label{ataikaku}
\end{align}
となる。
これで\(\mathsf{A}\)を対角化することができた。
②に続く。





コメント