前回
にて偏光と偏光パラメータについて解説した。
偏光パラメータは偏光状態を特徴づけるパラメータだが、直接測定は難しい。
そこで登場するのがストークスパラメータである。
本記事ではストークスパラメータと、偏光の変化を記述するミューラー行列を導入し、偏光の偏光状態をストークスパラメータを利用して特定する手法を解説していく。
ストークスパラメータとストークスベクトル
ある偏光の光強度を\(I\)、振幅比角を\(\psi\)、位相差を\(\delta\)を用いて、次の4つのパラメータを定義する。
\begin{align}
&S_{0}=I \label{s0}\\
&S_{1}=I\cos2\psi \label{s1}\\
&S_{2}=I\sin2\psi\cos\delta \label{s2}\\
&S_{3}=I\sin2\psi\sin\delta \label{s3}
\end{align}
上記4つのパラメータをストークスパラメータと呼び、これらを並べたベクトル
\begin{align}
\vec{S}=\begin{pmatrix}S_{0}\\S_{1}\\S_{2}\\S_{3}\end{pmatrix}=\begin{pmatrix}I\\I\cos2\psi\\I\sin2\psi\cos\delta\\I\sin2\psi\sin\delta\end{pmatrix}\label{svec}
\end{align}
をストークスベクトルと呼ぶ。
ストークスパラメータを見て、三次元極座標表示を連想した人もいると思う。
実際に\(S_{1},S_{2},S_{3}\)が直交する三次元座標系を考えると、\(I,\psi,\delta\)はこの三次元直交座標系を極座標変換した際のパラメータになっている。
\((x,y,z)\to(r,\theta,\phi)\)
\begin{align}
\begin{cases}
x=r\sin\theta\cos\phi \\
y=r\sin\theta\sin\phi \\
z=r\cos\theta
\end{cases}\begin{pmatrix}
0\leq r \leq \infty\\ 0\leq \theta \leq \pi\\ 0\leq \phi <2\pi
\end{pmatrix}
\end{align}
\((S_{1},S_{2},S_{3})\to(I,\psi,\delta)\)
\begin{align}
\begin{cases}
S_{2}=I\sin2\psi\cos\delta \\
S_{3}=I\sin2\psi\sin\delta \\
S_{1}=I\cos2\psi
\end{cases}\begin{pmatrix}
0\leq I \leq \infty\\ 0\leq 2\psi \leq \pi \\0\leq \delta <2\pi
\end{pmatrix}
\end{align}
具体的に\((x,y,z)\)が決まれば\((r,\theta,\phi)\)が決まるように、\((S_{1},S_{2},S_{3})\)が決まれば\((I,\psi,\delta)\)が決まる。
すなわちこのとから、ストークスパラメータが決まれば強度と偏光パラメータが決まり、偏光の偏光状態を特定することができる。
特に強度\(I\)が同じ偏光状態はすべて、\(S_{1},S_{2},S_{3}\)の座標系において半径\(I\)の球面上に存在し、この球をポアンカレ球と呼ぶ。
ミューラー行列
概要
ある偏光の偏光状態が物質との相互作用によって変化した場合を考える。
変化前の偏光状態がストークスベクトル\(\vec{S}\)で、変化後の偏光状態がストークスベクトル\(\vec{S}’\)で記述できるとき、その変化の過程は4次の正方行列\(\mathsf{M}\)を用いて
\begin{align}
\vec{S}’=\mathsf{M}\vec{S}
\end{align}
と書き表すのが自然である。
\(\mathsf{M}\)をミューラー行列と呼び、偏光に変化をもたらす光学素子はこのミューラー行列によって記述される。
代表的な光学素子のミューラー行列を下に挙げておこう。
| 光学素子 | ミューラー行列 |
| 偏光子 (透過軸回転角\(0\)(水平)) \(\mathsf{P}(0)\) | \(\displaystyle{\frac{1}{2}\begin{pmatrix}1&1&0&0\\1&1&0&0\\0&0&0&0\\0&0&0&0\end{pmatrix}}\) |
| 偏光子 (透過軸回転角\(\pi/2\)(垂直)) \(\mathsf{P}(\pi/2)\) | \(\displaystyle{\frac{1}{2}\begin{pmatrix}1&-1&0&0\\-1&1&0&0\\0&0&0&0\\0&0&0&0\end{pmatrix}}\) |
| 偏光子 (透過軸回転角\(\pi/4\)) \(\mathsf{P}(\pi/4)\) | \(\displaystyle{\frac{1}{2}\begin{pmatrix}1&0&1&0\\0&0&0&0\\1&0&1&0\\0&0&0&0\end{pmatrix}}\) |
| 偏光子 (透過軸回転角\(-\pi/4\)) \(\mathsf{P}(-\pi/4)\) | \(\displaystyle{\frac{1}{2}\begin{pmatrix}1&0&-1&0\\0&0&0&0\\-1&0&1&0\\0&0&0&0\end{pmatrix}}\) |
| 偏光子 (透過軸回転角\(\theta\)) \(\mathsf{P}(\theta)\) | \(\displaystyle{\frac{1}{2}\begin{pmatrix}1&\cos2\theta&\sin2\theta&0\\ \cos2\theta&\cos^{2}2\theta&\sin2\theta\cos2\theta&0\\ \sin2\theta&\sin2\theta\cos2\theta&\sin^{2}2\theta&0\\0&0&0&0\end{pmatrix}}\) |
| \(\lambda/4\)板 (位相差\(\pi/2\),fast軸回転角\(0\)(水平)) \(\mathsf{C}(\pi/2,0)\) | \(\displaystyle{\begin{pmatrix}1&0&0&0\\ 0&1&0&0\\ 0&0&0&1\\0&0&-1&0\end{pmatrix}}\) |
| \(\lambda/4\)板 (位相差\(\pi/2\),fast軸回転角\(\pi/2\)(垂直)) \(\mathsf{C}(\pi/2,\pi/2)\) | \(\displaystyle{\begin{pmatrix}1&0&0&0\\ 0&1&0&0\\ 0&0&0&-1\\0&0&1&0\end{pmatrix}}\) |
| 位相子 (位相差\(\varphi\),fast軸回転角\(0\)(水平)) \(\mathsf{C}(\varphi,0)\) | \(\displaystyle{\begin{pmatrix}1&0&0&0\\ 0&1&0&0\\ 0&0&\cos\varphi&\sin\varphi\\0&0&-\sin\varphi&\cos\varphi\end{pmatrix}}\) |
| 位相子 (位相差\(\varphi\),fast軸回転角\(\pi/2\)(垂直)) \(\mathsf{C}(\varphi,\pi/2)\) | \(\displaystyle{\begin{pmatrix}1&0&0&0\\ 0&1&0&0\\ 0&0&\cos\varphi&-\sin\varphi\\0&0&\sin\varphi&\cos\varphi\end{pmatrix}}\) |
| 位相子 (位相差\(\varphi\),fast軸回転角\(\theta\)) \(\mathsf{C}(\varphi,\theta)\) | \(\displaystyle{\begin{pmatrix}1&0&0&0\\ 0&\cos^{2}2\theta+\cos\varphi\sin^{2}2\theta&(1-\cos\varphi)\sin2\theta\cos2\theta&-\sin\varphi\sin2\theta\\ 0&(1-\cos\varphi)\sin2\theta\cos2\theta&\sin^{2}2\theta+\cos\varphi\cos^{2}2\theta&\sin\varphi\cos2\theta\\0&\sin\varphi\sin2\theta&-\sin\varphi\cos2\theta&\cos\varphi\end{pmatrix}}\) |
また一般的に、光学素子\(\mathsf{M}\)を角度\(\theta\)回転させたときのミューラー行列は回転行列
\begin{align}
\mathsf{R}(\theta)=\begin{pmatrix}
1&0&0&0\\0&\cos2\theta&-\sin2\theta&0 \\ 0&\sin2\theta&\cos2\theta&0 \\0&0&0&1
\end{pmatrix}
\end{align}
を用いて
\begin{align}
\mathsf{R}(\theta)\mathsf{M}\mathsf{R}(-\theta)
\end{align}
と書ける。
例1
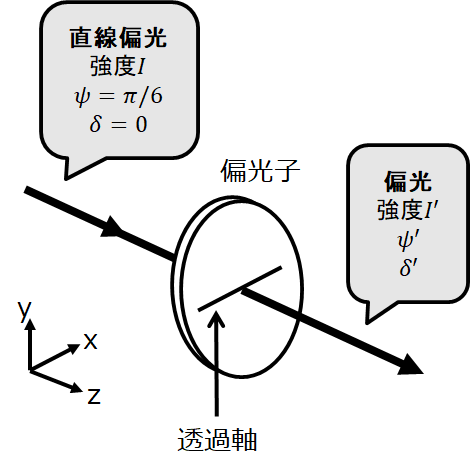
強度\(I\)、振幅比角\(\psi=\pi/6\)、位相差\(\delta=0\)の偏光を考える。
これは振幅比(傾き)\(E_{0y}/E_{0x}=1/2\)の直線偏光である。
この直線偏光を偏光子に入射させる。
ただし、偏光子の透過軸は水平(x軸に平行)とする。
このとき、直線偏光のストークスベクトルを\(\vec{S}\)、偏光子のミューラー行列を\(\mathsf{P}(0)\)、偏光子透過後の偏光のストークスベクトルを\(\vec{S}’\)とすると
\begin{align}
\vec{S}’&=\mathsf{P}(0)\vec{S} \notag \\
&=\frac{1}{2}\begin{pmatrix}
1&1&0&0 \\ 1&1&0&0 \\ 0&0&0&0 \\ 0&0&0&0
\end{pmatrix}\begin{pmatrix}
I\\I\cos(\pi/3)\\I\sin(\pi/3)\cos 0\\I\sin(\pi/3)\sin 0
\end{pmatrix} \notag \\
&=\frac{1}{2}\begin{pmatrix}
1&1&0&0 \\ 1&1&0&0 \\ 0&0&0&0 \\ 0&0&0&0
\end{pmatrix}\begin{pmatrix}
I\\I/2\\ \sqrt{3}I/2\\0
\end{pmatrix}=\frac{1}{2}\begin{pmatrix}
3I/2\\3I/2\\0\\0
\end{pmatrix}=\frac{3I}{4}\begin{pmatrix}
1\\1\\0\\0
\end{pmatrix}\label{rei1-1}\tag{1}
\end{align}
となる。
透過軸が水平な偏光子に偏光が入射すると、x軸に平行な成分(水平偏光)のみが出射する。
水平偏光では振幅比角が0となるため、ストークスベクトルは
\begin{align}
\vec{S}’=\begin{pmatrix}
I’\\I’\\0\\0
\end{pmatrix}=I’\begin{pmatrix}
1\\1\\0\\0
\end{pmatrix}
\end{align}
となり、ベクトルの成分は(\ref{rei1-1})と合致し、強度は元の偏光の3/4倍になることがわかる。
例2
強度\(I\)、振幅比角\(\psi=\pi/4\)、位相差\(\delta=0\)の偏光を考える。
これは振幅比(傾き)\(E_{0y}/E_{0x}=1\)の直線偏光である。
この直線偏光を\(\lambda/4\)板(1/4波長板)に入射させる。
ただし、\(\lambda/4\)板のfast軸が垂直(y軸に平行)であるとする。
このとき、直線偏光のストークスベクトルを\(\vec{S}\)、\(\lambda/4\)板のミューラー行列を\(\mathsf{C}(\pi/2,\pi/2)\)、偏光子透過後の偏光のストークスベクトルを\(\vec{S}’\)とすると

\begin{align}
\vec{S}’&=\mathsf{C}(\pi/2,\pi/2)\vec{S} \notag \\
&=\begin{pmatrix}
1&0&0&0 \\ 0&1&0&0 \\ 0&0&0&-1 \\ 0&0&1&0
\end{pmatrix}\begin{pmatrix}
I\\I\cos(\pi/2)\\I\sin(\pi/2)\cos 0\\I\sin(\pi/2)\sin 0
\end{pmatrix} \notag \\
&=\begin{pmatrix}
1&0&0&0 \\ 0&1&0&0 \\ 0&0&0&-1 \\ 0&0&1&0
\end{pmatrix}\begin{pmatrix}
I\\0\\I\\0
\end{pmatrix}=\begin{pmatrix}
I\\0\\0\\I
\end{pmatrix}=I\begin{pmatrix}
1\\0\\0\\1
\end{pmatrix}\label{rei1-2}\tag{2}
\end{align}
となる。
\(\lambda/4\)板は名前の通り、fast軸とslow軸を通る2つの電場の位相差を1/4波長分、すなわち\(\pi/2\)ずらす。
今回の場合、fast軸がy軸に平行であるため、y方向の電場がx方向の電場に対して1/4波長分進んで出射される。
振幅比1の直線偏光がこの\(\lambda/4\)板を透過すると、出射後は時計回り円偏光になる。
時計回り円偏光は\(\psi=\pi/4\)、位相差\(\delta=\pi/2\)となるため、ストークスベクトルは
\begin{align}
\vec{S}’=\begin{pmatrix}I’\\I’\cos(\pi/2)\\I’\sin(\pi/2)\cos(\pi/2)\\I’\sin(\pi/2)\sin(\pi/2)\end{pmatrix}=\begin{pmatrix}I’\\0\\0\\I’\end{pmatrix}=I’\begin{pmatrix}1\\0\\0\\1\end{pmatrix}
\end{align}
となり、ベクトルの成分は(\ref{rei1-2})と合致し、強度は元の偏光と同じになることがわかる。
ストークスパラメータを用いた偏光状態特定
ある偏光の偏光状態(x-y平面上で電場が描く軌跡の種類と電場が動く方向)を特定したい状況を考える。
このとき偏光の振幅比角\(\psi\)と位相差\(\delta\)の両方を調べる必要があるが、これらを直接測定するのは難しい。
しかしストークスパラメータを使うと、直接測定が困難なこの\(\psi\)と\(\delta\)を光強度の測定のみで求めることができる。
以下、\(\psi\)と\(\delta\)を求めたい偏光のストークスベクトルを\(\vec{S}=(S_{0},S_{1},S_{2},S_{3})^{\text{T}}\)として具体的な方法を示す。
ただし、\(I\)は求めたい偏光の全強度である。
測定1
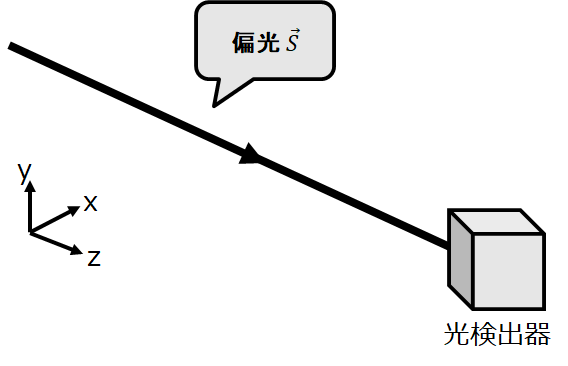
まず偏光の全強度を測定する。
これはストークスパラメータの第1成分\(S_{0}\)に相当する。
測定2
次に、偏光を回転角0(透過軸が水平)の偏光子に入射し、出射後の偏光の強度を測定する。
このとき、出射後の偏光のストークスベクトルを\(\vec{S}^{(1)}=(S_{0}^{(1)},S_{1}^{(1)},S_{2}^{(1)},S_{3}^{(1)})^{\text{T}}\)とすると、
\begin{align}
&&\vec{S}^{(1)}&=\mathsf{P}(0)\vec{S} \notag \\
&&\begin{pmatrix}
S_{0}^{(1)}\\ S_{1}^{(1)}\\ S_{2}^{(1)}\\ S_{3}^{(1)}
\end{pmatrix}
&=\frac{1}{2}\begin{pmatrix}1&1&0&0\\1&1&0&0\\0&0&0&0\\0&0&0&0\end{pmatrix}\begin{pmatrix}
S_{0}\\ S_{1}\\ S_{2}\\ S_{3}
\end{pmatrix}=\frac{1}{2}\begin{pmatrix}
S_{0}+S_{1}\\ S_{0}+S_{1}\\ 0\\ 0
\end{pmatrix}
\end{align}
が成立する。
出射後の偏光の強度はストークスベクトルの第1成分\(S_{0}^{(1)}=(S_{0}+S_{1})/2\)に相当する。

測定3
続いて、偏光を回転角\(\pi/4\)の偏光子に入射し、出射後の偏光の強度を測定する。
このとき、出射後の偏光のストークスベクトルを\(\vec{S}^{(2)}=(S_{0}^{(2)},S_{1}^{(2)},S_{2}^{(2)},S_{3}^{(2)})^{\text{T}}\)とすると、
\begin{align}
&&\vec{S}^{(2)}&=\mathsf{P}(\pi/4)\vec{S} \notag \\
&&\begin{pmatrix}
S_{0}^{(2)}\\ S_{1}^{(2)}\\ S_{2}^{(2)}\\ S_{3}^{(2)}
\end{pmatrix}
&=\frac{1}{2}\begin{pmatrix}1&0&1&0\\0&0&0&0\\1&0&1&0\\0&0&0&0\end{pmatrix}\begin{pmatrix}
S_{0}\\ S_{1}\\ S_{2}\\ S_{3}
\end{pmatrix}=\frac{1}{2}\begin{pmatrix}
S_{0}+S_{2}\\ 0\\ S_{0}+S_{2}\\ 0
\end{pmatrix}
\end{align}
が成立する。
出射後の偏光の強度はストークスベクトルの第1成分\(S_{0}^{(2)}=(S_{0}+S_{2})/2\)に相当する。

測定4
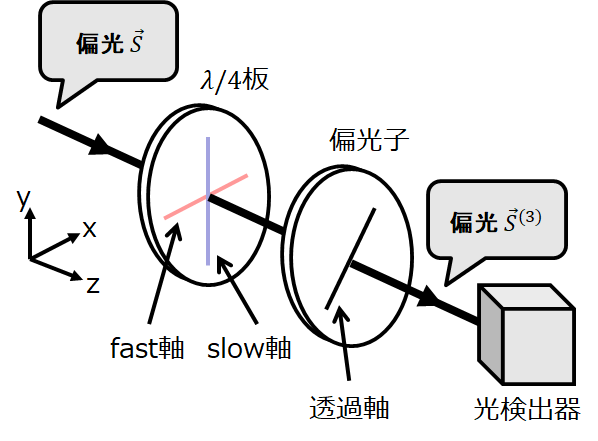
最後に、偏光を回転角0(fast軸が水平)の\(\lambda/4\)板に入射し、出射後の偏光をさらに回転角\(\pi/4\)の偏光子に入射し、出射後の強度を測定する。
このとき、出射後の偏光のストークスベクトルを\(\vec{S}^{(3)}=(S_{0}^{(3)},S_{1}^{(3)},S_{2}^{(3)},S_{3}^{(3)})^{\text{T}}\)とすると、
\begin{align}
&&\vec{S}^{(3)}&=\mathsf{P}(\pi/4)\mathsf{C}(\pi/2,0)\vec{S} \notag \\
&&\begin{pmatrix}
S_{0}^{(3)}\\ S_{1}^{(3)}\\ S_{2}^{(3)}\\ S_{3}^{(3)}
\end{pmatrix}
&=\frac{1}{2}\begin{pmatrix}1&0&1&0\\0&0&0&0\\1&0&1&0\\0&0&0&0\end{pmatrix}\begin{pmatrix}1&0&0&0\\ 0&1&0&0\\ 0&0&0&1\\0&0&-1&0\end{pmatrix}\begin{pmatrix}
S_{0}\\ S_{1}\\ S_{2}\\ S_{3}
\end{pmatrix} \notag \\
&& &=\frac{1}{2}\begin{pmatrix}1&0&0&1\\ 0&0&0&0\\ 1&0&0&1\\0&0&0&0\end{pmatrix}\begin{pmatrix}
S_{0}\\ S_{1}\\ S_{2}\\ S_{3}
\end{pmatrix}=\frac{1}{2}\begin{pmatrix}
S_{0}+S_{3} \\ 0 \\ S_{0}+S_{3}\\ 0
\end{pmatrix}
\end{align}
が成立する。
出射後の偏光の強度はストークスベクトルの第1成分\(S_{0}^{(3)}=(S_{0}+S_{3})/2\)に相当する。
以上の結果をまとめると
\begin{align}
\begin{cases}
\displaystyle{S_{0}^{(1)}=\frac{S_{0}+S_{1}}{2}}\\ \\
\displaystyle{S_{0}^{(2)}=\frac{S_{0}+S_{2}}{2}}\\ \\
\displaystyle{S_{0}^{(3)}=\frac{S_{0}+S_{3}}{2}}
\end{cases}
\end{align}
となるため、これを式変形すると
\begin{align}
\begin{cases}
S_{1}=2S_{0}^{(1)}-S_{0}\\
S_{2}=2S_{0}^{(2)}-S_{0}\\
S_{3}=2S_{0}^{(3)}-S_{0}
\end{cases}
\end{align}
となる。
\(S_{0},S_{0}^{(1)},S_{0}^{(2)},S_{0}^{(3)}\)は全て測定によって得られた光強度である。
以上で光強度測定のみで偏光のストークスパラメータを決定できたので、偏光の偏光状態も決定できる。
終わりに
偏光を勉強していて、自分はつくづくこの手のイメージ力が無いんだなと思い知らされる。
大学で勉強して、会社でも使うことが出てきて、断続的にではあるが10年偏光と向き合っているのに未だに明快な説明をするのが難しい。
それでもここまで記事にできらことは一つの成長とポジティブに捉えることにしたい。
会社で結構ガチな物理を扱う場面が増えてきたから、その辺りに絡めた記事も書きたい。
END




コメント