高校物理の力学で扱う物体はほぼ質点であり、物体の大きさを無視して考える。
だが剛体のつりあいは例外であり、物体に大きさが存在し、力のかかり方に大きく影響してくる。
しかし物体が大きさを持っても、つりあっている条件下ならやることはほぼ決まっている。
本記事では、剛体のつりあいの問題を解く定石の手法を解説し、例題を交えてその手法の適用方法を示す。
問題の解法
剛体のつりあいの問題の解法は下記の通りである。
① 剛体にはたらいている力を全て探す。
② 力のつりあいの式を立てる。
③ 任意の点(指定があればその点)のまわりの力のモーメントのつりあいの式を立てる。
④ ②、③で立てた式を連立方程式として解く。
①、②までは質点のつりあいの問題と同じである。
③が剛体特有のステップであり、これさえ通過すれば後は②で立てた式とで連立させるだけである。
簡単に復習しておくと、力のモーメント\(M\)は、剛体にかかる力\(F\)と、\(F\)の作用線(延長線)と回転軸までの距離\(\ell\)の積で表される(図1参照)。
\begin{align}
M=F\ell
\end{align}
力の作用線上に回転軸がある場合、\(\ell=0\)となるため力のモーメントも0になることに注意。
力のモーメントの正負は剛体の回転方向で決まり、一般的には反時計回りに回す場合に正、時計回りに回す場合に負となる。
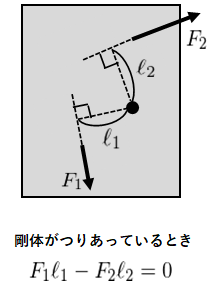
そして剛体がつりあっている(静止、または等速運動している)とき、力のモーメントの総和は0になる。
では上記を念頭に入れた上で、実際に例題を解いてみる。
例題1
例題1
右図のように、長さ\(1.0\,\text{m}\)の軽い棒の両端A、Bに、それぞれ重さが\(30\,\text{N},20\,\text{N}\)のおもりをつるし、点Oにばね定数\(2.5\times10^{2}\,\text{N/m}\)の軽いばねをつけてつるしたところ、棒は水平になって静止した。
(1) ばねの伸びを\(x\text{[m]}\)とし、鉛直方向の力のつりあいの式を立てよ。
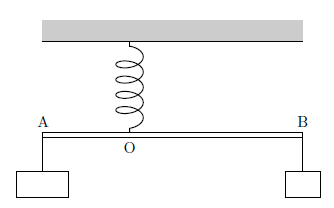
(2) AOの長さを\(y\text{[m]}\)とし、ばねと棒の接点Oを回転軸にとって、力のモーメントのつりあいの式を立てよ。
(3) ばねの伸び\(x\text{[m]}\)および、AOの長さ\(y\text{[m]}\)を求めよ。
ただし、おもりは質点とみなせるとする。
解説
上述の解法のステップを踏んで解いてみる。
① まず棒にかかる力をすべて書き出すと図3のようになる。
② 今回は棒に水平方向の力がはたらいていないため、鉛直方向の力のみを考えれば十分である。
鉛直上向きを正とすると、図3より鉛直方向の力のつりあいの式は次のようになる。
\begin{gather}
(+2.5\times10^{2}x)+(-30)+(-20)=0\\ \therefore 2.5\times10^{2}x-30-20=0 \label{for.1.1}\tag{1}
\end{gather}
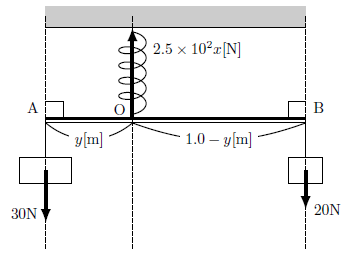
③ 今回は「ばねと棒の接点Oを回転軸にとって」という指定があるため、点Oまわりの力のモーメントのつりあいの式を立てる。
図2から力のモーメントのつりあいの式は次のようになる。
(ばねからの張力は作用線上に回転軸Oがあるので省略。)
\begin{align}
(+30\times{y})+\{-20\times{(1.0-y)}\}=0 \qquad \therefore 30y-20(1.0-y)=0 \label{for.1.2}\tag{2}
\end{align}
④ ②と③で立てた式(\ref{for.1.1})、(\ref{for.1.2})を連立方程式とみなして解くと、次のような結果となる(連立方程式とはいっても、それぞれが\(x,y\)の1次方程式なのだが)。
\begin{align}
x=0.20\,\text{m} \qquad y=0.40\,\text{m}
\end{align}
これで①~④までの手順を全て踏んだわけだが、実はこれでもう問題はすべて解けてしまっている。
(1) (\ref{for.1.1})より、\(\boxed{2.5\times10^{2}x-30-20=0}\)
(2) (\ref{for.1.2})より、\(\boxed{30y-20(1.0-y)=0}\)
(3) ④の結果より、\(\boxed{x=0.20\,\text{m},y=0.40\,\text{m}}\)
例題2
例題2
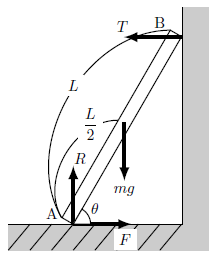
右図のように、なめらかな壁と摩擦のある床に、一様な太さの棒を立てかける。
ただし、棒と床がなす角を\(\theta\)、棒の質量を\(m\)、棒の長さを\(L\)、重力加速度の大きさを\(g\)とする。
また、棒が受ける壁からの垂直抗力の大きさを\(T\)、水平面からの垂直抗力の大きさを\(R\)、水平面からの摩擦力の大きさを\(F\)とする。
(1) 水平方向と鉛直方向の力のつりあいの式をそれぞれ立てよ。
(2) 水平面と棒の接点Aを回転軸にとって、力のモーメントのつりあいの式を立てよ。
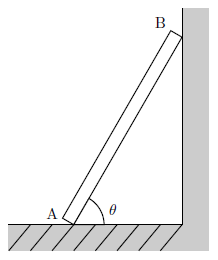
(3) (1)、(2)で立てた3つの式を連立方程式と見なし、\(R, T, F\)をそれぞれ\(m, g, \theta\)を用いて表わせ。
解説
壁に立てかけた棒のつりあいに関する問題。
剛体のつりあいでは頻出のパターンである。
先ほどと同様に、先述した解法のステップを踏んで解いてみる。
① まず棒にかかる力をすべて書き出すと図5のようになる。
問題文中に「一様な太さの棒」とあるが、これは「棒にはたらく重力は、すべて棒の中点に加わるとしてよい」ことを示している。
② 今回は水平方向、鉛直方向の両方の力を考える必要がある。
右向き、鉛直上向きを正とすると、図5より水平方向の力のつりあいの式は次のようになる。
\begin{align}
(+F)+(-T)=0 \qquad \therefore F-T=0 \label{for.2.1}\tag{3}
\end{align}
さらに図5より鉛直方向の力のつりあいの式は次のようになる。
\begin{align}
(+R)+(-mg)=0 \qquad \therefore R-mg=0 \label{for.2.2}\tag{4}
\end{align}
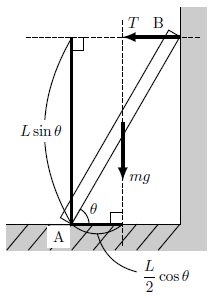
③ 今回は「水平面と棒の接点Aを回転軸にとって」という指定があるため、点Aまわりの力のモーメントのつりあいの式を立てる。
図6より力のモーメントのつりあいの式は次のようになる。
(\(R,\,F\)は作用線上に回転軸Aがあるので省略。)
\begin{gather}
\left(-mg\times{\frac{L}{2}\cos{\theta}}\right)+(T\times L\sin{\theta})=0 \\
\therefore TL\sin\theta-\frac{mgL\cos\theta}{2}=0 \label{for.2.3}\tag{5}
\end{gather}
④ ②と③で立てた式(\ref{for.2.1})~(\ref{for.2.3})を連立方程式とみなして解く。
まず式(\ref{for.2.2})より、
\begin{align}
R=mg \label{for.2.4}\tag{6}
\end{align}
となる。続いて式(\ref{for.2.3})より、
\begin{align}
TL\sin\theta=\frac{mgL\cos\theta}{2} \qquad \therefore T=\frac{mg}{2\tan\theta} \qquad \left(\displaystyle{\tan\theta=\frac{\sin\theta}{\cos\theta}}\text{より}\right) \label{for.2.5}\tag{7}
\end{align}
となる。そして式(\ref{for.2.5})を式(\ref{for.2.1})に代入すると、次のようになる。
\begin{align}
F-\frac{mg}{2\tan\theta}=0 \qquad \therefore F=\frac{mg}{2\tan\theta} \label{for.2.6}\tag{8}
\end{align}
この問題も、この時点で既に全問解答できている。
(1) (\ref{for.2.1})、(\ref{for.2.2})より、\(\boxed{水平方向:F-T=0、鉛直方向:R-mg=0}\)
(2) (\ref{for.2.3})より、\(\boxed{\displaystyle{TL\sin\theta-\frac{mgL\cos\theta}{2}=0}}\)
(3) (\ref{for.2.4})~(\ref{for.2.6})より、\(\boxed{\displaystyle{R=mg,\, T=F=\frac{mg}{2\tan\theta}}}\)
例題3
例題3
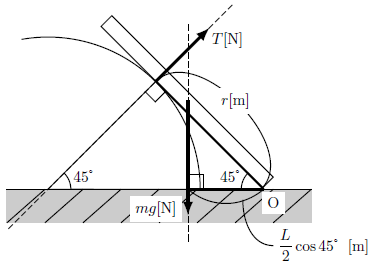
右図のように、水平面上に固定された半径\(r[\text{m}]\)のなめらかな半円柱に、長さ\(L[\text{m}]\)、質量\(m[\text{kg}]\)の太さと密度の一様な棒が、水平面と\(45\text{°}\)の角度で立てかけてある。
このとき、棒が受ける半円柱からの垂直抗力の大きさを\(T[\text{N}]\)、水平面からの垂直抗力の大きさを\(R[\text{N}]\)、水平面からの摩擦力の大きさを\(F[\text{N}]\)とする。また、重力加速度の大きさを\(g[\text{m/s}^{2}]\)とする。
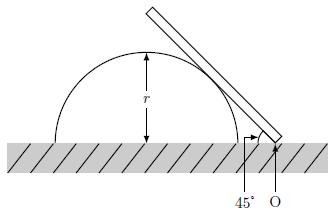
(1) 水平方向と鉛直方向の力のつりあいの式をそれぞれ立てよ。
(2) 水平面と棒の接点Oを回転軸にとって、力のモーメントのつりあいの式を立てよ。
(3) (1)、(2)で立てた3つの式を連立方程式と見なし、\(T, F, R\)をそれぞれ\(L, r, m, g\)を用いて表わせ。
解説
円柱に立てかけた棒のつりあいに関する問題。
どの位置で棒と円柱が接するのか一瞬迷うかもしれないが、実は円の性質を使えば接する位置がごく自然に決まる。
物理の問題としてだけでなく、数学の図形の問題として視点を切り替えて見ることができるかがカギになる問題だ。
ここでも早速、上述の解法を適用してみる。
① まず棒にかかる力をすべて書き出すと図8のようになる。
「太さと密度の一様な太さの棒」を扱うため、棒にはたらく重力は、すべて棒の中点に加わるとしてよい。
迷うとすれば半円柱から受ける垂直抗力\(T\)が加わる位置だが、これは円と接線の関係を考えればよい。
円の接線は、接点を通る半径と直交する。
この事実を利用すれば、点O、円柱と棒の接点、円柱の中心の3点を各頂点とした直角二等辺三角形が出現することがわかる。
よって、垂直抗力\(T\)は棒の下端Oから\(r[\text{m}]\)の位置に加わることがわかる。
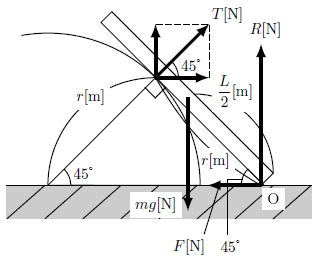
② 今回は水平方向、鉛直方向の両方の力を考える必要がある。
垂直抗力\(T\)は水平成分と鉛直成分に分解して、各分力を各成分のつりあいの式に組み入れればよい。
右向き、鉛直上向きを正とすると、図8より水平方向の力のつりあいの式は次のようになる。
\begin{align}
(+T\cos{45°})+(-F)=0 \qquad \therefore \frac{T}{\sqrt{2}}-F=0 \label{for.3.1}\tag{9}
\end{align}
さらに図8より鉛直方向の力のつりあいの式は次のようになる。
\begin{align}
(+R)+(+T\sin{45°})+(-mg)=0 \qquad \therefore R+\frac{T}{\sqrt{2}}-mg=0 \label{for.3.2}\tag{10}
\end{align}
③ 今回は「水平面と棒の接点Oを回転軸にとって」という指定があるため、点Oまわりの力のモーメントのつりあいの式を立てる。
図9より力のモーメントのつりあいの式は次のようになる。
(\(R,\,F\)は作用線上に回転軸があるので省略。)
\begin{align}
&\left(+mg\times{\frac{L}{2}\cos{45°}}\right)+(-T\times r)=0\\ &\therefore \frac{\sqrt{2}mgL}{4}-Tr=0 \label{for.3.3}\tag{11}
\end{align}
④ ②と③で立てた(\ref{for.3.1})~(\ref{for.3.3})を連立方程式とみなして解く。
まず(\ref{for.3.3})より、
\begin{align}
Tr=\frac{\sqrt{2}mgL}{4} \qquad \therefore T=\frac{\sqrt{2}mgL}{4r}\,[\mathrm{N}] \label{for.3.4}\tag{12}
\end{align}
となる。
よって(\ref{for.3.4})を(\ref{for.3.1})に代入して、
\begin{align}
\frac{1}{\sqrt{2}}\cdot\frac{\sqrt{2}mgL}{4r}-F=0 \qquad \therefore F=\frac{mgL}{4r}\,[\mathrm{N}] \label{for.3.5}\tag{13}
\end{align}
となる。
そして(\ref{for.3.4})を(\ref{for.3.2})に代入すると、次のようになる。
\begin{align}
R+\frac{1}{\sqrt{2}}\cdot\frac{\sqrt{2}mgL}{4r}-mg=0 \qquad \therefore R=mg\left(1-\frac{L}{4r}\right)[\mathrm{N}] \label{for.3.6}\tag{14}
\end{align}
こちらもこの時点で全問解答している。
(1) (\ref{for.3.1})、(\ref{for.3.2})より、\(\boxed{水平方向:\displaystyle{\frac{T}{\sqrt{2}}-F=0}、鉛直方向:\displaystyle{R+\frac{T}{\sqrt{2}}-mg=0}}\)
(2) (\ref{for.3.3})より、\(\boxed{\displaystyle{\frac{\sqrt{2}mgL}{4}-Tr=0}}\)
(3) (\ref{for.3.4})~(\ref{for.3.6})の結果より、\(\boxed{\displaystyle{T=\frac{\sqrt{2}mgL}{4r}\,[\text{N}],\,F=\frac{mgL}{4r}\,[\text{N}],\,R=mg\left(1-\frac{L}{4r}\right)[\text{N}]}}\)
終わりに
剛体がつりあっている状況であれば、決まった解法で力を求められることを見てきた。
次は応用になるわけだが、剛体のつりあいの応用問題はほぼ「つりあいが崩れない条件を調べる」問題である。
次の記事では今回用いた例題を再利用し、つりあいが崩れない条件を調べる問題を扱うことにする。
次回はこちら。





コメント