【解析力学】3質点の連成振動～オイラー・ラグランジュ方程式の利用例～③

　下記の続き。

　ここでは、3質点の連成振動の具体的な運動を見ていく。

解答(4)

　(3)より、\(x_{\text{a}}(t), x_{\text{b}}(t) , x_{\text{c}}(t)\)の一般解は

\begin{align}
\begin{cases}
\displaystyle{x_{\text{a}}(t)=\frac{1}{2}\left\{\sqrt{2}\,C_{\text{a}}\cos(\omega_{\text{a} }t+\phi_{\text{a}})+C_{\text{b}}\cos( \omega_{\text{b}}t+\phi_{\text{b}})+ C_{\text{c}}\cos(\omega_{\text{c}} t+\phi_{\text{c}})\right\}}\\
\displaystyle{x_{\text{b}}(t)=\frac{1}{2}\left\{-\sqrt{2}\,C_{\text{b}}\cos( \omega_{\text{b}}t +\phi_{\text{b}})+\sqrt{2}\,C_{\text{c}}\cos(\omega_{\text{c}} t+\phi_{\text{c}})\right\} } \\
\displaystyle{x_{\text{c}}(t)=\frac{1}{2}\left\{-\sqrt{2}\,C_{\text{a}}\cos(\omega_{\text{a} }t+\phi_{\text{a}})+C_{\text{b}}\cos( \omega_{\text{b}}t+\phi_{\text{b}})+ C_{\text{c}}\cos(\omega_{\text{c}} t+\phi_{\text{c}})\right\}}
\end{cases}\tag{4-1}\label{aippan}
\end{align}

である。ただし\(\omega_{\text{a}}=\sqrt{2\,k/m},\,\omega_{\text{b}}=\sqrt{ (2+\sqrt{2}) k/m},\,\omega_{\text{c}}=\sqrt{ (2-\sqrt{2}) k/m} \)、\(C_{\text{a}}, C_{\text{b}}, C_{\text{c}},\)\(\phi_{\text{a}} , \phi_{\text{b}}, \phi_{\text{c}}\)は任意定数である。

　(\ref{aippan})に問題文の初期条件を代入し、各任意定数を決定していく。

　(i)のとき、

\begin{align}
&x_{\text{a}}(0)=\frac{1}{2}\left\{\sqrt{2}\,C_{\text{a}}\cos\phi_{\text{a}}+C_{\text{b}}\cos\phi_{\text{b}}+ C_{\text{c}}\cos\phi_{\text{c}} \right\}=-L \\
&\left.\frac{dx_{\text{a}}(t)}{dt}\right|_{t=0}=-\frac{1}{2}\left\{\sqrt{2}\,C_{\text{a}}\omega_{\text{a}}\sin\phi_{\text{a}}+C_{\text{b}}\omega_{\text{b}}\sin\phi_{\text{b}}+C_{\text{c}}\omega_{\text{c}}\sin\phi_{\text{c}} \right\} =0\\
&x_{\text{b}}(0)=\frac{1}{2}\left\{-\sqrt{2}\,C_{\text{b}}\cos \phi_{\text{b}}+\sqrt{2}\,C_{\text{c}}\cos\phi_{\text{c}}\right\} =0\\
&\left.\frac{dx_{\text{b}}(t)}{dt}\right|_{t=0}=-\frac{1}{2}\left\{-\sqrt{2}\,C_{\text{b}}\omega_{\text{b}}\sin \phi_{\text{b}}+\sqrt{2}\,C_{\text{c}} \omega_{\text{c}} \sin\phi_{\text{c}}\right\} =0\\
&x_{\text{c}}(0)=\frac{1}{2}\left\{-\sqrt{2}\,C_{\text{a}}\cos\phi_{\text{a}}+C_{\text{b}}\cos\phi_{\text{b}}+ C_{\text{c}}\cos\phi_{\text{c}} \right\}=L \\
&\left.\frac{dx_{\text{c}}(t)}{dt}\right|_{t=0}=-\frac{1}{2}\left\{-\sqrt{2}\,C_{\text{a}}\omega_{\text{a}}\sin\phi_{\text{a}}+C_{\text{b}}\omega_{\text{b}}\sin\phi_{\text{b}}+C_{\text{c}}\omega_{\text{c}}\sin\phi_{\text{c}} \right\} =0
\end{align}

すなわち

\begin{align}
& \sqrt{2}\,C_{\text{a}}\cos\phi_{\text{a}}+C_{\text{b}}\cos\phi_{\text{b}}+ C_{\text{c}}\cos\phi_{\text{c}}=-2L \tag{4-2}\label{ixa0} \\
&\sqrt{2}\,C_{\text{a}}\omega_{\text{a}}\sin\phi_{\text{a}}+C_{\text{b}}\omega_{\text{b}}\sin\phi_{\text{b}}+C_{\text{c}}\omega_{\text{c}}\sin\phi_{\text{c}} =0 \tag{4-3}\label{iva0} \\
&-\sqrt{2}\,C_{\text{b}}\cos \phi_{\text{b}}+\sqrt{2}\,C_{\text{c}}\cos\phi_{\text{c}} =0\tag{4-4}\label{ixb0} \\
& -\sqrt{2}\,C_{\text{b}}\omega_{\text{b}}\sin \phi_{\text{b}}+\sqrt{2}\,C_{\text{c}} \omega_{\text{c}} \sin\phi_{\text{c}} =0 \tag{4-5}\label{ivb0}\\
&-\sqrt{2}\,C_{\text{a}}\cos\phi_{\text{a}}+C_{\text{b}}\cos\phi_{\text{b}}+ C_{\text{c}}\cos\phi_{\text{c}}=2L \tag{4-6}\label{ixc0} \\
&-\sqrt{2}\,C_{\text{a}}\omega_{\text{a}}\sin\phi_{\text{a}}+C_{\text{b}}\omega_{\text{b}}\sin\phi_{\text{b}}+C_{\text{c}}\omega_{\text{c}}\sin\phi_{\text{c}} =0 \tag{4-7}\label{ivc0}
\end{align}

　これら(\ref{ixa0})～(\ref{ivc0})を\(C_{\text{a}}, C_{\text{b}} , C_{\text{c}} ,\phi_{\text{a}} , \phi_{\text{b}} ,\phi_{\text{c}}\)の連立方程式として解くと、\(C_{\text{a}}=-\sqrt{2}\,L,\)\(\,C_{\text{b}}= C_{\text{c}}= 0,\,\phi_{\text{a}}=0\)となる。(\(C_{\text{b}}= C_{\text{c}}= 0\)より\(\phi_{\text{b}},\, \phi_{\text{c}} \)は考えなくてよい。)

　よってこれらを代入すると、

\begin{align}
\begin{cases}
x_{\text{a}}(t)=-L\cos\left(\omega_{\text{a}} t\right) \\
x_{\text{b}}(t)=0 \\
x_{\text{c}}(t)=L\cos(\omega_{\text{a}} t)
\end{cases}\tag{4-8}\label{ikai}
\end{align}

となる。

　続いて(ii)のとき、

\begin{align}
&x_{\text{a}}(0)=\frac{1}{2}\left\{\sqrt{2}\,C_{\text{a}}\cos\phi_{\text{a}}+C_{\text{b}}\cos\phi_{\text{b}}+ C_{\text{c}}\cos\phi_{\text{c}} \right\}=0 \\
&\left.\frac{dx_{\text{a}}(t)}{dt}\right|_{t=0}=-\frac{1}{2}\left\{\sqrt{2}\,C_{\text{a}}\omega_{\text{a}}\sin\phi_{\text{a}}+C_{\text{b}}\omega_{\text{b}}\sin\phi_{\text{b}}+C_{\text{c}}\omega_{\text{c}}\sin\phi_{\text{c}} \right\} =V\\
&x_{\text{b}}(0)=\frac{1}{2}\left\{-\sqrt{2}\,C_{\text{b}}\cos \phi_{\text{b}}+\sqrt{2}\,C_{\text{c}}\cos\phi_{\text{c}}\right\} =0\\
&\left.\frac{dx_{\text{b}}(t)}{dt}\right|_{t=0}=-\frac{1}{2}\left\{-\sqrt{2}\,C_{\text{b}}\omega_{\text{b}}\sin \phi_{\text{b}}+\sqrt{2}\,C_{\text{c}} \omega_{\text{c}} \sin\phi_{\text{c}}\right\} =0\\
&x_{\text{c}}(0)=\frac{1}{2}\left\{-\sqrt{2}\,C_{\text{a}}\cos\phi_{\text{a}}+C_{\text{b}}\cos\phi_{\text{b}}+ C_{\text{c}}\cos\phi_{\text{c}} \right\}=0 \\
&\left.\frac{dx_{\text{c}}(t)}{dt}\right|_{t=0}=-\frac{1}{2}\left\{-\sqrt{2}\,C_{\text{a}}\omega_{\text{a}}\sin\phi_{\text{a}}+C_{\text{b}}\omega_{\text{b}}\sin\phi_{\text{b}}+C_{\text{c}}\omega_{\text{c}}\sin\phi_{\text{c}} \right\} =0
\end{align}

すなわち

\begin{align}
& \sqrt{2}\,C_{\text{a}}\cos\phi_{\text{a}}+C_{\text{b}}\cos\phi_{\text{b}}+ C_{\text{c}}\cos\phi_{\text{c}}=0 \tag{4-9}\label{iixa0} \\
&\sqrt{2}\,C_{\text{a}}\omega_{\text{a}}\sin\phi_{\text{a}}+C_{\text{b}}\omega_{\text{b}}\sin\phi_{\text{b}}+C_{\text{c}}\omega_{\text{c}}\sin\phi_{\text{c}} =-2V \tag{4-10}\label{iiva0} \\
&-\sqrt{2}\,C_{\text{b}}\cos \phi_{\text{b}}+\sqrt{2}\,C_{\text{c}}\cos\phi_{\text{c}} =0\tag{4-11}\label{iixb0} \\
& -\sqrt{2}\,C_{\text{b}}\omega_{\text{b}}\sin \phi_{\text{b}}+\sqrt{2}\,C_{\text{c}} \omega_{\text{c}} \sin\phi_{\text{c}} =0 \tag{4-12}\label{iivb0}\\
&-\sqrt{2}\,C_{\text{a}}\cos\phi_{\text{a}}+C_{\text{b}}\cos\phi_{\text{b}}+ C_{\text{c}}\cos\phi_{\text{c}}=0 \tag{4-13}\label{iixc0} \\
&-\sqrt{2}\,C_{\text{a}}\omega_{\text{a}}\sin\phi_{\text{a}}+C_{\text{b}}\omega_{\text{b}}\sin\phi_{\text{b}}+C_{\text{c}}\omega_{\text{c}}\sin\phi_{\text{c}} =0 \tag{4-14}\label{iivc0}
\end{align}

　これら(\ref{iixa0})～(\ref{iivc0})を\(C_{\text{a}}, C_{\text{b}} , C_{\text{c}} , \phi_{\text{a}} , \phi_{\text{b}}, \phi_{\text{c}} \)の連立方程式として解くと、\(C_{\text{a}}=V/(\sqrt{2}\,\omega_{\text{a}}),\,\)\(C_{\text{b}}=V/(2\omega_{\text{b}}),\, C_{\text{c}}=V/(2\omega_{\text{c}}),\,\phi_{\text{a}}=\phi_{\text{b}}=\phi_{\text{c}}=-\pi/2\)となる。

　よってこれらを代入すると、

\begin{align}
\begin{cases}
\displaystyle{x_{\text{a}}(t)=\frac{V}{4}\left\{\frac{2}{\omega_{\text{a}}}\cos\left(\omega_{\text{a}} t-\frac{\pi}{2}\right)+\frac{1}{\omega_{\text{b}}}\cos\left(\omega_{\text{b}} t-\frac{\pi}{2}\right) +\frac{1}{\omega_{\text{c}}}\cos\left(\omega_{\text{c}} t-\frac{\pi}{2}\right) \right\}}\\
\displaystyle{x_{\text{b}}(t)=\frac{\sqrt{2}\,V}{4}\left\{-\frac{1}{\omega_{\text{b}}}\cos\left(\omega_{\text{b}} t-\frac{\pi}{2}\right) +\frac{1}{\omega_{\text{c}}}\cos\left(\omega_{\text{c}} t-\frac{\pi}{2}\right) \right\} }\\
\displaystyle{x_{\text{c}}(t)=\frac{V}{4}\left\{-\frac{2}{\omega_{\text{a}}}\cos\left(\omega_{\text{a}} t-\frac{\pi}{2}\right)+\frac{1}{\omega_{\text{b}}}\cos\left(\omega_{\text{b}} t-\frac{\pi}{2}\right) +\frac{1}{\omega_{\text{c}}}\cos\left(\omega_{\text{c}} t-\frac{\pi}{2}\right) \right\} }
\end{cases}\tag{4-15}\label{iikai}
\end{align}

となる。

　

　以上をまとめると

となる。

　

　ここで、(i)、(ii)それぞれの運動について考える。

　(i)は下図のように、両端の2つの球を反対方向に長さ\(L\)だけ移動させてから、手を離して運動させることに相当する。

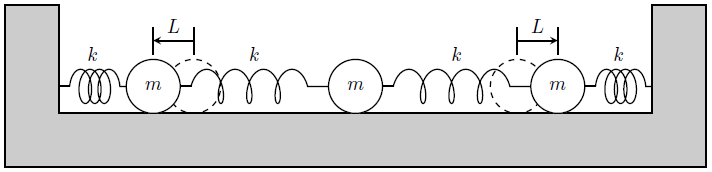
　この場合、両端の2つの球が互いに逆方向の単振動をし、中心の球は運動しないと予想できる。
　そして実際に計算するとその予想通り、両端の2つの球が振幅\(L\)の逆位相の単振動をし、中心の球はその場から動かないことがわかる。

　続いて(ii)だが、これは球aにのみ初速度\(V>0\)を与えて運動させる場合に相当する。
　得られた\( x_{\text{a}}(t) , x_{\text{b}}(t) , x_{\text{c}}(t) \)をグラフにすると下図のようになる。

　球aは初速度を与えられているため、\(t=0\)から傾きを伴って右側へ移動する。
　一方球bと球cは、傾きがない(初速度0の)状態から少しずつ変位が右向きに推移していくことがわかる。

終わりに

　今回はオイラー・ラグランジュ方程式も使って、3つの球の連成振動を扱った。

　球の数が増えても、基本的な解き方は2つの球の場合と変わらないことを示せたと思う。

　次回にもう一問、同じ方法で解ける問題を扱って、力学は一区切りつけようと思う。

　

　END