前回
の続き。
もともと演算回路を取り上げる予定だったが、その前にバーチャルショートをやっておかないといけないことに気づいたのでワンクッション置くことにする。
復習
非反転増幅端子から入る電圧を\(V_\text{in}^{+}\)、反転増幅端子から入る電圧を\(V_\text{in}^{-}\)、開ループゲイン(オペアンプ特有の増幅率)を\(A\)とすると、増幅された出力電圧\(V_{\text{out}}\)は次式で表される。
\begin{align}
V_{\text{out}}=A(V_\text{in}^{+}-V_\text{in}^{-}) \label{opamp1}\tag{1}
\end{align}
またオペアンプを用いた負帰還回路の伝達関数\(V_\text{out}/V_\text{in}^{+}\)は、負帰還の帰還率\(\beta=V_\text{in}^{-}/V_\text{out}\)と開ループゲイン\(A\)の条件\(A\gg 1\)を利用して
\begin{align}
\frac{V_\text{out}}{V_\text{in}^{+}}=\frac{1}{\frac{1}{A}+\beta}\simeq\frac{1}{\beta} \label{伝達関数}\tag{2}
\end{align}
となる。

バーチャルショートとは
ここでもう一度、オペアンプの入力電圧と出力電圧の関係(\ref{opamp1})をよく見てみよう。
\begin{align}
V_{\text{out}}=A(V_\text{in}^{+}-V_\text{in}^{-}) \tag{1}
\end{align}
多くのオペアンプでは開ループゲイン\(A\gg 1\)であり、理想は無限大である。
もし\(A\)が無限大なら、(\ref{opamp1})よりオペアンプの出力電圧\(V_{\text{out}}\)は0か\(\pm\infty\)のいずれかになるはずだ。
しかし実際は、\(V_{\text{out}}\)は有限の値をとる。
\(A\)が無限大でも、\(V_{\text{out}}\)が有限値を取るにはどうすればよいか。
ここでもう一度(\ref{opamp1})に立ち返ると、右辺の\(V_\text{in}^{+}-V_\text{in}^{-}\)が限りなく小さい値を取れば、\(V_{\text{out}}\)が有限値を取ることがわかる。
言い換えれば\(V_\text{in}^{+}-V_\text{in}^{-}\)がほぼ0、すなわち非反転入力端子の電圧\(V_\text{in}^{+}\)と反転入力端子の電圧\(V_\text{in}^{-}\)がほぼ同じであれば良い。
電圧が同じということは、短絡(ショート)しているということになる。
しかし、もちろん実際のオペアンプでは2つの入力端子はショートしておらず、この結果は両者がショートしているとみなせるということを示している過ぎない。
これをバーチャルショート(イマジナリーショート、仮想短絡)と呼ぶ。
バーチャルショート
\begin{align}
V_\text{in}^{+}=V_\text{in}^{-} \label{バーチャルショート}\tag{2}
\end{align}
このバーチャルショートを使うと、オペアンプの負帰還回路の伝達関数をより簡単に導出することができるようになる。
例
前回扱った回路に実際にバーチャルショートを適用してみる。
ただしオペアンプの入力インピーダンスは無限大とみなす。
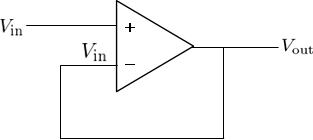
ボルテージフォロワ
ボルテージフォロワにバーチャルショートを適用すると図2のようになる。
よって
\begin{align}
\boxed{\frac{V_{\text{out}}}{V_{\text{in}}}=1}
\end{align}
となり、直接伝達関数を求めることができる。
非反転増幅回路
非反転増幅回路にバーチャルショートを適用すると図3のようになる。
よって抵抗\(R_{1}\)に流れる電流を\(i\)とすると、オームの法則より
\begin{align}
&V_{\text{out}}-V_{\text{in}}=iR_{1}\label{非反転1}\tag{3}\\
&V_{\text{in}}=iR_{2}\label{非反転2}\tag{4}\\
\end{align}
となる。
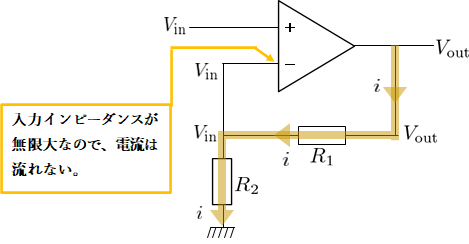
よって(\ref{非反転1})と(\ref{非反転2})より
\begin{align}
\boxed{\frac{V_{\text{out}}}{V_{\text{in}}}=1+\frac{R_{1}}{R_{2}}}
\end{align}
となり、オームの法則から直接伝達関数を求めることができる。
反転増幅回路
反転増幅回路では非反転入力端子が接地されているため、バーチャルショートを適用すると2つの入力端子の電圧がともに\(0\,\text{V}\)になる(図4)。
よって抵抗\(R_{1}\)に流れる電流を\(i\)とすると、オームの法則より
\begin{align}
&V_{\text{in}}-0=iR_{1}\label{反転1}\tag{5}\\
&0-V_{\text{out}}=iR_{2}\label{反転2}\tag{6}\\
\end{align}
となる。

よって(\ref{反転1})と(\ref{反転2})より
\begin{align}
\boxed{\frac{V_{\text{out}}}{V_{\text{in}}}=-\frac{R_{2}}{R_{1}}}
\end{align}
となり、こちらもオームの法則から直接伝達関数を求めることができる。
終わりに
これで準備は整った。
今度こそ次回は、演算回路を取り上げていく。
次回はこちら。




コメント