前回
の続き。
今回は前々回
に取り上げたオペアンプの基本回路の応用である演算回路を見ていく。
各回路の伝達関数の導出には、前回取り上げたバーチャルショートが大いに役立つ。
まずは加算回路と減算回路(差動回路)の2つから。
加算回路
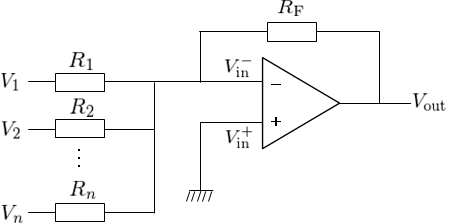
右図のように、反転増幅回路の入力側の抵抗の数を並列接続で増やした回路を考える。
この回路の出力電圧\(V_{\text{out}}\)は各入力電圧\(V_{k}\,(k=1,2,…,n)\)を利用して、
\begin{align}
V_{\text{out}}=-R_{\text{F}}\sum_{k=1}^{n}\frac{V_{k}}{R_{k}}\label{加算1}\tag{1}
\end{align}
と表せられる。
ここで\(R_{1}=R_{2}=…=R_{n}=R_{\text{F}}=R\)とし、回路の抵抗値を全て揃えると
\begin{align}
V_{\text{out}}=-\sum_{k=1}^{n}V_{k} \label{加算2}\tag{2}
\end{align}
となり、入力電圧の総和が反転されて出力される。
入力電圧を足し上げる回路であるため、この回路を加算回路(反転加算回路)と呼ぶ。
問題1
加算回路の出力電圧(\ref{加算1})をバーチャルショートを利用して導出せよ。
ただし、オペアンプの入力インピーダンスを無限大としてよい。
解答
\(k=0,1,…,n\)とする。
加算回路では非反転入力端子が接地されているため、バーチャルショートを適用すると2つの入力端子の電圧がともに\(0\,\text{V}\)になる(図2)。
抵抗\(R_{k}\)に流れる電流を\(i_{k}\)とすると、オームの法則より
\begin{gather}
V_{k}-0=i_{k}R_{k}\\
\therefore i_{k}=\frac{V_{k}}{R_{k}}\label{加算3}\tag{3}
\end{gather}
となる。
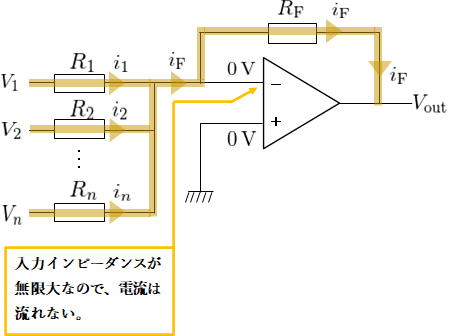
さらにキルヒホッフの法則より、反転入力端子へと向かう電流\(i_{\text{F}}\)は
\begin{align}
i_{\text{F}}=\sum_{k=1}^{n}i_{k}\label{加算4}\tag{4}
\end{align}
となる。
ここでオペアンプの入力インピーダンスは無限大であるため、反転入力端子に電流\(i_{\text{F}}\)は流れず、すべて抵抗\(R_{\text{F}}\)に流れる。
よってオームの法則より
\begin{align}
0-V_{\text{out}}=i_{\text{F}}R_{\text{F}}\quad \therefore V_{\text{out}}=-i_{\text{F}}R_{\text{F}} \label{加算5}\tag{5}
\end{align}
となる。
よって(\ref{加算3})~(\ref{加算5})より
\begin{align}
V_{\text{out}}=-R_{\text{F}}\sum_{k=1}^{n}i_{k}=-R_{\text{F}}\sum_{k=1}^{n}\frac{V_{k}}{R_{k}}\quad\therefore V_{\text{out}}=-R_{\text{F}}\sum_{k=1}^{n}\frac{V_{k}}{R_{k}}
\end{align}
となり(\ref{加算1})を導出できる。
減算回路(差動回路)
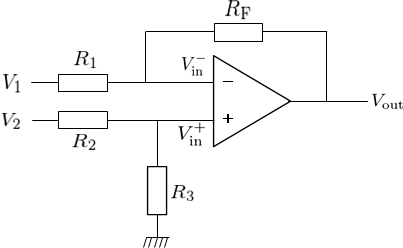
反転増幅回路の非反転入力端子側に2つの抵抗を並列に接続する。
2つの抵抗のうちの片方からは電圧を入力し、もう片方は接地する(図3)。
このとき、この回路の出力電圧\(V_{\text{out}}\)は入力電圧\(V_{1},\,V_{2}\)を利用して、
\begin{align}
V_{\text{out}}=-\frac{R_{\text{F}}}{R_{1}}V_{1}+\left(1+\frac{R_{\text{F}}}{R_{1}}\right)\frac{R_{3}}{R_{2}+R_{3}}V_{2}\label{減算1}\tag{6}
\end{align}
と表せられる。
ここで\(R_{1}=R_{2}=R_{3}=R_{\text{F}}=R\)とし、回路の抵抗値を全て揃えると
\begin{align}
V_{\text{out}}=V_{2}-V_{1} \label{減算2}\tag{7}
\end{align}
となり、2つの入力電圧の差が出力される。
入力電圧の差を出力する回路であるため、この回路を減算回路(差動回路、差動増幅回路)と呼ぶ。
問題2
減算回路の出力電圧(\ref{減算1})をバーチャルショートを利用して導出せよ。
ただし、オペアンプの入力インピーダンスを無限大としてよい。
解答
バーチャルショートを適用し、2つの入力端子の電圧をともに\(V_{\text{in}}\)とする(図4)。
抵抗\(R_{1}\)を流れる電流を\(i_{1}\)、抵抗\(R_{2}\)を流れる電流を\(i_{2}\)とすると、オームの法則より
\begin{gather}
V_{1}-V_{\text{in}}=i_{1}R_{1} \label{減算3}\tag{8}\\
V_{2}-V_{\text{in}}=i_{2}R_{2} \label{減算4}\tag{9}\\
\end{gather}
となる。
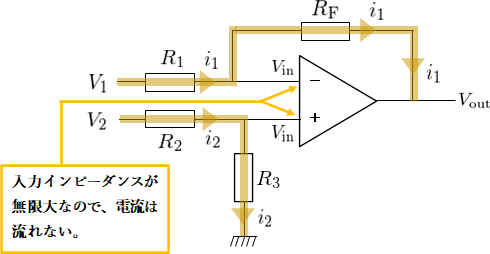
ここでオペアンプの入力インピーダンスは無限大であるため、電流\(i_{1}\)は反転入力端子には流れず抵抗\(R_{\text{F}}\)に流れ、電流\(i_{2}\)は非反転入力端子には流れず抵抗\(R_{\text{3}}\)に流れる。
よってオームの法則より
\begin{gather}
V_{\text{in}}-V_{\text{out}}=i_{1}R_{\text{F}}\label{減算5}\tag{10}\\
V_{\text{in}}-0=i_{2}R_{3}\label{減算6}\tag{11}
\end{gather}
となる。
よって(\ref{減算3})と(\ref{減算5})から\(i_{1}\)を消去すると
\begin{align}
V_{\text{in}}-V_{\text{out}}=\frac{V_{1}-V_{\text{in}}}{R_{1}}R_{\text{F}}\label{減算7}\tag{12}
\end{align}
となり、(\ref{減算4})と(\ref{減算6})から\(i_{2}\)を消去すると
\begin{align}
V_{2}-V_{\text{in}}=\frac{V_\text{in}}{R_{3}}R_{2}\label{減算8}\tag{13}
\end{align}
となるため、(\ref{減算7})と(\ref{減算8})から\(V_{\text{in}}\)を消去して整理すると
\begin{align}
V_{\text{out}}=-\frac{R_{\text{F}}}{R_{1}}V_{1}+\left(1+\frac{R_{\text{F}}}{R_{1}}\right)\frac{R_{3}}{R_{2}+R_{3}}V_{2}
\end{align}
が得られ、(\ref{減算1})を導出できる。
終わりに
ここまでの回路では、オペアンプ以外の素子は抵抗のみだった。
次回は、抵抗に加えてコンデンサを利用した演算回路である微分回路と積分回路を取り上げる。
次回はこちら。




コメント