複雑な回路を解析する際、キルヒホッフの法則を逐一立てて連立方程式を解く方法は時間がかかる。
しかし、連立方程式を行列表示することができれば見通し良く解析することができる。
本記事では、この行列表示を利用する2つの閉回路の解析手法について紹介する。
まずは閉路解析から。
概要
まずは閉路解析(網目解析、メッシュ解析)について見てく。
これは回路内の閉路(網目)に着目して解析する手法である。
手順は下記の通り。
- 回路内にある閉路をすべて列挙し、閉路内に流れる電流(閉路電流)の向きを決める。
- 列挙した閉路の数を\(n\)とし、\(n\times n\)の行列\(\mathsf{Z}\)を下記のように立てる。
(1)対角成分に閉路内にある素子のインピーダンスの総和を入れる。
(2)非対角成分に2つの閉路に共通する素子のインピーダンスを符号を反転させて入れる。
\begin{align}&\qquad\qquad\;\;\boxed{\begin{matrix}1\quad\, & 2 \quad\, &\cdots &n\end{matrix}}\notag \\&\mathsf{Z}=\boxed{\begin{matrix}1\\2\\ \vdots \\ n\end{matrix}}\begin{pmatrix}Z_{1,1}&Z_{1,2}&\cdots&Z_{1,n}\\Z_{2,1}&Z_{2,2}&\cdots&Z_{2,n}\\\vdots&\vdots&\ddots&\vdots\\Z_{n,1}&Z_{n,2}&\cdots&Z_{n,n}\end{pmatrix} \\ &\begin{cases}Z_{k,k}(k=1,2,…,n):\text{閉路}k\text{内にある素子のインピーダンスの総和}\\Z_{i,j}=Z_{j,i}(i\neq j):\text{閉路}i,j\text{に共通する素子のインピーダンスの符号反転値}\end{cases}\end{align} - 閉路電流を並べた縦ベクトル\(\vec{I}\)に行列\(\mathsf{Z}\)をかける。
ただし閉路内に電流源がある場合は、対応するベクトルの成分を電流源の電流値と同値にする。
符号は閉路電流の向きと同じなら正、逆なら負とする。
\begin{align}\mathsf{Z}\vec{I}=\begin{pmatrix}Z_{1,1}&Z_{1,2}&\cdots&Z_{1,n}\\Z_{2,1}&Z_{2,2}&\cdots&Z_{2,n}\\\vdots&\vdots&\ddots&\vdots\\Z_{n,1}&Z_{n,2}&\cdots&Z_{n,n}\end{pmatrix}\begin{pmatrix}i_{1}\\i_{2}\\ \vdots \\i_{n}\end{pmatrix}\quad i_{k}(k=1,2,…,n):\text{閉路電流}\end{align} - 閉路内の電圧源が印加する電圧を並べた縦ベクトル\(\vec{E}\)を\(\mathsf{Z}\vec{I}\)と等号で結ぶ。
符号は、電圧源の正極から負極に向かう向きが閉路電流の向きと同じなら正、逆なら負とする。
ただし閉路内に電流源がある場合は、形式的に電流源を電圧源とみなし、対応するベクトルの成分に形式的に電流源の電圧を入れる。
符号は、電流源の電流が閉路電流の向きと同じなら正、逆なら負とする。
\begin{align}&\mathsf{Z}\vec{I}=\vec{E}\notag \\&\begin{pmatrix}Z_{1,1}&Z_{1,2}&\cdots&Z_{1,n}\\Z_{2,1}&Z_{2,2}&\cdots&Z_{2,n}\\\vdots&\vdots&\ddots&\vdots\\Z_{n,1}&Z_{n,2}&\cdots&Z_{n,n}\end{pmatrix}\begin{pmatrix}i_{1}\\i_{2}\\ \vdots \\i_{n}\end{pmatrix}=\begin{pmatrix}E_{1}\\E_{2}\\ \vdots \\E_{n}\end{pmatrix}\notag \\&E_{k}(k=1,2,…,n):\text{閉路}k\text{内の電圧源が印加する電圧}\end{align} - 方程式\(\mathsf{Z}\vec{I}=\vec{E}\)を解く。
方程式\(\mathsf{Z}\vec{I}=\vec{E}\)を網目方程式(メッシュ方程式)と呼び、行列\(\mathsf{Z}\)をループ・インピーダンス行列と呼ぶ。
ここでは\(\vec{I}\)が未知の行列であるため、\(\mathsf{Z}\)の逆行列\(\mathsf{Z}^{-1}\)を求めることができれば\(\vec{I}=\mathsf{Z}^{-1}\vec{E}\)となって\(\vec{I}\)を求めることができる。
例題1
上述の解説だけではイメージが掴めないと思うので、例題を交えて実際の使い方を見ていく。
例題1
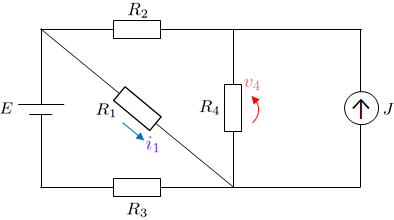
図1の回路の抵抗\(R_{1}\)に流れる電流\(i_{1}\)、抵抗\(R_{4}\)にかかる電圧\(v_{4}\)を閉路解析を利用してそれぞれ求めよ。
ただし\(E\)は直流電圧源、\(J\)は直流電流源であり、\(R_{k}=2\,\Omega(k=1,2,3,4),\,E=24\,\text{V},\,J=1\,\text{A}\)である。
また\(v_{4}\)については矢印の向きとは逆向きに電圧降下があるとする。
解答
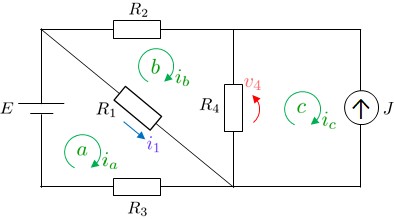
回路内には閉路が3つ存在する。
それぞれ\(a,b,c\)とし、各閉路を流れる電流(閉路電流)の向きをすべて時計回りに取る(図2参照)。
閉路は3つなので、\(3\times 3\)のループ・インピーダンス行列\(\mathsf{Z}\)を立てる。
まず、各閉路と\(\mathsf{Z}\)の行と列を次式のように紐づけする。
\begin{align}
&\quad\,\boxed{\begin{matrix}a\quad\, & b \quad\, &c\end{matrix}}\notag \\
\mathsf{Z}=\boxed{\begin{matrix}a\\b\\c\end{matrix}}
&\begin{pmatrix}Z_{1,1}&Z_{1,2}&Z_{1,3}\\
Z_{2,1}&Z_{2,2}&Z_{2,3}\\
Z_{3,1}&Z_{3,2}&Z_{3,3}
\end{pmatrix}
\end{align}
次に、各閉路内にある素子のインピーダンスの総和を、各閉路で紐づけされた対角成分に入れる。
例えば\(Z_{1,1}\)には閉路\(a\)が紐づけされているので、閉路\(a\)内にある素子のインピーダンスの総和を\(Z_{1,1}\)に入れる。
\begin{align}
&\quad\quad\boxed{\begin{matrix}a\qquad\qquad\, & b \qquad\qquad &c\end{matrix}}\notag \\
\mathsf{Z}=\boxed{\begin{matrix}a\\b\\c\end{matrix}}
&\begin{pmatrix}R_{1}+R_{3}&Z_{1,2}&Z_{1,3}\\
Z_{2,1}&R_{1}+R_{2}+R_{4}&Z_{2,3}\\
Z_{3,1}&Z_{3,2}&R_{4}
\end{pmatrix}
\end{align}
次に、2つの閉路に共通する素子のインピーダンスを、各閉路で紐づけされた非対角成分に符号を反転させて入れる。
例えば\(Z_{1,2},\,Z_{2,1}\)には、閉路\(a,b\)に共通する素子である\(R_{1}\)を符号を反転させて入れる。
\begin{align}
&\quad\quad\boxed{\begin{matrix}a\qquad\qquad\, & b \qquad\qquad &c\end{matrix}}\notag \\
\mathsf{Z}=\boxed{\begin{matrix}a\\b\\c\end{matrix}}&\begin{pmatrix}R_{1}+R_{3}&-R_{1}&0\\
-R_{1}&R_{1}+R_{2}+R_{4}&-R_{4}\\
0&-R_{4}&R_{4}
\end{pmatrix}
\end{align}
これで\(\mathsf{Z}\)は完成である。
続いて、閉路電流を並べた縦ベクトル\(\vec{I}\)を立てる。成分を並べる順番は、\(\mathsf{Z}\)に則る。
\begin{align}
\vec{I}=\begin{pmatrix}i_{a}\\ i_{b}\\i_{c}\end{pmatrix}=\begin{pmatrix}i_{a}\\ i_{b}\\-J\end{pmatrix}
\end{align}
今回は閉路\(c\)に電流源\(J\)があるため、電流の向きに留意して\(i_{c}=-J\)とする。
続いて、閉路内の電圧源が印加する電圧を並べた縦ベクトル\(\vec{E}\)を立てる。成分を並べる順番は、\(\mathsf{Z}\)に則る。
\begin{align}
\vec{E}=\begin{pmatrix}E\\0\\-E_{J}\end{pmatrix}
\end{align}
閉路\(a\)には電圧源\(E\)があり、閉路電流\(i_{a}\)は電圧源\(E\)の正極から負極へ向かう向きに流れているので符号は正となる。
また、閉路\(c\)には電流源\(J\)があるため、形式的に電流源\(J\)を電圧源\(E_{J}\)とみなす。
電流源から流れる電流の向きが閉路電流\(i_{c}\)の向きと逆であるため、符号は負となる。
よって\(\mathsf{Z}\vec{I}\)と\(\vec{E}\)を等号で結べば網目方程式が完成する。
\begin{gather}
\mathsf{Z}\vec{I}=\vec{E} \notag \\
\begin{pmatrix}R_{1}+R_{3}&-R_{1}&0\\
-R_{1}&R_{1}+R_{2}+R_{4}&-R_{4}\\
0&-R_{4}&R_{4}
\end{pmatrix}\begin{pmatrix}i_{a}\\ i_{b}\\-J\end{pmatrix}=\begin{pmatrix}E\\0\\-E_{J}\end{pmatrix}
\end{gather}
ここで値を代入すると
\begin{align}
\begin{pmatrix}4&-2&0\\
-2&6&-2\\
0&-2&2
\end{pmatrix}\begin{pmatrix}i_{a}\\ i_{b}\\-1\end{pmatrix}=\begin{pmatrix}24\\0\\-E_{J}\end{pmatrix}\label{閉路解析例式1}\tag{1}
\end{align}
となる。
求めるべき未知量が\(i_{a},i_{b}\)の2つとなったため、(\ref{閉路解析例式1})を次のように簡素化する。
\begin{align}
\begin{pmatrix}4&-2\\ -2&6\end{pmatrix}\begin{pmatrix}i_{a}\\ i_{b}\end{pmatrix}=\begin{pmatrix}24\\ -2\end{pmatrix}\label{閉路解析例式2}\tag{2}
\end{align}
(\ref{閉路解析例式2})を解くと、
\begin{align}
\begin{pmatrix}i_{a}\\ i_{b}\end{pmatrix}&=\begin{pmatrix}4&-2\\ -2&6\end{pmatrix}^{-1}\begin{pmatrix}24\\ -2\end{pmatrix} \notag \\
&=\frac{1}{24-4}\begin{pmatrix}6&2\\ 2&4\end{pmatrix}\begin{pmatrix}24\\ -2\end{pmatrix}\notag \\
&=\frac{1}{5}\begin{pmatrix}3&1\\ 1&2\end{pmatrix}\begin{pmatrix}12\\ -1\end{pmatrix}=\begin{pmatrix}7\\ 2\end{pmatrix}\label{閉路解析例式3}\tag{3}
\end{align}
となる。
最後に(\ref{閉路解析例式3})の結果から\(i_{1},v_{4}\)を求める。
\(i_{1}\)については、\(i_{1}\)と同方向に\(i_{a}\)、逆方向に\(i_{b}\)が\(R_{1}\)に流れているため、
\begin{align}
i_{1}=i_{a}-i_{b}=7-2=5\,\text{A}
\end{align}
となる。
また\(v_{4}\)については、矢印とは逆向きに電圧降下があるとしているため、\(R_{4}\)を流れる電流は\(i_{b}\)と同じ向きを取る。
よって\(R_{4}\)には\(i_{b}\)、およびそれとは逆向きに\(i_{c}=-J=-1\,\text{A}\)が流れているため、
\begin{align}
v_{4}=(i_{b}-i_{c})R_{4}=(2+1)\times 2=6\,\text{V}
\end{align}
となる。
以上より\(\boxed{i_{1}=5\,\text{A},\,v_{4}=6\,\text{V}}\)となる。
例題2
例題2
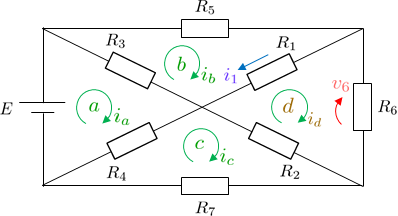
図3の回路の抵抗\(R_{1}\)に流れる電流\(i_{1}\)、抵抗\(R_{6}\)にかかる電圧\(v_{6}\)を閉路解析を利用してそれぞれ求めよ。
ただし\(E\)は直流電圧源であり、\(R_{1,2}=1\,\Omega,\,R_{3,4,5,6,7}=2\,\Omega,\,E=10\,\text{V}\)である。
また\(v_{6}\)については矢印の向きとは逆向きに電圧降下があるとする。

解説
回路内には閉路が4つ存在する。
それぞれ\(a,b,c,d\)とし、各閉路を流れる電流(閉路電流)の向きをすべて時計回りに取る(図4参照)。
閉路は4つなので、\(4\times 4\)のループ・インピーダンス行列\(\mathsf{Z}\)を立てる。
まず、各閉路と\(\mathsf{Z}\)の行と列を次式のように紐づけする。
\begin{align}
&\quad\,\boxed{\begin{matrix}a\quad\, & b \quad\,\, &c\quad\,\,&d\end{matrix}}\notag \\
\mathsf{Z}=\boxed{\begin{matrix}a\\b\\c\\d\end{matrix}}&\begin{pmatrix}Z_{1,1}&Z_{1,2}&Z_{1,3}&Z_{1,4}\\
Z_{2,1}&Z_{2,2}&Z_{2,3}&Z_{2,4}\\
Z_{3,1}&Z_{3,2}&Z_{3,3}&Z_{3,4}\\
Z_{4,1}&Z_{4,2}&Z_{4,3}&Z_{4,4}
\end{pmatrix}
\end{align}
次に、各閉路内にある素子のインピーダンスの総和を、各閉路で紐づけされた対角成分に入れる。
例えば\(Z_{1,1}\)には閉路\(a\)が紐づけされているので、閉路\(a\)内にある素子のインピーダンスの総和を\(Z_{1,1}\)に入れる。
\begin{align}
&\quad\quad\boxed{\begin{matrix}a\qquad\qquad\,\, & b \qquad\qquad\quad\quad &c\qquad\qquad\quad&d\end{matrix}}\notag \\
\mathsf{Z}=\boxed{\begin{matrix}a\\b\\c\\d\end{matrix}}&\begin{pmatrix}R_{3}+R_{4}&Z_{1,2}&Z_{1,3}&Z_{1,4}\\
Z_{2,1}&R_{1}+R_{3}+R_{5}&Z_{2,3}&Z_{2,4}\\
Z_{3,1}&Z_{3,2}&R_{2}+R_{4}+R_{7}&Z_{3,4}\\
Z_{4,1}&Z_{4,2}&Z_{4,3}&R_{1}+R_{2}+R_{6}
\end{pmatrix}
\end{align}
次に、2つの閉路に共通する素子のインピーダンスを、各閉路で紐づけされた非対角成分に符号を反転させて入れる。
例えば\(Z_{1,2},\,Z_{2,1}\)には、閉路\(a,b\)に共通する素子である\(R_{1}\)を符号を反転させて入れる。
\begin{align}
&\quad\quad\boxed{\begin{matrix}a\qquad\qquad\,\, & b \qquad\qquad\quad\quad &c\qquad\qquad\quad&d\end{matrix}}\notag \\
\mathsf{Z}=\boxed{\begin{matrix}a\\b\\c\\d\end{matrix}}&\begin{pmatrix}R_{3}+R_{4}&-R_{3}&-R_{4}&0\\
-R_{3}&R_{1}+R_{3}+R_{5}&0&-R_{1}\\
-R_{4}&0&R_{2}+R_{4}+R_{7}&-R_{2}\\
0&-R_{1}&-R_{2}&R_{1}+R_{2}+R_{6}
\end{pmatrix}
\end{align}
これで\(\mathsf{Z}\)は完成である。
続いて、閉路電流を並べた縦ベクトル\(\vec{I}\)を立てる。
成分を並べる順番は、\(\mathsf{Z}\)に則る。
\begin{align}
\vec{I}=\begin{pmatrix}i_{a}\\ i_{b}\\i_{c}\\ i_{d}\end{pmatrix}
\end{align}
続いて、閉路内の電圧源が印加する電圧を並べた縦ベクトル\(\vec{E}\)を立てる。
成分を並べる順番は、\(\mathsf{Z}\)に則る。
\begin{align}
\vec{E}=\begin{pmatrix}E\\0\\0\\0\end{pmatrix}
\end{align}
閉路\(a\)には電圧源\(E\)があり、閉路電流\(i_{a}\)は電圧源\(E\)の正極から負極へ向かう向きに流れているので符号は正となる。
よって\(\mathsf{Z}\vec{I}\)と\(\vec{E}\)を等号で結べば網目方程式が完成する。
\begin{gather}
\mathsf{Z}\vec{I}=\vec{E} \notag \\
\begin{pmatrix}R_{3}+R_{4}&-R_{3}&-R_{4}&0\\
-R_{3}&R_{1}+R_{3}+R_{5}&0&-R_{1}\\
-R_{4}&0&R_{2}+R_{4}+R_{7}&-R_{2}\\
0&-R_{1}&-R_{2}&R_{1}+R_{2}+R_{6}
\end{pmatrix}\begin{pmatrix}i_{a}\\ i_{b}\\i_{c}\\ i_{d}\end{pmatrix}=\begin{pmatrix}E\\0\\0\\0\end{pmatrix}
\end{gather}
ここで値を代入すると
\begin{align}
\begin{pmatrix}4&-2&-2&0\\
-2&5&0&-1\\
-2&0&5&-1\\
0&-1&-1&4
\end{pmatrix}\begin{pmatrix}i_{a}\\ i_{b}\\i_{c}\\ i_{d}\end{pmatrix}=\begin{pmatrix}10\\0\\0\\0\end{pmatrix}\label{閉路解析例式2-1}\tag{4}
\end{align}
となる。
(\ref{閉路解析例式2-1})を解くと
\begin{align}
\begin{pmatrix}i_{a}\\ i_{b}\\i_{c}\\ i_{d}\end{pmatrix}&=\begin{pmatrix}4&-2&-2&0\\
-2&5&0&-1\\
-2&0&5&-1\\
0&-1&-1&4
\end{pmatrix}^{-1}\begin{pmatrix}10\\0\\0\\0\end{pmatrix} \notag \\
&=\frac{1}{20}\begin{pmatrix}
9&4&4&2\\
4&6&2&2\\
4&2&6&2\\
2&2&2&6
\end{pmatrix}\begin{pmatrix}10\\0\\0\\0\end{pmatrix}\notag \\
&=\frac{1}{2}\begin{pmatrix}
9&4&4&2\\
4&6&2&2\\
4&2&6&2\\
2&2&2&6
\end{pmatrix}\begin{pmatrix}1\\0\\0\\0\end{pmatrix}=\begin{pmatrix}4.5\\2\\2\\1\end{pmatrix}\label{閉路解析例式2-2}\tag{5}
\end{align}
となる。
最後に(\ref{閉路解析例式2-2})の結果から\(i_{1},v_{6}\)を求める。
\(i_{1}\)については、\(i_{1}\)と同方向に\(i_{b}\)、逆方向に\(i_{d}\)が\(R_{1}\)に流れているため、
\begin{align}
&i_{1}=i_{b}-i_{d}=2-1=1\,\text{A}
\end{align}
となる。
また\(v_{6}\)については、矢印とは逆向きに電圧降下があるとしているため、\(R_{6}\)を曲がれる電流の向きは\(i_{d}\)と一致する。
\begin{align}
v_{6}=i_{d}R_{6}=1\times 2=2\,\text{V}
\end{align}
となる。
以上より\(\boxed{i_{1}=1\,\text{A},\,v_{4}=2\,\text{V}}\)となる。
終わりに
今回は閉回路の閉路に着目したが、次回は閉回路の節点に着目した節点解析を扱う。
続きはこちら。
END





コメント