前回
の続き。
今回は3次の正方行列のディターミナントと逆行列について見ていく。
3次の正方行列の逆行列
さて、次は3次の正方行列の逆行列だが、こちらは2次の正方行列とは全く違う方法で求める。
これは具体的な行列を使った方がわかりやすいので、次の行列について考えることにする。
\begin{align}
\mathsf{A}=\begin{pmatrix}
3&0&2\\
9&4&4\\
0&1&0
\end{pmatrix}
\end{align}
まず、行列\(\mathsf{A}\)が正則かどうかディターミナントを計算して確かめなければならない。
3次の正方行列のディターミナントは次のようにして求める。
3次の正方行列のディターミナントの求め方
① 下図のたすき掛けの要領で3つの成分の掛け算を3つ実行し、それらを足し上げる。
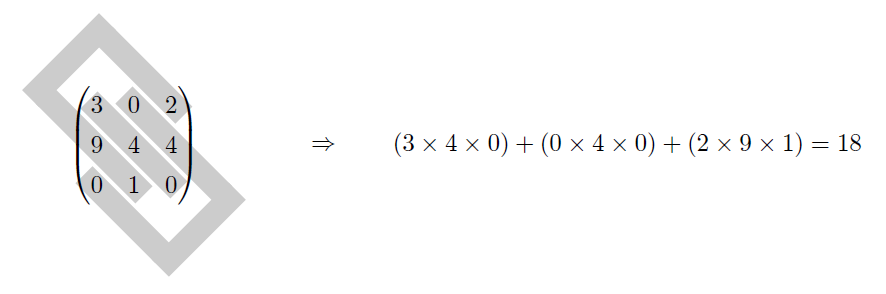
② 下図のたすき掛けの要領で3つの成分の掛け算を3つ実行し、それらを足し上げる。
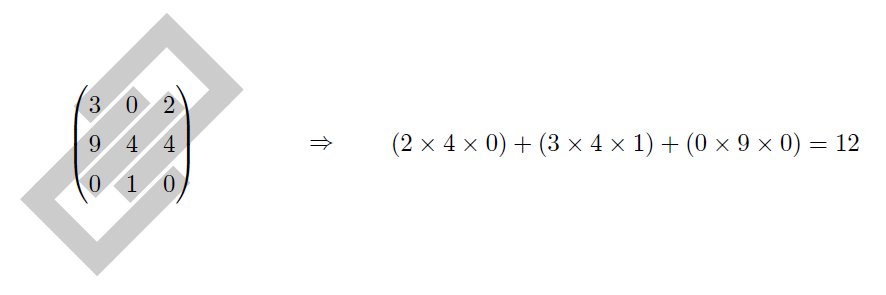
③ ①で得られた結果から②で得られた結果を引くと、それが\(\text{det}[\mathsf{A}]\)となる。
\begin{align}
\text{det}[\mathsf{A}]=18-12=6
\end{align}
よって行列\(\mathsf{A}\)は正則であり、逆行列が存在することがわかった。
これで心置きなく、逆行列を求められる。
逆行列の求め方自体は複数あるが、今回は行列の成分の数が多い場合に使われるガウスの消去法を使う。
3次の正方行列の逆行列の求め方(ガウスの消去法)
① 元の行列の右隣に単位行列を並べ、下記のように両者を縦線で区切る。
\begin{align}
\left(\begin{array}{ccc|ccc}
3&0&2&1&0&0 \\
9&4&4&0&1&0 \\
0&1&0&0&0&1
\end{array}\right)
\end{align}
② 下記3つの操作を順次実行し、左側のもとの行列が単位行列になるようにする。
(1) 2つの行を入れ替える。
(2) ある行を定数倍したものを、他の行に加える(あるいは引く)。
(3) ある行を定数倍する。
例の行列の場合は下記のように実行する。
\left(\begin{array}{ccc|ccc}
3&0&2&1&0&0 \\
0&1&0&0&0&1 \\
9&4&4&0&1&0
\end{array}\right)
\end{align}
\left(\begin{array}{ccc|ccc}
3&0&2&1&0&0 \\
0&1&0&0&0&1 \\
0&4&-2&-3&1&0
\end{array}\right)
\end{align}
\left(\begin{array}{ccc|ccc}
3&0&2&1&0&0 \\
0&1&0&0&0&1 \\
0&0&-2&-3&1&-4
\end{array}\right)
\end{align}
\left(\begin{array}{ccc|ccc}
3&0&0&-2&1&-4 \\
0&1&0&0&0&1 \\
0&0&-2&-3&1&-4
\end{array}\right)
\end{align}
\left(\begin{array}{ccc|ccc}
1&0&0&-2/3&1/3&-4/3 \\
0&1&0&0&0&1 \\
0&0&1&3/2&-1/2&2
\end{array}\right)
\end{align}
③ ②の計算で最終的に右側に現れた行列が、求める逆行列になる。
\begin{align}
\mathsf{A}^{-1}=\frac{1}{6}\begin{pmatrix}
-4&2&-8\\
0&0&6\\
9&-3&12
\end{pmatrix}
\end{align}
ガウスの消去法は任意のd次の正方行列に対して適用でき、予めディターミナントを求めることなく逆行列を求められる。
しかし、行列が正則でない場合にガウスの消去法で逆行列を求めようとしても、逆行列は永遠に求められない。
問題文に明示されていれば話は別だが、そうでない場合は予めディターミナントを求めておき、行列が正則か否か確認しておいた方が良いだろう。
練習問題
次の行列\(\mathsf{A},\mathsf{B}\)が正則か否かを調べた上で、その逆行列を求めよ。
\begin{align}
\mathsf{A}=\begin{pmatrix}
2&0&3\\
4&4&1\\
0&2&0
\end{pmatrix}
\qquad\qquad\mathsf{B}=\begin{pmatrix}
-2&3&-6\\
0&0&5\\
4&-6&4
\end{pmatrix}
\end{align}
解答
まず行列\(\mathsf{A}\)について、ディターミナントを計算すると
\begin{align}
\text{det}[\mathsf{A}]&=(2\times4\times0)+(0\times1\times0)+(3\times4\times2)-(3\times4\times0)-(2\times1\times2)-(0\times4\times0)\\
&=24-4=20
\end{align}
となり、行列\(\mathsf{A}\)は正則であるから逆行列が存在する。
よってガウスの消去法で逆行列を求めると、
\left(\begin{array}{ccc|ccc}
2&0&3&1&0&0 \\
4&4&1&0&1&0 \\
0&2&0&0&0&1
\end{array}\right)
\end{align}
\left(\begin{array}{ccc|ccc}
2&0&3&1&0&0 \\
0&2&0&0&0&1 \\
4&4&1&0&1&0
\end{array}\right)
\end{align}
\left(\begin{array}{ccc|ccc}
2&0&3&1&0&0 \\
0&2&0&0&0&1 \\
0&4&-5&-2&1&0
\end{array}\right)
\end{align}
\left(\begin{array}{ccc|ccc}
2&0&3&1&0&0 \\
0&2&0&0&0&1 \\
0&0&-5&-2&1&-2
\end{array}\right)
\end{align}
\left(\begin{array}{ccc|ccc}
2&0&0&-1/5&3/5&-6/5 \\
0&2&0&0&0&1 \\
0&0&-5&-2&1&-2
\end{array}\right)
\end{align}
\left(\begin{array}{ccc|ccc}
1&0&0&-1/10&3/10&-3/5 \\
0&1&0&0&0&1/2 \\
0&0&1&2/5&-1/5&2/5
\end{array}\right)
\end{align}
よって逆行列は次のように求められる。
\begin{align}
\mathsf{A}^{-1}=\frac{1}{10}\begin{pmatrix}-1&3&-6\\0&0&5\\4&-2&4\end{pmatrix}
\end{align}
続いて行列\(\mathsf{B}\)だが、ディターミナントを計算すると
\begin{align}
\text{det}[\mathsf{B}]=0+(3\times5\times4)+0-0-\{(-2)\times5\times(-6)\}-0=60-60=0
\end{align}
となり、行列\(\mathsf{B}\)は正則ではない。
よって、行列\(\mathsf{B}\)には逆行列が存在しないことがわかる。
注意点と次回予告
今後は基本的に2次および3次の正方行列しか扱わないので、今回の内容がマスターできれば逆行列とディターミナントは問題ない。
両方に共通する注意事項としては
① ディターミナントを先に求めて行列が正則であることを確認する。
② 逆行列を求めたらもとの行列との積をとって単位行列になることを確認する。
といったところだろう。
次回は逆行列が実際に役に立つ場面を応用編として見せようと思う。
下記に続く。




コメント