前回
の続き。
今回は行列において重要な概念である逆行列を紹介し、そこで登場するディターミナントという数について見ていく。
一般論
2つの行列\(\mathsf{A},\mathsf{B}\)があり、その積が
\begin{align}
\mathsf{AB}=\mathsf{BA}=\mathsf{I}=\begin{pmatrix}1&0&\cdots&0\\0&1&\cdots&0\\ \vdots & \vdots & \ddots &\vdots\\ 0&0&\cdots&1\end{pmatrix}
\end{align}
を満たすとき、行列\(\mathsf{B}\)は行列\(\mathsf{A}\)の逆行列であるといい、\(\mathsf{B}=\mathsf{A}^{-1}\)と書く(逆もまた然り)。
ここで導入した行列\(\mathsf{I}\)は単位行列と呼ばれ、対角成分(\(a_{i,i}\))が全て1で、それ以外はすべて0という行列だ。
単位行列は数の掛け算でいうところの1に当たる行列で、行と列の数が同数の行列に対して積を取ると、元の行列に戻る性質を持つ。
以下、2次の正方行列と3次の正方行列の逆行列の求め方を見ていく。
2次の正方行列の逆行列
まずは2次の正方行列の逆行列の求め方だが、以下のようにして求める。
2次の正方行列の逆行列の求め方
① もとの行列の1,1成分と2,2成分の積から、1,2成分と2,1成分の積を引いた数を求める。
下図のように、たすきがけに掛け算をすると覚えておくと良い。
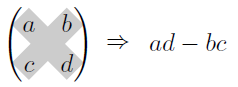
② もとの行列の1,1成分と2,2成分を入れ替え、1,2成分と2,1成分の符号を反転させた行列を作る。
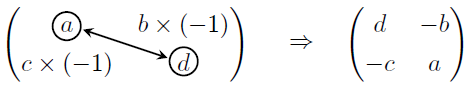
③ ①で求めた数を②で求めた行列に掛ければ、それが元の行列の逆行列になる。
\begin{align}
\begin{pmatrix}a&b\\c&d\end{pmatrix}^{-1}=\frac{1}{ad-bc}\begin{pmatrix}d&-b\\-c&a\end{pmatrix}
\end{align}
上の表式を見て気づいた人もいるかと思うが、行列によっては逆行列が存在しない場合がある。
それは、係数部分の分母\(ad-bc\)が0になるときだ。
この\(ad-bc\)がディターミナントと呼ばれる数であり、行列\(\mathsf{A}\)のディターミナントは\(\text{det}[\mathsf{A}]\)と表す。
ディターミナントが0でないとき、その行列は正則であるという。
練習問題
次の行列\(\mathsf{A},\mathsf{B}\)が正則か否かを調べた上で、その逆行列を求めよ。
\begin{align}
\mathsf{A}=\begin{pmatrix}2&5\\3&8\end{pmatrix}\qquad\qquad\mathsf{B}=\begin{pmatrix}3&2\\6&4\end{pmatrix}
\end{align}
解答
まず行列\(\mathsf{A}\)について、ディターミナントを計算すると\(\text{det}[\mathsf{A}]=(2\times8)-(5\times3)=16-15=1\)となり、行列\(\mathsf{A}\)は正則であるから逆行列が存在する。
よって上記の求め方に従って逆行列を求めると、
\begin{align}
\mathsf{A}^{-1}=\frac{1}{\text{det}[\mathsf{A}]}\begin{pmatrix}8&-5\\-3&2\end{pmatrix}=\begin{pmatrix}8&-5\\-3&2\end{pmatrix}
\end{align}
となる。
続いて行列\(\mathsf{B}\)だが、ディターミナントを計算すると\(\text{det}[\mathsf{B}]=(3\times4)-(2\times6)=12-12=0\)となり、行列\(\mathsf{B}\)は正則ではない。
よって、行列\(\mathsf{B}\)には逆行列が存在しないことがわかる。
下記に続く。




コメント