前回まで、物理の問題を解く上で欠かせない微分方程式を扱ってきたが、今回から扱うテーマを大きく変える。
行列は、最初こそ覚えることも多く扱いづらいが、使いこなせるようになると複雑な物理系の問題を解く際に大活躍する。
ここでは導入を必要最低限に抑えた上で、物理の問題で行列を使いこなせるようになることを目指す。
そもそも「行列」とは?
一般に「行列」というと人が並ぶ様子をイメージすると思うが、数学での行列はそのイメージとは異なる。
具体例を見せると、行列とは下記のようなものだ。
\begin{align}
\pmatrix{1 & 2& 3\\4&5&6\\7&8&9} \tag{1}\label{mat1}
\end{align}
書き方としては、縦横に数を並べてカッコで括るだけである。
横の数字群を「行」、縦の数字群を「列」とよび、2つを合わせて行列と呼ぶ。
(\ref{mat1})は特に縦横の数字の数が同じで正方形状に並んでいるため、正方行列と呼ばれる。
今後は基本的には正方行列しか扱わないので、正方行列を単に「行列」と呼ぶことにする。
各行と各列の呼び方は、上から順に第\(i\)行、左から順に第\(j\)列となる。
例えば一番上の行\((1,2,3)\)は第1行、真ん中の列\((2,5,8)\)は第2列となる。
最初は縦横のどっちが「行」で、どっちが「列」か迷うかもしれないが、私はいつも「行には横棒2本、列には縦棒2本」と覚えている。

より一般化した書き方をすると、下記のようになる。
\begin{align}
\mathsf{A}=\pmatrix{a_{1,1} & a_{1,2}& \cdots & a_{1,d} \\ a_{2,1}& a_{2,2}&\cdots&a_{2,d}\\ \vdots & \vdots & \ddots& \vdots \\ a_{d,1}&a_{d,2}&\cdots&a_{d,d}} \tag{2}\label{mata}
\end{align}
\(a_{i,j}\)は行列\(\mathsf{A}\)の\(i\)行、\(j\)列に位置する成分であり、単に「行列\(\mathsf{A}\)の\(i,j\)成分」と呼んだりもする。
この一般化した書き方は、今後様々な定義づけをする際に利用していくので慣れておいてもらいたい。
行列の演算
(\ref{mata})と同じ要領で、行列\(\mathsf{B}\)を下記のように定義する。
\begin{align}
\mathsf{B}=\pmatrix{b_{1,1} & b_{1,2}& \cdots & b_{1,d} \\ b_{2,1}& b_{2,2}&\cdots&b_{2,d}\\ \vdots & \vdots & \ddots& \vdots \\ b_{d,1}&b_{d,2}&\cdots&b_{d,d}} \tag{3}\label{matb}
\end{align}
これら2つの行列を使って、行列の演算を詳しく見ていく。
まず、和(足し算)と差(引き算)は下記のように実行する。
行列の和
\begin{align}
\mathsf{A}+\mathsf{B}=\pmatrix{a_{1,1}+b_{1,1} & a_{1,2}+b_{1,2}& \cdots & a_{1,d}+b_{1,d} \\ a_{2,1}+b_{2,1}& a_{2,2}+b_{2,2}&\cdots&a_{2,d}+b_{2,d}\\ \vdots & \vdots & \ddots& \vdots \\ a_{d,1}+b_{d,1}&a_{d,2}+b_{d,2}&\cdots&a_{d,d}+b_{d,d}} \tag{4}\label{matpl}
\end{align}
行列の差
\begin{align}
\mathsf{A}-\mathsf{B}=\pmatrix{a_{1,1}-b_{1,1} & a_{1,2}-b_{1,2}& \cdots & a_{1,d}-b_{1,d} \\ a_{2,1}-b_{2,1}& a_{2,2}-b_{2,2}&\cdots&a_{2,d}-b_{2,d}\\ \vdots & \vdots & \ddots& \vdots \\ a_{d,1}-b_{d,1}&a_{d,2}-b_{d,2}&\cdots&a_{d,d}-b_{d,d}} \tag{5}\label{matmi}
\end{align}
やっていることは単純で、同じ成分同士で足し算、引き算を実行しているだけである。
続いて定数倍。
これも、各成分が全て同じ定数倍になるだけだ。
定数倍
\begin{align}
k\mathsf{A}=\pmatrix{ka_{1,1} & ka_{1,2}& \cdots & ka_{1,d} \\ ka_{2,1}& ka_{2,2}&\cdots&ka_{2,d}\\ \vdots & \vdots & \ddots& \vdots \\ ka_{d,1}&ka_{d,2}&\cdots&ka_{d,d}} \tag{6}\label{matkbai}
\end{align}
さて、ここからが重要。
次に見せるのは、行列の積(掛け算)だ。
今までの流れから考えると、同じ位置にある成分同士を掛け算すると思うかもしれないが、実際はそうはならない。
先に結果を示す。
行列の積
\begin{align}
\mathsf{A}\times\mathsf{B}=\mathsf{AB}=\begin{pmatrix}
\displaystyle{\sum_{k=1}^{d}a_{1,k}b_{k,1}}& \displaystyle{\sum_{k=1}^{d}a_{1,k}b_{k,2}} & \cdots & \displaystyle{\sum_{k=1}^{d}a_{1,k}b_{k,d}}\\
\displaystyle{\sum_{k=1}^{d}a_{2,k}b_{k,1}}& \displaystyle{\sum_{k=1}^{d}a_{2,k}b_{k,2}} & \cdots & \displaystyle{\sum_{k=1}^{d}a_{2,k}b_{k,d}}\\
\vdots & \vdots & \ddots & \vdots \\
\displaystyle{\sum_{k=1}^{d}a_{d,k}b_{k,1}}& \displaystyle{\sum_{k=1}^{d}a_{d,k}b_{k,2}} & \cdots & \displaystyle{\sum_{k=1}^{d}a_{d,k}b_{k,d}}\\
\end{pmatrix}
\end{align}
なんのこっちゃわからないという人もいると思うが、上の式を暗記しろとは言わないので安心してほしい。
今後は、2次の正方行列(2×2の正方行列)同士と、3次の正方行列(3×3の正方行列)同士の掛け算さえマスターできれば良い。
まずは2次の正方行列同士の掛け算を下記に示す。
\begin{align}
\begin{pmatrix}a_{1,1}&a_{1,2}\\ \,&\, \\ a_{2,1}&a_{2,2}\end{pmatrix}\times \begin{pmatrix}b_{1,1}&b_{1,2}\\ \,&\, \\ b_{2,1}&b_{2,2}\end{pmatrix}=\begin{pmatrix}a_{1,1}b_{1,1}+a_{1,2}b_{2,1} & a_{1,1}b_{1,2}+a_{1,2}b_{2,2} \\ \,&\, \\ a_{2,1}b_{1,1}+a_{2,2}b_{2,1} & a_{2,1}b_{1,2}+a_{2,2}b_{2,2} \end{pmatrix}
\end{align}
上の式を暗記できれば事足りるだろうが、私自身はこの式を暗記して計算してはいない。
どのように計算しているかというと、こんな具合。
① 行列\(\mathsf{A}\)の第1行と行列\(\mathsf{B}\)の第1列に注目する。
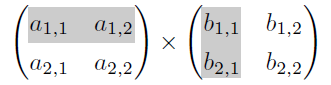
② 行列\(\mathsf{A}\)の第1行を左から右へ、行列\(\mathsf{B}\)の第1列を上から下へ読み上げ、重なる成分を乗算する。
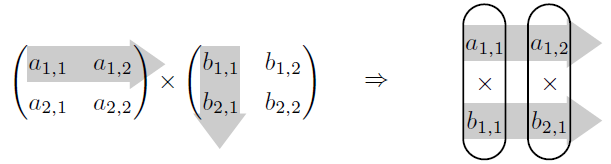
③ 乗算したものを足し上げて、その結果を行列の第1行と第1列が重なる1,1成分に置く。
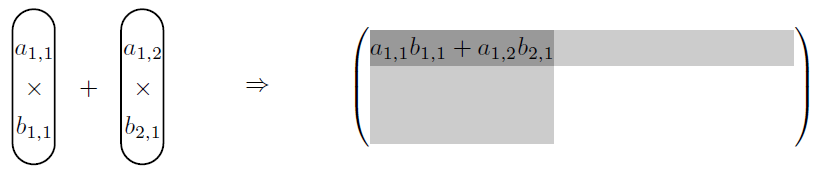
④ 答えのその他のi,j成分(1,2成分、2,1成分、2,2成分)についても、行列\(\mathsf{A}\)のi行、行列\(\mathsf{B}\)のj列で同様の計算をして埋める。
3次の正方行列同士の掛け算も考え方は同じだ。
(1つの成分に対して掛け算が3つに増えるので面倒ではあるが。)
またこれを見て気づいた人もいるかと思うが、行列の積は交換法則が成り立たない。
基本的には\(\mathsf{AB}\neq \mathsf{BA}\)であり、等号が成立するのは稀であると思っていてよい。
具体例
ここで、行列の掛け算の具体例を示しておく。
まず問題だけ示すので、最初は自分で計算してみると良いだろう。
問題:次の計算をせよ。
\begin{align}
&(1)\quad\begin{pmatrix}2 & 5 \\ -4& 9\end{pmatrix}\times \begin{pmatrix}-8 & -9 \\ 3&-7\end{pmatrix}\\
\,\\
&(2)\quad\begin{pmatrix}3&-8&-5\\-9&1&2\\1&4&6\end{pmatrix}\times\begin{pmatrix}2&5&-9\\-3&-8&4\\7&1&-4\end{pmatrix}
\end{align}
解答
\begin{align}
&(1)\quad &&\begin{pmatrix}2 & 5 \\ -4& 9\end{pmatrix}\times \begin{pmatrix}-8 & -9 \\ 3&-7\end{pmatrix}\\
& &&=\begin{pmatrix}\{2\times(-8)\}+(5\times 3)&\{2\times (-9)\}+\{5\times(-7)\}\\ \{(-4)\times(-8)\}+(9\times 3)& \{(-4)\times (-9)\}+\{9\times(-7)\} \end{pmatrix} \\
& &&=\begin{pmatrix}-1 & -53 \\ 59 & -27\end{pmatrix}\\
\,\\
&(2)\quad&& \begin{pmatrix}3&-8&-5\\-9&1&2\\1&4&6\end{pmatrix}\times\begin{pmatrix}2&5&-9\\-3&-8&4\\7&1&-4\end{pmatrix} \\
& &&=\begin{pmatrix}6+24-35 & 15+64-5 &-27-32+20 \\ -18-3+14&-45-8+2&81+4-8\\2-12+42&5-32+6&-9+16-24\end{pmatrix}\\
& &&=\begin{pmatrix}-5&74&-39\\-7&-51&77\\32&-21&-17\end{pmatrix}
\end{align}
次回予告
今回は行列とは何者か、そして行列の基本演算を見てきた。
次回は行列特有の量であるディターミナントと逆行列、そして種々の特別な行列について見ていく予定だ。
そこまでいけば、対角化の話に持っていけると思う。
END
※追記
逆行列とディターミナントの記事を書いた。





コメント