前回
にて剛体がつりあっているときの力の求め方を見てきた。
今回はその応用として、棒がすべらない条件を求める問題を扱っていく。
例題1
例題1
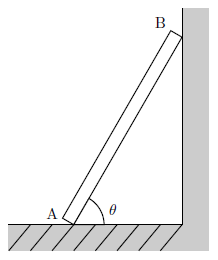
右図のように、なめらかな壁と摩擦のある床に、一様な太さの棒を立てかける。
ただし、棒と床がなす角を\(\theta\)、棒の質量を\(m\)、棒の長さを\(L\)、重力加速度の大きさを\(g\)、棒と床との間の静止摩擦係数を\(\mu\)とする。
(1) 棒が倒れないための\(\theta\)の条件を、\(\tan{\theta}\)を用いた式で表せ。
(2) 棒の下端Aから距離\(\ell\)の位置に、質量\(M\)の人が登った状況を考える。このとき、棒が倒れないための\(\theta\)の条件を求めよ。ただし、\(\ell>L/2\)とする。
解説
(1)
棒が受ける力は、重力\(mg\)、壁からの垂直抗力、水平面からの垂直抗力、水平面からの静止摩擦力の4つである。
壁からの垂直抗力の大きさを\(T\)、水平面からの垂直抗力の大きさを\(R\)、水平面からの静止摩擦力の大きさを\(F\)とすると、棒にかかる力のつりあいと、力のモーメントのつりあいからそれぞれ
\begin{gather}
R=mg \label{1-1-1}\tag{1}\\
T=F=\frac{mg}{2\tan\theta} \label{1-1-2}\tag{2}
\end{gather}
と求められる。
棒が静止し続けるためには、水平面からの静止摩擦力\(F\)が最大摩擦力\(F_{0}\)を超えなければ良い。
\begin{align}
F\leq F_{0} \label{1-1-3}\tag{3}
\end{align}
最大摩擦力の大きさは、静止摩擦係数と摩擦面(今回は床)からの垂直抗力の大きさの積で表せられるため
\begin{align}
F_{0}=\mu R=\mu mg \label{1-1-4}\tag{4}
\end{align}
となる。
よって(\ref{1-1-3})に(\ref{1-1-2})と(\ref{1-1-4})を代入すると
\begin{align}
\frac{mg}{2\tan\theta}\leq \mu mg\quad\therefore\boxed{\tan\theta \geq \frac{1}{2\mu}}
\end{align}
となり、\(\tan\theta\)の範囲を求めることが出来る。
(2)
壁に立てかけた棒に人が登ったらどうなるかという問題。
一見難しそうに感じるが、やることは至極単純で、力を1つ加えて前問と同じことを繰り返すだけである。
棒が受ける力は、重力\(mg\)、壁からの垂直抗力、水平面からの垂直抗力、水平面からの静止摩擦力、人の重力\(Mg\)の5つである。
壁からの垂直抗力の大きさを\(T’\)、水平面からの垂直抗力の大きさを\(R’\)、水平面からの静止摩擦力の大きさを\(F’\)とすると、棒にかかる力のつりあいと、力のモーメントのつりあいからそれぞれ
\begin{gather}
R’=(m+M)g \label{2-1-1}\tag{5}\\
T’=F’=\frac{g(mL+2M\ell)}{2L\tan\theta} \label{2-1-2}\tag{6}
\end{gather}
と求められる。
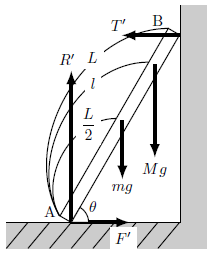
右向き、鉛直上向きを正とする。
力を全て書き出すと、図a1のようになる。
棒の下端Aから長さ\(\ell\)の位置に質量\(M\)の人が登ったため、その位置に人による重力\(Mg\)が棒にかかることに注意。
ここで力のつりあいの式を立てる。
まず、水平方向の力のつりあいの式は次のようになる。
\begin{gather}
(+F’)+(-T’)=0 \\
\therefore F’-T’=0 \label{for.2.8}\tag{a1}
\end{gather}
さらに図a1より鉛直方向の力のつりあいの式は次のようになる。
\begin{gather}
(+R’)+(-mg)+(-Mg)=0 \\
\therefore R’-mg-Mg=0 \label{for.2.9}\tag{a2}
\end{gather}
続いて、力のモーメントのつりあいの式を立てる。
今回は回転軸が指定されていないが、剛体がつりあっているときは回転軸を任意に取れるため、点Aを回転軸にとることにする。
よって図a2より力のモーメントのつりあいの式は次のようになる。
(\(R’,\,F’\)は作用線上に回転軸Aがあるので省略。)
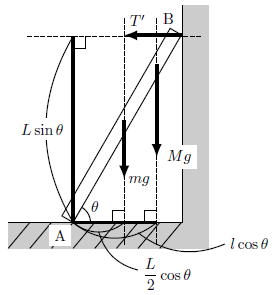
\begin{gather}
\left(-mg\times{\frac{L}{2}\cos{\theta}}\right)+(-Mg\times{\ell}\cos\theta)+(T’\times L\sin{\theta})=0 \\
\therefore T’L\sin\theta-\frac{mgL\cos\theta}{2}-Mg\ell\cos\theta=0 \label{for.2.10}\tag{a3}
\end{gather}
(\ref{for.2.8})~(\ref{for.2.10})を連立方程式とみなして解く。
まず(\ref{for.2.9})より、
\begin{align}
R’=(m+M)g \label{for.2.11}\tag{a4}
\end{align}
となる。
続いて式(\ref{for.2.10})より、
\begin{gather}
T’L\sin\theta=\frac{g\cos\theta(mL+2M\ell)}{2} \\
\therefore T’=\frac{g(mL+2M\ell)}{2L\tan\theta}\quad\left(\displaystyle{\tan\theta=\frac{\sin\theta}{\cos\theta}}\text{より}\right) \label{for.2.12}\tag{a5}
\end{gather}
となる。
そして(\ref{for.2.12})を(\ref{for.2.8})に代入すると、次のようになる。
\begin{align}
F’-\frac{g(mL+2M\ell)}{2L\tan\theta}=0 \qquad \therefore F’=\frac{g(mL+2M\ell)}{2L\tan\theta} \label{for.2.13}\tag{a6}
\end{align}
前回と同様、棒が倒れないためには、棒が床から受ける摩擦力の大きさ\(F’\)が、最大摩擦力の大きさ\(F_{0′}=\mu{R’}\)以下であればよい。すなわち、
\begin{align}
F’\leqq\mu{R’} \label{for.2.14}\tag{7}
\end{align}
となればよい。
よって、この(\ref{for.2.14})にさきほど求めた\(F’,\, R’\)を代入して整理すれば、答えとなる\(\theta\)の条件が次のように得られる。
\begin{align}
\frac{g(mL+2M\ell)}{2L\tan\theta}\leq\mu{(m+M)g} \quad \therefore\boxed{\tan\theta\geq\frac{mL+2M\ell}{2\mu{L}(m+M)}}
\end{align}
例題2
例題2
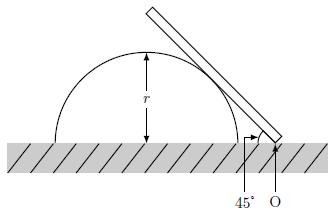
右図のように、水平面上に固定された半径\(r[\text{m}]\)のなめらかな半円柱に、長さ\(L[\text{m}]\)、質量\(m[\text{kg}]\)の太さと密度の一様な棒が、水平面と\(45\text{°}\)の角度で立てかけてある。
このとき、平面と\(45\text{°}\)で立てかけることができる、棒の長さ\(L\)の最大値を求めよ。
ただし重力加速度の大きさを\(g[\text{m/s}^{2}]\)とする。
解説
棒の長さを長くしていったとき、どの長さまでいくと棒がずり落ちてしまうのかを求めよという問題。
この問題も、前問と同様に最大摩擦力を利用する。
棒が受ける力は、重力\(mg\)、半円柱からの垂直抗力、水平面からの垂直抗力、水平面からの静止摩擦力の4つである。
半円柱からの垂直抗力の大きさを\(T[\text{N}]\)、水平面からの垂直抗力の大きさを\(R[\text{N}]\)、水平面からの摩擦力の大きさを\(F[\text{N}]\)とすると、棒にかかる力のつりあいと、力のモーメントのつりあいからそれぞれ
\begin{gather}
T=\frac{\sqrt{2}mgL}{4r}\,[\text{N}]\label{2-1}\tag{8}\\
F=\frac{mgL}{4r}\,[\text{N}]\label{2-2}\tag{9}\\
R=mg\left(1-\frac{L}{4r}\right)\,[\text{N}]\label{2-3}\tag{10}
\end{gather}
と求められる。
棒が滑らないためには、棒が水平面から受ける受ける摩擦力の大きさ\(F\,[\text{N}]\)が、最大摩擦力の大きさ\(F_{0}=\mu{R}\,[\text{N}]\)以下であればよい。
すなわち、
\begin{align}
F\leq\mu{R} \label{for.3.7}\tag{11}
\end{align}
となればよい。
よって、この式(\ref{for.3.7})にさきほど求めた\(F\,[\text{N}],\,R\,[\text{N}]\)を代入して整理すると、
\begin{align}
\frac{mgL}{4r}\leqq\mu mg\left(1-\frac{L}{4r}\right) \qquad \therefore L\leqq\frac{4\mu}{1+\mu}r\,[\mathrm{m}] \label{for.3.8}\tag{12}
\end{align}
となる。
すなわち、棒の長さが\(4\mu r/(1+\mu)\,[\text{m}]\)以下であれば棒は滑り落ちないことがわかる。
よって、平面と立てかけることができる、棒の長さ\(L\,[\text{m}]\)の最大値\(L_{\mathrm{max}}\,[\text{m}]\)は次のようになる。
\begin{align}
\boxed{L_{\mathrm{max}}=\frac{4\mu}{1+\mu}r\,\mathrm{[m]}}
\end{align}
終わりに
剛体がすべらない条件を求める問題に並んで頻出なのが、剛体が転倒しない条件を求める問題である。
転倒しない条件を求める問題では、剛体の大きさを考慮に入れる場合が多く複雑になってくる。
問題のネタはあるので時間があるときに記事にしようと思う。
END





コメント