アナログ回路の勉強を進めていくと、交流の複素数表示に必ず出くわす。
何のために複素数を用いるのか、今までその意味を自分が納得できるレベルまで理解しきれていなかった。
だが最近になってようやく、計算を楽にするために意図的に定義して導入されたものだと認識できた。
確かにこれを知っているのと知らないのとでは計算負荷が段違いだ。
本記事では複素数表示の導入によってどれほど計算負荷が変わってくるか、例題も交えながら示していく。
複素数の計算
本題に入る前に、複素数の計算の復習をしておく。
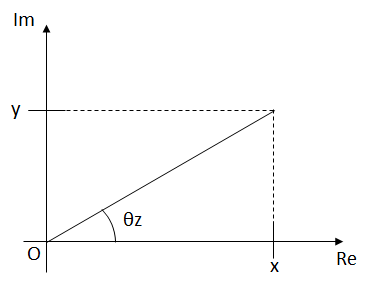
虚数単位を\(j\)とし、複素数\(z=x+jy\)の絶対値を\(|z|\)、偏角を\(\theta_{z}\)とすると、
\begin{align}
|z|=\sqrt{x^{2}+y^{2}},\quad \theta_{z}=\tan^{-1}\frac{y}{x} \tag{1}
\end{align}
となる。
すなわち、絶対値は実部と虚部の二乗和の平方根、偏角は虚部を実部で割ったものの\(\tan^{-1}\)を取ればよい。
ここで、複素数\(r=p+jq\)の絶対値を\(|r|\)、偏角を\(\theta_{r}\)とすると、複素数\(z\)との積\(rz\)の絶対値\(|rz|\)と偏角\(\theta_{rz}\)はそれぞれ
\begin{align}
|rz|=|r||z|=\sqrt{(p^{2}+q^{2})(x^{2}+y^{2})},\quad \theta_{rz}=\theta_{r}+\theta{z}=\tan^{-1}\frac{q}{p}+\tan^{-1}\frac{y}{x} \tag{2}
\end{align}
となる。
すなわち、複素数の積を取った場合は、絶対値は互いの絶対値の積、偏角は互いの偏角の和を取ればよい。
また、複素数\(r\)を複素数\(z\)で割った商\(r/z\)の絶対値\(|r/z|\)と偏角\(\theta_{r/z}\)はそれぞれ
\begin{align}
|r/z|=\frac{|r|}{|z|}=\sqrt{\displaystyle{\frac{p^{2}+q^{2}}{x^{2}+y^{2}}}},\quad\theta_{r/z}=\theta_{r}-\theta_{z}=\tan^{-1}\frac{q}{p}-\tan^{-1}\frac{y}{x} \tag{3}
\end{align}
となる。
すなわち、複素数の商を取った場合は、絶対値は互いの絶対値の商、偏角は互いの偏角の差を取ればよい。
瞬時値
ある回路に周波数\(\omega\)の正弦波交流を印加することを考える。
ある時間\(t\)での電圧を\(v(t)\)、電流を\(i(t)\)とする。
このとき、\(v(t)\)の実効値を\(|V|\)、位相を\(\theta_{v}\)、\(i(t)\)の実効値を\(|I|\)、位相を\(\theta_{i}\)とすると、\(v(t),i(t)\)はそれぞれ
\begin{align}
&v(t)=\sqrt{2}\,|V|\sin(\omega t+\theta_{v}) \tag{4}\label{v瞬時}\\
&i(t)=\sqrt{2}\,|I|\sin(\omega t+\theta_{i}) \tag{5}\label{i瞬時}
\end{align}
と書ける。
(\ref{v瞬時})と(\ref{i瞬時})はいずれも時間\(t\)における瞬間的な電圧値、電流値を表している
これを瞬時値と呼ぶ。
この瞬時値における、抵抗、コイル、コンデンサの電流-電圧特性をまとめると、表1のようになる。
| 抵抗\(R\) | コイル\(L\) | コンデンサ\(C\) | |
| 瞬時値\(v(t)=\) | \(Ri(t)\) | \(\displaystyle{L\frac{d}{dt}i(t)}\) | \(\displaystyle{\frac{1}{C}\int i(t)\, dt}\) |
| 瞬時値\(i(t)=\) | \(\displaystyle{\frac{v(t)}{R}}\) | \(\displaystyle{\frac{1}{L}\int v(t)\, dt}\) | \(\displaystyle{C\frac{d}{dt}v(t)}\) |
表1を見るとわかるように、瞬時値を用いて特性を調べるには微積分の計算が不可避であり、往々にして面倒なことが多い。
そのため実際の設計時の計算では、瞬時値を用いることはまずない。
ではどうやって計算するか?
ここで登場するのが、正弦波交流の複素数表示である。
正弦波交流の複素数表示
先に結果だけ見せると、虚数単位を\(j\)として(\ref{v瞬時})と(\ref{i瞬時})の複素数表示は下式のようになる。
正弦波交流の複素数表示
\begin{align}
&V=|V|e^{j\theta_{v}} \tag{6}\label{v複素}\\
&I=|I|e^{j\theta_{i}} \tag{7}\label{i複素}
\end{align}

ちょっと待て、\(\sqrt{2}\)と\(\omega t\)が消えているじゃないか。
と思うだろう。
確かにその通りで、(\ref{v瞬時})と(\ref{i瞬時})の複素数表示は素直に書くなら
\begin{align}
&V=\sqrt{2}|V|e^{j(\omega t+\theta_{v})} \tag{8}\label{v複素2}\\
&I=\sqrt{2}|I|e^{j(\omega t+\theta_{i})} \tag{9}\label{i複素2}
\end{align}
となるはずだ。
だが\(\sqrt{2}\)と\(e^{j\omega t}\)は\(V\)と\(I\)の共通因子であり、基本的には計算を進める過程でこの2つの因子は消えてしまう。
よって複素数表示を利用する計算では、\(\sqrt{2}\)と\(\omega t\)があっても無くても良い。
無くても良いものなら消して簡素化してしまった方が楽だ。
ということで、実務上は(\ref{v複素})と(\ref{i複素})が正弦波交流の複素数表示として計算に用いられている。
複素数表示がもたらす最大の恩恵として、素子の電流-電圧特性計算の各段な簡便化が挙げられる。
複素数表示における、抵抗、コイル、コンデンサの電流-電圧特性をまとめると、表2のようになる。
| 抵抗\(R\) | コイル\(L\) | コンデンサ\(C\) | |
| 瞬時値\(V=\) | \(RI\) | \(j\omega LI\) | \(\displaystyle{\frac{I}{j\omega C}}\) |
| 瞬時値\(I=\) | \(\displaystyle{\frac{V}{R}}\) | \(\displaystyle{\frac{V}{j\omega L}}\) | \(j\omega CV\) |
複素数表示を用いる場合では、四則演算ですべて完結している。
微積分が不可欠となる瞬時値を用いる場合と比較して、計算がかなり楽になっていることがわかると思う。
俄かには信じられないと思うので、例題を使って実感してもらうことにする。
例題
例題
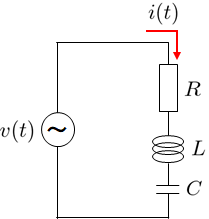
抵抗\(R\)、コイル\(L\)、コンデンサ\(C\)を直列に接続したRLC直列回路に正弦波交流\(v(t)=\sqrt{2}\,|V|\sin(\omega t+\theta_{v})\)を印加する。
このとき、回路に流れる電流\(i(t)\)の実効値\(|I|\)と位相\(\theta_{i}\)を、以下の2通りの方法で求めよ。
ただし電流の瞬時値は\(i(t)=\sqrt{2}\,|I|\sin(\omega t+\theta_{i})\)とせよ。
(1) 瞬時値から直接求める方法
(2) 複素表示を利用する方法
解答
(1)
\(v(t)\)と\(i(t)\)の間には、キルヒホッフの第2法則と各素子の電流-電圧特性より次式が成立する。
\begin{align}
v(t)=Ri(t)+L\frac{d}{dt}i(t)+\frac{1}{C}\int i(t)\,dt \tag{8}\label{瞬時RLC}
\end{align}
(\ref{瞬時RLC})の右辺に\(v(t)=\sqrt{2}\,|V|\sin(\omega t+\theta_{v})\)および\(i(t)=\sqrt{2}\,|I|\sin(\omega t+\theta_{i})\)を代入して整理すると、
\begin{align}
|V|\sin(\omega t+\theta_{v})&=R|I|\sin(\omega t+\theta_{i})+L\frac{d}{dt}|I|\sin(\omega t+\theta_{i})+\frac{1}{C}\int |I|\sin(\omega t+\theta_{i})\,dt \notag \\
&=R|I|\sin(\omega t+\theta_{i})+\omega L|I|\cos(\omega t+\theta_{i})-\frac{|I|}{\omega C}\cos(\omega t+\theta_{i}) \notag \\
&=R|I|\sin(\omega t+\theta_{i})+|I|\left(\omega L-\frac{1}{\omega C}\right)\cos(\omega t+\theta_{i}) \notag \\
&=|I|\sqrt{R^{2}+\left(\displaystyle{\omega L-\frac{1}{\omega C}}\right)^{2}}\,\left\{\frac{R}{\sqrt{R^{2}+\left(\omega L-\frac{1}{\omega C}\right)^{2}}}\sin(\omega t+\theta_{i})\right. \\
&\quad\left.+\frac{\omega L-\frac{1}{\omega C}}{\sqrt{R^{2}+\left(\omega L-\frac{1}{\omega C}\right)^{2}}}\cos(\omega t+\theta_{i})\right\}\notag \\
&=|I|\sqrt{R^{2}+\left(\displaystyle{\omega L-\frac{1}{\omega C}}\right)^{2}}\,\left\{\sin(\omega t+\theta_{i})\cos\left(\tan^{-1}\frac{\omega L-\frac{1}{\omega C}}{R}\right)\right. \\
&\quad\left.+\cos(\omega t+\theta_{i})\sin\left(\tan^{-1}\frac{\omega L-\frac{1}{\omega C}}{R}\right)\right\} \notag \\
&=|I|\sqrt{R^{2}+\left(\displaystyle{\omega L-\frac{1}{\omega C}}\right)^{2}}\,\sin\left(\omega t+\theta_{i}+\tan^{-1}\frac{\omega L-\frac{1}{\omega C}}{R}\right) \tag{9}\label{瞬時RLC2}
\end{align}
となる。
よって(\ref{瞬時RLC2})の左辺と最右辺を比較すると、
\begin{align}
\begin{cases}
|V|=|I|\sqrt{R^{2}+\left(\displaystyle{\omega L-\frac{1}{\omega C}}\right)^{2}} \\ \\
\displaystyle{\theta_{v}=\theta_{i}+\tan^{-1}\frac{\omega L-\frac{1}{\omega C}}{R}} \tag{10}\label{瞬時RLC3}
\end{cases}
\end{align}
となるため、それぞれ\(|I|,\theta_{i}\)について解けば
\begin{align}
\begin{cases}
\boxed{\displaystyle{|I|=\frac{|V|}{\sqrt{R^{2}+\left(\displaystyle{\omega L-\frac{1}{\omega C}}\right)^{2}}}}} \\ \\
\boxed{\displaystyle{\theta_{i}=\theta_{v}-\tan^{-1}\displaystyle{\frac{\omega L-\frac{1}{\omega C}}{R}}}} \tag{11}\label{瞬時RLC4}
\end{cases}
\end{align}
となる。
このように瞬時値を利用して計算を進めると、微積分、三角関数の合成が必要になり、得てして計算が煩雑になる。
(2)
では、複素表示を利用した計算はどうなるだろうか?
電圧と電流の複素表示を\(V=|V|e^{j\theta_{v}},I=|I|e^{j\theta_{i}}\)とする。
このとき\(V,I\)の間には、キルヒホッフの第2法則と各素子の電流-電圧特性より次式が成立する。
\begin{align}
V=RI+j\omega LI+\frac{I}{j\omega C} \tag{12}\label{複素RLC1}
\end{align}
(\ref{複素RLC1})を\(I\)について解くと
\begin{align}
I=\frac{V}{\displaystyle{R+j\left(\omega L-\frac{1}{\omega C}\right)}} \tag{13}
\end{align}
となるため、絶対値を取れば実効値が
\begin{align}
\boxed{|I|=\frac{|V|}{\sqrt{R^{2}+\left(\displaystyle{\omega L-\frac{1}{\omega C}}\right)^{2}}}} \tag{14}\label{複素RLC2}
\end{align}
と求まる。
また複素数\(\displaystyle{R+j\left(\omega L-\frac{1}{\omega C}\right)}\)の偏角を\(\theta_{RLC}\)とすると、偏角を計算すれば位相は
\begin{gather}
\theta_{i}=\theta_{v}-\theta_{RLC}=\theta_{v}-\tan^{-1}\frac{\omega L-\frac{1}{\omega C}}{R} \\
\boxed{\theta_{i}=\theta_{v}-\tan^{-1}\frac{\omega L-\frac{1}{\omega C}}{R}} \tag{15}
\end{gather}
と求まる。
これで終わりである。
瞬時値を利用した場合と比較して、格段に計算量が減っていることが分かると思う。
終わりに
オペアンプの選定方法など勉強してわかってきた部分も多いが、まだまだ知識不足は否めない。
ここ数年は勉強と実務の繰り返しだろうな…
幸いにも、それがネタにできてアウトプットできる場があるので、理解した部分は忘れない内になるべく早く記事にしたい。
END




コメント